Какие способами можно представить синусоидальную величину

Способы задания синусоидальных величин

Для выражения синусоидальных токов предоставляется возможность воспользоваться на выбор одним из четырех предложенных ниже способов:

1. Записью в виде уравнения, описывающего в любые произвольные моменты времени значения мгновенных величин тока: i=I_msin(ωt+Ψ); 2. Изображениями волновых диаграмм; 3. Представлением векторными выражениями; 4. Преобразованиями комплексными числами.

Между перечисленными способами существует взаимосвязь, позволяющая делать переходы из одного из них в другие с использованием доступных математических преобразований.

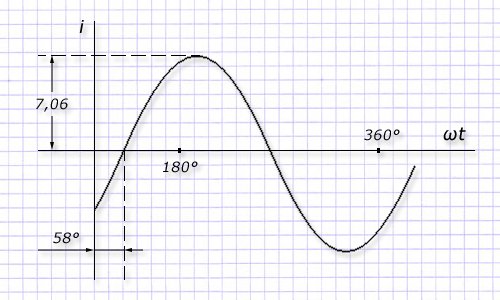
На графике ниже приведен пример представления мгновенного выражения синусоиды:

Данный пример может быть доступно описан следующими выражениями:

Пример изображения графиком волновой диаграммы для синусоиды тока:

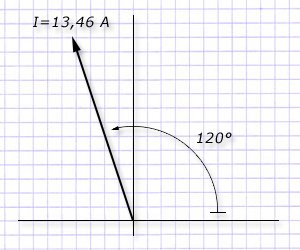
Пример векторного представления:

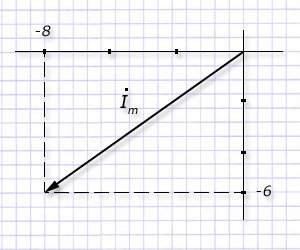
Пример представления комплексным числом:

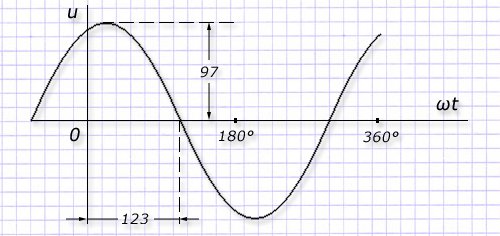
Для отсчета начальной диаграммы в последнем случае будет удобным использование не 123 угловых градуса, как демонстрирует график, а использовать угол сдвига начала синусоиды.

При таком представлении значение для начальной фазы начинается как ближайшая от начала координат точка, в которой переходит синусоида через нулевое значение амплитуды.

В данном примере это угол 56°, при смещении синусоиды влево от нуля, как в данном случае, начальная фаза будет иметь положительное значение.

Источник

Какие способами можно представить синусоидальную величину

Синусоидальные ЭДС, напряжения и токи можно изображать графически в виде соответствующих синусоид, такие графики в электротехнике называют волновыми диаграммами (см. рис. 13).

Обычно на одной волновой диаграмме изображают несколько синусоид переменных величин (напряжений, токов), относящихся к одной и той же цепи. Для оценки их взаимного расположения вдоль оси абсцисс вводится разность их начальных фаз, называемая фазовым сдвигом. Чаще всего встречается фазовый сдвиг между током и напряжением.

Если фи>0 , то говорят, что напряжение опережает ток по фазе, при фи напряжение отстает по фазе от тока, при фи=0 напряжение и ток совпадают по фазе, а если фи=П , то напряжение и ток находятся в противофазе.

Волновые диаграммы не всегда удобны для исследования, особенно при сложных разветвленных цепях. Проще в этом случае изображать синусоидальные величины вращающимися векторами. Изобразим вращающийся вектор, соответствующий току:

Длина отрезка ОА в принятом масштабе равна амплитуде тока . Проекция вектора на ось ординат (ОВ) равна мгновенному значению тока в момент времени . При вращении вектора в положительном направлении (т.е. против часовой стрелки) с угловой скоростью в любой момент времени его проекция на ось ординат будет равна соответствующему мгновенному значению тока:

Любой вектор на плоскости, проведенный из начала координат и изображающий значение ЭДС, напряжения или тока, однозначно определяется точкой, соответствующей концу этого вектора (точка на рисунке).

Комплексное число (соответствующее точке ) имеет вещественную (ОС) и мнимую (ОВ) составляющие на комплексной плоскости.

Перевод комплексных чисел из одной формы в другую можно производить по следующим формулам:

Для напряжения и тока аналогично.

При расчетах цепей синусоидального тока целесообразно перейти от гармонических функций времени к их изображениям в комплексной форме и производить все расчеты, используя комплексные числа. Конечный результат может быть представлен снова в виде синусоидальной функции времени.

Источник

Способы изображения синусоидальных величин

1. Графическое изображение синусоидальных величин.

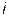
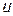
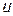
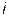
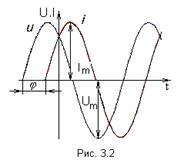Для сравнения электрических величин, изменяющихся по синусоидальному закону, необходимо знать разность их начальных фаз. Если, например, на каком — либо участке ток и напряжение имеют одинаковые начальные фазы, говорят, что они совпадают по фазе. Если график изменения во времени напряжения на каком — либо участке цепи пересекает координату времени t раньше графика тока , то говорят, что напряжение по времени опережает ток.

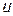
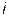
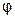
На рис. 3.2 для заданного элемента цепи представлены графики изменения во времени двух электрических величин: напряжения и тока . Из этих двух графиков видно, что они сдвинуты по фазе друг относительно друга на угол .

2. Векторное изображение синусоидальных величин.

При гармоническом изменении синусоидальной величины постоянной остаётся амплитуда. Этим можно воспользоваться для определения мгновенного значения электрической величины, не рассматривая графика её зависимости от времени.

Синусоидальную функцию времени можно изобразить вектором, равным амплитуде данной функции, равномерно вращающимся с угловой скоростью ω. При этом начальное положение вектора определяется (для t=0) его начальной фазой .

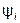
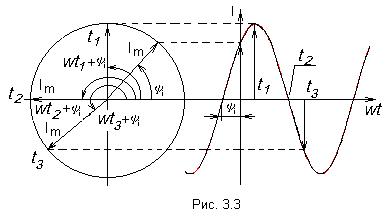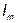
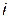
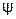
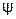
На рис. 3.3 показаны вращающийся вектор тока и график изменения тока во времени.

При изображении синусоидальной Э.Д.С., напряжений и токов из начала координат проводят векторы, равные амплитудным значениям этих величин, под углом к горизонтальной оси. Положительные углы откладываются против часовой стрелки.

Если вращать вектор против часовой стрелки, то в любой момент времени он составит с горизонтальной осью угол, равный 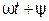. Проекция вращающегося вектора на ось ординат (ось мгновенных значений) равна мгновенному значению синусоидальной величины.

Совокупность векторов на плоскости, изображающих Э.Д.С., напряжения, токи одной частоты, называют векторной диаграммой.

При исследовании установившихся режимов векторы неподвижны, их длина равна действующим значениям электрических величин.

С помощью векторов можно производить геометрическое суммирование электрических величин.

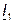
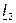
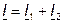
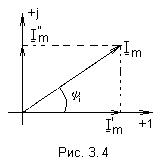Так, на рис. 3.4 показаны векторы токов и , а также вектор их геометрической суммы . Углы обозначают начальные фазы токов.

Векторные диаграммы широко используются при анализе электрических цепей переменного тока.

3. Представление синусоидальных величин комплексными числами.

Синусоидально изменяющуюся электрическую величину можно представить комплексным числом и изобразить в виде вектора на комплексной плоскости с прямоугольной системой координат.

Комплексное число состоит из действительной (вещественной) и мнимой частей. По оси ординат откладывают мнимую часть комплексного числа, а ось обозначают +j; по оси абсцисс – действительную часть комплексного числа, а ось обозначают +1.

На комплексной плоскости синусоидальная величина может изображаться в виде модуля и аргумента или в виде двух составляющих вектора, направленных по действительной и мнимой осям.

Например, синусоидальный ток представляют вектором , модулем которого является значение амплитуды тока , а аргументом – начальная фаза , которую можно выражать в радианах или в градусах (рис. 3.5).

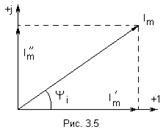
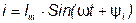
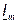
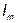
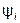
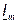
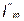
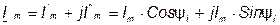
Составляющим вектора по действительной оси будет , а по мнимой — , то есть

.

Вектор 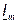называют комплексной амплитудой тока.

Обычно при расчётах пользуются действующими значениями.

При построении векторных диаграмм точно фиксируют угол сдвига между векторами, а положение их относительно осей комплексной плоскости может быть произвольным, поэтому оси можно не изображать.

При анализе электрических цепей переменного тока приходится иметь дело с умножением и делением электрических величин. В этом случае удобно пользоваться комплексами этих величин, записанными в показательной форме:

,

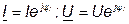
где 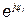— оператор поворота единичного вектора относительно оси действительных величин.

Например, при

Умножение на j означает поворот вектора на +90 градусов (в сторону, противоположную направлению движения стрелки часов).

Умножение на –j означает поворот вектора на угол –90 градусов (по часовой стрелке).

Источник