Какие нагрузки могут быть по способу приложения

Черчение

Классификация нагрузок

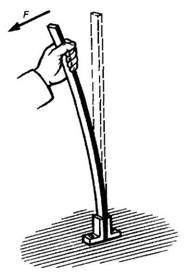
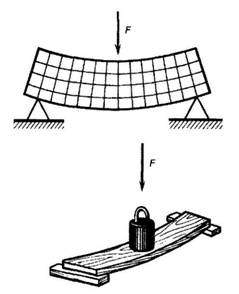
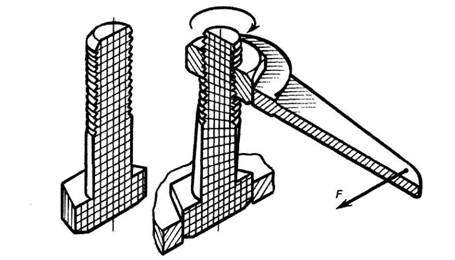
Воздействия, испытываемые стойкой от согнувшей ее руки (см. рис. 42), доской от груза (см. рис. 44), цилиндрическим стерж­нем болта при навинчивании гайки гаечным ключом (см. рис. 45) и т. д., представляют собой внешние силы или нагрузки. Силы, возникающие в местах закрепления стойки и опирания доски, называются реакциями.

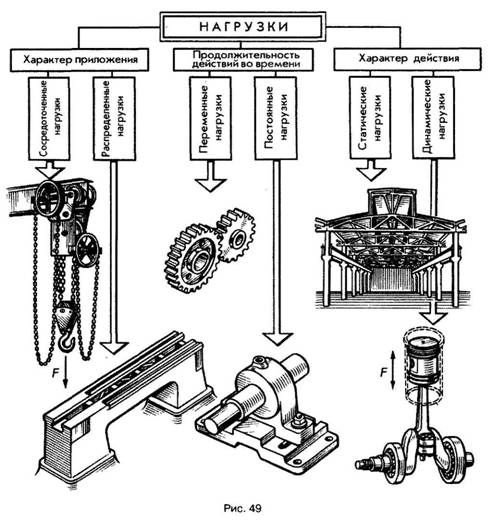
По способу приложения нагрузки делятся на сосредоточенные и распре­деленные (рис. 49).

Виды и классификация нагрузок:

Сосредоточенные нагрузки передают свое действие через,очень малые площади. Примерами таких нагрузок могут служить давление колес железнодорожного вагона на рельсы, давление тележки тали на монорельс и т. д.

Распределенные нагрузки действуют на сравнительно большой площади. Например, вес станка передается через станину на всю площадь соприкосновения с фундаментом.

По продолжительности действия принято различать постоянные и переменные нагрузки. Примером постоянной нагрузки может слу­жить давление подшипника скольжения — опоры валов и осей — и его соб­ственный вес на кронштейн.

Переменной нагрузке подвержены в основном детали механизмов пери­одического действия. Одним из таких механизмов служит зубчатая переда­ча, у которой зубья в зоне контакта смежных пар зубчатых колес испыты­вают переменную нагрузку.

По характеру действия нагрузки могут быть статическими и динамическими. Статические нагрузки почти не изменяются в тече­ние всего времени работы конструкции (например, давление ферм на опо­ры).

Динамические нагрузки действуют непродолжительное время. Их воз­никновение связано в большинстве случаев с наличием значительных уско­рений и сил инерции.

Динамические нагрузки испытывают детали машин ударного действия, таких, как прессы, молоты и т. д. Детали кривошипно-шатунных механиз­мов также испытывают во время работы значительные динамические на­грузки от изменения величины и направления скоростей, то есть наличия ускорений.

Источник

Нагрузки можно разделять по характеру действия во времени, по способу их приложения, в зависимости от назначения при экс­плуатации самого сооружения и т. д

По характеру действия во времени различают статические и динамические нагрузки. Статическую нагрузку принимают не зависящей от времени, она передается на сооружение спокойно, плавно, без толчков и вибраций, ее считают медленно возрастаю­щей от нуля до конечного значения. Динамическая нагрузка быстро меняется со временем; при расчете сооружения на динами­ческую нагрузку необходимо вводить силы инерции системы, воз­никающие при колебаниях, и динамические эффекты действия нагрузки.

По способу приложения различают сосредоточенный груз и сплошную нагрузку, распределенную по площади или по линии.

Сосредоточенный г р у з — нагрузка в виде силы, прило­женной в одной точке.

Сплошная нагрузка — распределенная непрерывно по дан­ной площади или по данной линии. Линейная сплошная нагрузка, распределенная по длине, измеряется интенсивностью ее, т. е. нагрузкой, приходящейся на единицу длины в данной точке. Поверх­ностная нагрузка измеряется нагрузкой, действующей на единицу поверхности в данной точке. Интенсивность линейно распределен­ной нагрузки измеряется в килоньютонах на метр погонной длины, а интенсивность поверхностно распределенной нагрузки — в килоньютонах на квадратный метр.

В зависимости от назначения различают постоянную, времен­ную и подвижную нагрузки. Постоянная н а г р у з к а — наг­рузка, которая постоянно действует на сооружение (собственный вес, усилия предварительного натяжения и т. п.). Временная нагрузка действует на сооружение в отдельные промежутки вре­мени, в другие же периоды она может отсутствовать (давление ветра, снега; полезная нагрузка, воспринимаемая сооружением). Подвижная нагрузка та, которая занимает различное положе­ние на сооружении (поезд, автомобиль, толпа людей). По действу­ющим нормативным документам различают основные сочетания нагрузок (состоят из постоянных и временных), дополнительные сочетания (включают и кратковременные нагрузки) и особые сочетания (сейсмические, аварийные и др.).

Классификация сооружений и их расчетных схем.

Различают сооружения плос­кие и пространственные, которые подразделяют по виду соедине­ний в узлах; по геометрическому типу элементов, составляющих сооружение; по особенностям работы сооружения и т. д.

Все сооружения, в действительности пространственные, имеют три измерения, однако в ряде случаев заменяют простран­ственные сооружения плоскими, представляющими данное прост­ранственное. Плоским сооружением называют систему, осевые линии всех элементов которой расположены в одной плоскости.

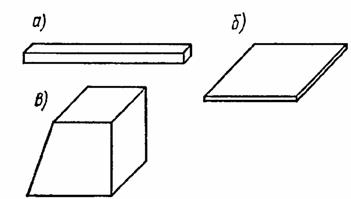
По геометрическому типу элементов сооружения могут быть стержневыми, пластинчатыми и массивными. Сооружения, состав­ленные из стержней (рис. 1.6,а), называют стержне­выми. Сооружения, предс­тавляющие собой систему пластинок (рис. 1.6,б), будем называть пластинчаты­ми. На рис. 1.6,а,б представ­лены элементы сооружений.

Рисунок 1.6 Элементы сооружений

Сооружения, три основ­ных размера которых одного и того же порядка (рис. 1.6,в), называют массивными (например, подпорная стен­ка).

По виду соединений в узлах сооружения делятся на системы с шарнирными и с жесткими узлами. В качестве при­мера первой системы можно указать ферму с шарнирными узлами, в качестве примера второй — раму с жесткими узлами.

По особенностям работы сооружений различают балочные, рам­ные, арочные и висячие системы.

Балка представляет собой прямолинейный брус, работающий на изгиб. Балка при наличии обычной горизонтальной подвижной опоры является безраспорной системой, в которой вертикальная нагрузка вызывает только вертикальные опорные реакции.

В распорной системе с криволинейным или многоугольным очер­танием оси (рама, арка) вертикальная нагрузка помимо вертикаль­ных вызывает и горизонтальные составляющие реакций — распоры.

Рамой называют стержневую систему преимущественно с жест­кими соединениями в узлах; стержни рамы работают одновременно на изгиб и осевое действие сил, причем изгибная деформация в раме преобладает.

Аркой называют криволинейный брус, закрепленный непод­вижно двумя концами. Арка со сплошной стенкой работает на осевое сжатие и изгиб.

При наличии идеально шарнирного соединения стержней во всех узлах систему называют шарнирно-стержневой фермой или просто фермой. Все стержни фермы при узловой нагрузке работают только на осевое действие сил.

Часто применяют висячие системы, в которых цепи или кабели поддерживают балочную часть. В идеальной гибкой цепи или гибком кабеле возникает только растяжение.

Сооружения можно разделить на статически определи­мые, усилия в которых определяются только с помощью одних уравнений статики, и статически неопределимые, расчет которых производится с дополнительным использованием уравне­ний связности деформаций. Применяются также методы расчета сооружений по допускаемым напряжениям и по предельным состо­яниям, методы расчета на основе точной и приближенной теорий и т. д.

Основные положения строительной механики. Основные исход­ные положения строительной механики при решении задач упру­гого расчета сооружений те же, что и сопротивления материалов:

1. Предположение об идеальной упругости и непрерывности материала, из которого состоит сооружение. Однако в специальном разделе курса рассматриваются методы расчета сооружений с уче­том развивающихся и пластических деформаций. В настоящее время ряд конструкций рассчитывается по методу предельных состояний .

2. Применение линейной связи между напряжением и деформа­цией (закон Гука). Отметим, что существуют тела, поведение кото­рых в известных границах можно считать нелинейно упругим, т. е. в которых остаточных деформаций не возникает, но зависимость между напряжением и деформацией нелинейна.

3. Применение принципа независимости действия, согласно кото­рому результат действия системы сил равен сумме результатов действия отдельных сил. Этот принцип применим только к относи­тельно жестким сооружениям, и использование его при расчете существенно гибких систем в области больших деформаций недо­пустимо.

Системы, геометрически изменяемые и неизменяемые. Сооруже­ние должно быть геометрически неизменяемым, т. е. пос­тоянно сохранять геометрическую форму, заданную при возведении. При расчете сооружений нередко используют основную схему в виде так называемой кинематической цепи — изменяемой системы. Важно знать степень свободы кинематической цепи и уметь перейти от этой цепи к неизменяемой системе путем введения соот­ветствующих связей.

Рисунок 1.7 Примеры геометрически неизменяемых и изменяемых систем

С т е п е н ь ю свободы системы называется число независимых геометрических перемещений, определяющих ее положение (например, линейных перемещений узлов). Степень сво­боды шарнирного четырехугольника по рис. 1.7, б равна единице (достаточно поставить раскос 02, чтобы обратить систему в неизме­няемую).

Формула для определения числа связей плоской стержневой системы. Рассмотрим плоские шарнирно-стержневые системы стерж­ней или дисков. Пусть задана шарнирно-стержневая система по рис.1.8, в которой шесть шарнирных узлов связаны стержнями аb, ас, аd. Ус­тановим соотношение между числом узлов системы k и числом стержней s. Под k по­нимаем число узлов без опор­ных, а под s—число стерж­ней вместе с опорными. При отсутствии всех s стерж­ней системы степень свободы будет 2k, так как степень свободы каждого узла на плоскости равна двум. При наличии связей чис­лом s = 2k система может быть неподвижна, если стержни располо­жены целесообразно. Условие неиз­меняемости системы будет s = 2k.

Для системы по рис. 1.8: s=12, k = 6.

Рисунок 1.8

В качестве примера приведем ферму, в первой панели которой имеется два раскоса, а во второй раскоса нет (рис. 1.9). Общее число стержней и узлов в данном случае s = 12; k = 6, т. е. s = 2k. Одна­ко система изменяема, так как она сводится к шарнирному четы­рехугольнику (имеем диск (неизменяемую часть) abef, который заменяем одним стержнем).

Простейшие геометрические признаки неизменяемости систем. Для окончательного суждения о неизменяемости системы необходимо провести соответствующий анализ ее геометрической структуры. Наиболее целесообразным и общим является геометрический метод исследования неизменяемости, основанный на использовании свойств гео­метрических фигур.

Первый признак геометрической неизменяемости: ферма неизме­няема, если она составлена из шарнирных треугольников (рис. 1.9), поскольку треугольник — неизменяемая геометрическая фигура.

В данном случае к исходному треугольнику abc каждый последующий узел 1, 2, 3, 4 и т. д. прикрепляется двумя стержнями, вследствие чего создается новый треугольник. Прикрепление узла 1 к узлам b и с двумя стержнями 1b и 1с, не лежащи­ми на одной прямой, равносильно соз­данию шарнирно-стержневого неизме­няемого треугольника.

Более общий признак геометричес­кой неизменяемости ферм следующий: ферма неизменяема, если каждый пос­ледующий узел прикрепляется к двум предшествующим узлам двумя стерж­нями, осевые линии которых не лежат на одной прямой. Такой структурой обладают все простейшие фермы, пред­ставляющие собой совокупность диад (диада — пара наклонных стержней, связанных общим узлом).

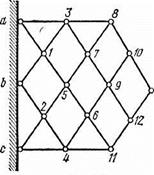
На рис. 1.10 изображена консольная ферма с ромбической решет­кой, к узлам a, b и с которой двумя стержнями каждый прикреп­ляются узлы 1, 2, 3, 4, 5, 6 и т. д.

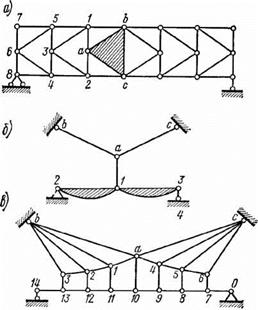
На рис. 1.11 приведен ряд ферм, образованных по указанному общему признаку. Выделен основной треугольник — геометрический базис, к которому присоединяются все остальные узлы фермы; пос­ледовательность их прикрепления отмечена цифрами.

Указанные два признака создания геометрически неизменяемых шарнирно-стержневых систем, однако, неприменимы для анализа геометрической неизменяемости любых ферм. Общим методом исследования не­изменяемости является анализ определителя системы уравнений для всех усилий в стержнях данной фермы при действии на нее про­извольной нагрузки.

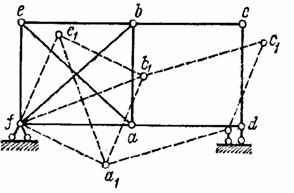
Мгновенно изменяемая система. Выше было установлено, что при прикреплении данного узла двумя стержнями осевые линии стержней не должны располагаться на одной прямой, иначе говоря, не должно находиться на одной прямой три шарнира. Случай прикрепления узла двумя стержнями аb и ас, лежащими на одной прямой (рис. 1.12, а), дает мгновенно изменяемую систему:

точка а вследствие фиксации ее положения касающимися дугами окружнос­тей радиусов аb и ас может получить бесконечно малое смещение (точка a₁). Конечное же смещение точки а возможно лишь в результате удлинения стержней; при этом система обращается в не­изменяемую, так как шарниры а, b и с уже не будут лежать на одной прямой.

Мгновенно изменяемой называют систему, которая ока­зывается изменяемой лишь в первый момент приложения соответ­ствующей нагрузки.

Дадим статическую характеристику мгновенно изменяемой системы для данного частного случая. Предположим, что стержни ab и ас не лежат на одной прямой (рис. 1.12, б); определим усилия X для случая симметричного расположения стержней. Проектируя все силы, приложенные к узлу а, на вертикальную ось, находим

При стремлении α к нулю усилие X стремится к бесконечности. При малом значении α усилие X получает конечное очень большое значение. Когда же точка а незначительно отклоняется от прямой be,в стержнях ab и ас возникают усилия, вызывающие если не разрушение, то во всяком случае значительные деформации, что сопровождается резким опасным смещением точки а.

Итак, в случае прикрепления шарнира а двумя стержнями ab и ас, лежащими на одной прямой (три шарнира а, b, с — на одной прямой), система мгновенно изменяема.

Источник