Какие могут быть измерения по способу получения информации

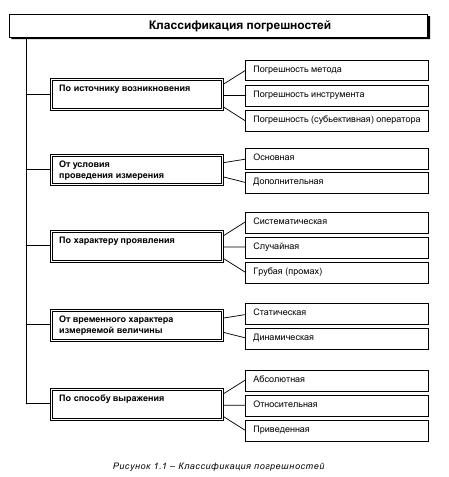
1.4. Виды измерений по метрологии

Цель измерения – получение значения этой величины в форме, наиболее удобной для использования. Классификация измерений

Содержание:

По характеристике точности

• Равноточные измерения – ряд измерений какой-либо величины, выполненных в одинаковых условиях.
• Неравноточные измерения – ряд измерений, выполненных СИ различной точности и в разных условиях.

По количеству измерительной информации

• Однократные измерения – число измерений равно числу измеряемых величин.
• Многократные измерения – минимальное число измерений величины больше трех.

По выражению результата измерений

• Абсолютные измерения — это такие, при которых используются прямое измерение одной (иногда нескольких) основной величины и физическая константа. Так, в известной формуле Эйнштейна E =mc 2 масса (m) – основная физическая величина, которая может быть измерена прямым путем (взвешиванием), а скорость света (с) – физическая константа.
• Относительные измерения — установление отношения измеряемой величины к однородной, применяемой в качестве единицы.
• Прямые измерения – непосредственное сравнение физической величины с ее мерой. Например, при определении длины предмета линейкой происходит сравнение искомой величины (количественного выражения значения длины) с мерой, т.е. линейкой.
• Косвенные измерения — искомое значение величины устанавливают по результатам прямых измерений таких величин, которые связаны с искомой определенной зависимостью.

По способу получения результатов измерений

• Совместные измерения — измерения одновременно двух или нескольких разноименных величин для нахождения зависимости между ними.
• Совокупные измерения – это проводимые одновременно измерения одноименных величин, при которых значения искомых величин находят решением системы уравнений, получаемых при измерениях этих величин в различных состояниях.

По метрологическому назначению

• Технические измерения – с помощью рабочих средств. Применяются в науке и технике, с целью контроля параметров изделий, процессов и т.д.
• Метрологические измерения – при помощи эталонов и образцовых средств измерения, с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений.

По характеру изменения измеряемой величины

Статистические измерения связаны с определением характеристик случайных процессов, звуковых сигналов, уровня шумов и т.д.

• Статические измерения — величины практически постоянны.
• Динамические измерения — величины, в процессе измерений претерпевают те или иные изменения.

Статические и динамические измерения в идеальном виде на практике редки.

Источник

Классификация измерений

Содержание

Измерения можно классифицировать разными способами.

Классификация по характеру зависимости измеряемой величины от времени

По характеру зависимости измеряемой величины от времени измерения могут быть:

• статическими (измеряемая величина постоянна в течение всего периода измерений) и
• динамическими (измеряемая величина изменяется во времени).

Примеры: статические измерения — измерение длины или массы твердого тела, динамические — измерение температуры или давления в химическом реакторе. Отметим, что химический анализ получаемого продукта реакции в большинстве случаев — это статическое измерение, поскольку концентрация определяемых веществ в пробе в ходе анализа обычно постоянна.

Классификация по способу получения результатов

По способу получения результатов измерения делятся на:

• прямые, когда искомое значение измеряемой величины находят непосредственно из опытных данных, и
• косвенные, когда значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.

Кроме того, проводят совместные измерения — одновременные измерения двух или более различных величин, осуществляемые обычно для нахождения зависимости между ними. Типичным примером совместных измерений является градуировка термопары: одновременно измеряют ЭДС термопары и температуру среды, в которую помещен ее спай.

В случае одновременных измерений нескольких одноименных величин их называют совокупными. При этом искомую величину находят, решая систему уравнений, полученных по­средством прямых измерений различных сочетаний этих величин.

Классификация по условиям, определяющим точность измерений

По условиям, определяющим точность измерений, выделяют:

• измерения максимально возможной точности, достижимой при существующем уровне техники;
• контрольно-поверочные измерения — измерения, выполняемые с помощью средств измерений и по методи­кам, гарантирующим погрешность результата с заданной вероятностью;
• технические измерения, в которых погрешность результата определяется погрешностью средств измерений.

Измерения максимально возможной точности — это главным образом измерения, выполняемые для воспроизведения единиц физических величин и для измерения физических констант. Контрольно-поверочные измерения выполняются лабораториями с целью контроля за состоянием измерительной техники, а также для проверки качества работы специализированных измерительных лабораторий (например, заводских). Эти два вида измерений являются метрологическими по своему характеру, поскольку проводятся с использованием эталонов и образцо­вых средств измерений с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений. Технические измерения — все остальные измерения, выполняемые на практике, например рутинные измерения в заводских лабораториях.

Классификация по способу выражения результатов

По способу выражения результатов измерения делятся на:

• абсолютные, основанные на прямых измерениях одной или нескольких физических величин или на использовании значений физических констант;
• относительные, когда измеряется отношение величины к одноименной величине, играющей роль единицы или принимаемой за исходную.

Результаты относительных измерений вы­ражаются либо в долях (безразмерные величины), либо в процентах.

Классификация по характеристике точности измерений

По характеристике точности измерений рассматривают:

• равноточные измерения — ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений и в одних и тех же условиях, например взятие нескольких навесок вещества на одних и тех же аналитических весах с помощью одних и тех же разновесов в одних и тех же условиях, и
• неравноточные измерения — ряд измерений какой-либо величины, выполненных различными по точности средствами измерений и (или) в разных условиях, например взятие навески одного и того же вещества на весах различной чувствительности или при различной температуре.

Классификация по числу измерений одной и той же величины в ряду измерений

По числу измерений одной и той же величины в ряду измерений последние подразделяют на:

Однократные измерения выполняют один раз, например измерение момента времени по часам или температуры раствора в условиях ее постоянства. Часто на практике этого бывает вполне достаточно.

При многократном измерении одного и того же размера физической величины результат получают на основании нескольких следующих друг за другом измерений, т.е. из ряда однократных измерений. За результат многократного измерения обычно принимают среднее арифметическое из суммы результатов отдельных измерений. Условно принято считать измерение многократным, если число отдельных измерений больше или равно 4. В этом случае данные ряда измерений могут быть обработаны методами математической статистики.

Ссылка на источник

01.09.2021 11:24:07 | Автор статьи: Усачёва Вера

Источник

Классификация измерений

Дата добавления: 2014-05-22 ; просмотров: 2442 ; Нарушение авторских прав

Классификацию измерений можно проводить различными способами.

1. По способу получения информации:

1) Прямые измерения — измерения, при которых искомое значение величины находят непосредственно (путем сравнения с мерой этой величины).

2) Косвенные измерения – определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.

3) Совокупные измерения — проводимые одновременно измерения нескольких однородных величин, при которых искомые значения величин с определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.

Пример: измерение взаимоиндуктивности между катушками. Имеются катушки L1и L2. Для получения искомого результата сначала соединяют катушки так, чтобы их магнитные поля складывались L01 = L1 + L2 + 2M, затем катушки соединяют так, чтобы их магнитные поля вычитались L02 = L1 + L2 — 2M. Значения L1и L2получают с помощью прямых измерений. Решение уравнений для L01 и L02позволяет найти искомую величину — взаимоиндуктивности М = (L01- L02)/4, измеряемую в генри.

4) Совместные измерения — проводимые измерения двух или нескольких неодноименных величин для определения зависимости между ними.

2. По характеру изменения измеряемой величины в процессе измерений

1) Статические измерения – измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.

2) Динамические измерения — измерение изменяющейся по размеру физической величины.

3) Статистические измерения – измерения, связанные с определением характеристик случайных процессов, шумовых сигналов и др.

3. По количеству измерительной информации:

1) Однократное измерение – измерение выполненное один раз.

Примечание. Как правило не более трех раз, результат при этом усредняется. Например, при измерении плотности жидкости ареометром образуется мениск, затрудняющий снятие показаний. Мы часто прибегаем к услугам других лиц: одного, другого. Результат мы находим как среднее арифметическое.

2) Многократное измерение — измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом единичных измерений. При этом количество измерений таково, что можно применить статистические методы для обработки измерений.

Примечание. Единичное измерение не следует путать с однократным измерением. Однократное измерение является частным случаем многократного измерения. Любое измерение является совокупностью операций, включающих и оценку погрешности результата измерения. Следующие друг за другом единичные измерения не являются однократными измерениями, так как оценку результата измерения и оценку погрешности при многократных измерениях производят для всей совокупности измерений, а не в отдельности. Ранее для таких следующих друг за другом единичных измерений существовали термины «наблюдение» или «замер».

4. По отношению к основным единицам:

1) Абсолютное измерение — измерение основанное на прямых измерениях одной или нескольких основных величин и/или использовании значений физических констант.

Пример: E = mc2- измерения абсолютные, с — константа.

Контрпример: 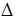р = КQ2, где р — перепад давления, Q — расход на сужающем устройстве, К — коэффициент, зависящий от параметров сужающего устройства, плотности и вязкости вещества.

2) Относительное измерение — измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.

Источник

Способы получения измерительной информации

Согласно [24] измерение физической величины – это совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.

В этом определении учтена техническая сторона (совокупность операций), раскрыта метрологическая суть измерений (сравнение с единицей) и показан гносеологический аспект (получение значения величины). В тех случаях, когда невозможно выполнить измерение (не выделена величина как физическая и не определена единица измерений этой величины) практикуется оценивание таких величин по условным шкалам.

Суть измерения заключается в сравнении. Не существует иного способа получения информации о размере ФВ, кроме как путем сравнения его с другим размером такой же физической величины, т.е. имеющей такую же размерность. Измерение суть сравнение размеров опытным путем. Сравнение размеров опытным путем является единственным способом получения измерительной информации. При этом не уточняется, каким образом происходит сравнение размеров одноименных физических величин, с по- мощью каких приспособлений или даже может быть без них. Просто утверждается, что другого способа нет.

Вариантов сравнения между собой двух размеров Qi и Qj всего три [33]:

определения числового значения q измеряемой физической величины, которое показывает, во сколько раз неизвестный размер больше размера единицы, или на сколько единиц он больше нуля.

Таким образом, последняя разновидность способа сравнения является самой информативной. Она позволяет определить значение измеряемой физической величины Q, т.е. выразить её размер в общепринятых (узаконенных) единицах в кратном или дольном отношении, и отвечает на вопрос, во сколько раз или на сколько (единиц) один размер больше (меньше) другого.

Измерение — познавательный процесс, заключающийся в сравнении путем физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения.

В практической деятельности необходимо проводить измерения различных величин, характеризующих свойства тел, веществ, явлений и процессов. Некоторые свойства проявляются только качественно, другие — количественно. Многообразные проявления (количественные или качественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае условных знаков образуют шкалы измерения этих свойств. Шкала измерений количественного свойства является шкалой физической величины.

Шкала физической величины представляет собой упорядоченную совокупность значений этой величины, принятую по соглашению на основании результатов точных измерений.

Согласно теории измерений измерение трактуется как отображение элементов эмпирической системе с отношениями (совокупность объектов, их свойств и отношений) на элементы абстрактной системы с отношениями (совокупность оценок и правил их образования), осуществляемое по определенной системе правил соотнесения эмпирической и абстрактной систем (совокупность правил и процедур оценивания).

Совокупность правил, позволяющих выполнить такое сопоставление эмпирической системы отношений в числовую систему отношений, называется шкалой.

В соответствии с логической структурой проявления свойств в теории измерений различают пять основных типов шкал измерений: две — неметрические шкалы (шкала наименований и шкала порядка) и три — метрические шкалы (шкала интервалов, отношений и абсолютные шкалы).

1.3.2. Неметрические шкалы

Шкала наименований (шкала классификации). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами физических величин. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. Условные номера в качестве имен присваиваются по следующему правилу: нельзя присваивать одно имя (число) двум разным объектам. Поскольку числа характеризуются только отношениями эквивалентности, то в них отсутствует понятие нуля, «больше» или «меньше» и единицы измерения.

Номинальное измерение является качественным измерением. Единственный факт, существенный при номинальных измерениях, заключается в том, что одинаковым характеристикам, состояниям и явлениям присваиваются одни и те же метки, а различным характеристикам — разные. Сущностью такого измерения является безусловный смысл равенства и неравенства. Процедура присвоения ограничена лишь тем, что одно имя можно присвоить лишь одному объекту (классу).

Примером номинального измерения в технических науках служит целый класс измерений, осуществляемых системами обнаружения. Эти системы конструируются так, чтобы результат их действия был двоичным. Системы пожарной сигнализации вырабатывают сигнал «пожара нет», когда температура ниже определенного значения, и сигнал «пожар», когда температура превышает это значение. В этом случае отношение в эмпирической системе для номинального измерения — тождество. Номинальное измерение не может указать, какое из событий или явлений больше или меньше. Все, что можно определить, это «случилось» или «не случилось». Если число возможных исходов больше двух, то номинальное измерение может указать, какое именно событие произошло. Например, цвет любой вещи можно определить по названию подходящего цвета в атласе цветов, предназначенном для идентификации цвета.

Кроме того, с помощью номинального измерения осуществляют классификацию, которая существует во многих разновидностях: например, с помощью диагностических средств классифицируют болезнь, также классифицируют флору, фауну, проводят контроль изделий (классификация на годные и бракованные), осуществляют сложную процедуру распознавания образов и т.д. Номинальная шкала, используемая для классификации, называется шкалой классификации. При классификации существенно лишь то, что единственное отношение в системе объектов, передаваемое шкалой классификации, — это отношение эквивалентности. Так, все годные изделия эквивалентны в том смысле, что могут быть использованы.

Шкала порядка (шкала рангов). Результат экспериментального решения неравенства (1.2) может быть представлен на шкале порядка, являющейся упорядоченной последовательностью опорных (реперных) точек, обозначаемых буквами, цифрами или символами и соответствующих размерам Q₁ — 6 ).

Особый интерес представляет группа величин с ограниченными шкалами (такие, как коэффициент полезного действия, вероятность). Их значения могут находиться только в пределах от 0 до 1, причем конечные точки этого диапазона физически как бы бесконечно удалены, недостижимы (на практике это обстоятельство вынуждает перейти к логарифмическим оценкам вблизи этих точек).

Логарифмическая величина представляет собой логарифм безразмерного отношения двух одноименных физических величин. Логарифмические величины применяют для выражения уровня звукового давления, усиления, ослабления, выражения частотного интервала и т.д. Единицей логарифмической величины является бел (Б), определяемый соотношением 1Б=lg(P2/P1) при P ₂ = 10P₁ , где P₁ и P₂ — одноименные энергетические величины

мощности, энергии, плотности энергии и т.д. В случае, если берется логарифмическая величина для отношения двух «силовых» величин (напряжения, силы тока, давления, напряженности поля и т.п.), бел определяется по формуле 1Б=2lg(F2/F1) при F₂ =√ ̅ 10F₁. Дольной единицей от бела является 0,1 Б.

1.4. Системы физических величин и единиц. Международная система единиц (система СИ)

По степени условной независимости от других величин данной группы ФВ делятся на основные (условно независимые), производные (условно зависимые) и дополнительные. Основные величины выбираются обосновано, но в общем произвольным образом. Производные величины выражаются через основные на основе известных уравнений связи между ними.

Совокупность основных и производных единиц ФВ, образованная в соответствии с принятыми принципами, называется системой единиц ФВ. Единица основной ФВ в данной системе является основной единицей системы.

Действующая в настоящее время «Международная система единиц» (сокращенное обозначение система СИ (SI) «система интернациональная») была принята Х1 Генеральной конференцией по мерам и весам в 1960 г. Система СИ — единственная система единиц ФВ, которая принята и используется в большинстве стран мира. Система Си состоит из 7 основных, 2 дополнительных и ряда производных единиц. Наименования основных и дополнительных единиц ФВ приведены в таблице 1.4.

На территории нашей страны система единиц СИ действует с 1 января 1982 г. в соответствии с ГОСТ 8.417-81 «ГСИ. Единицы физических величин». Она возникла не на пустом месте и является логическим развитием предшествовавших ей систем единиц: СГС (основные единицы: сантиметр — грамм — секунда), МКГСС (основные единицы: метр — килограмм-сила -секунда), МКС (основные единицы: метр — килограмм — секунда) и др.

Основные и дополнительные единицы ФВ системы СИ

№ п/п	Физическая величина	Единица измерения ФВ
Наименование	Размер ность	Рекоменд уемое обозначе ние	Наименован ие	Обозначение
русс кое	междун ародное
О с н о в н ы е
Длина	L	l	метр	м	m
Масса	M	m	килограмм	кг	kg
Время	T	t	секунда	с	s
Сила электрического тока	I	I	ампер	А	A
Термодинамическая температура	T	кельвин	К	K
Количество вещества	N	n, и	моль	моль	mol
Сила света	J	J	кандела	кд	cd
Д о п о л н и т е л ь н ы е
Плоский угол	—	—	радиан	рад	rad
Телесный угол	—	—	стерадиан	ср	sr

В названии системы ФВ применяют символы величин, принятых за основные. Например, система величин механики, в которой в качестве основных используются длина (L), масса (М) и время (Т), называется системой LMT. Действующая международная система единиц СИ должна обозначаться символами LMTI0 NJ, обозначающими соответственно символы основных величин: длины (L), массы (М) и времени (Т), силы электрического тока (I), температуры (0), количества вещества (N) и силы света (J).

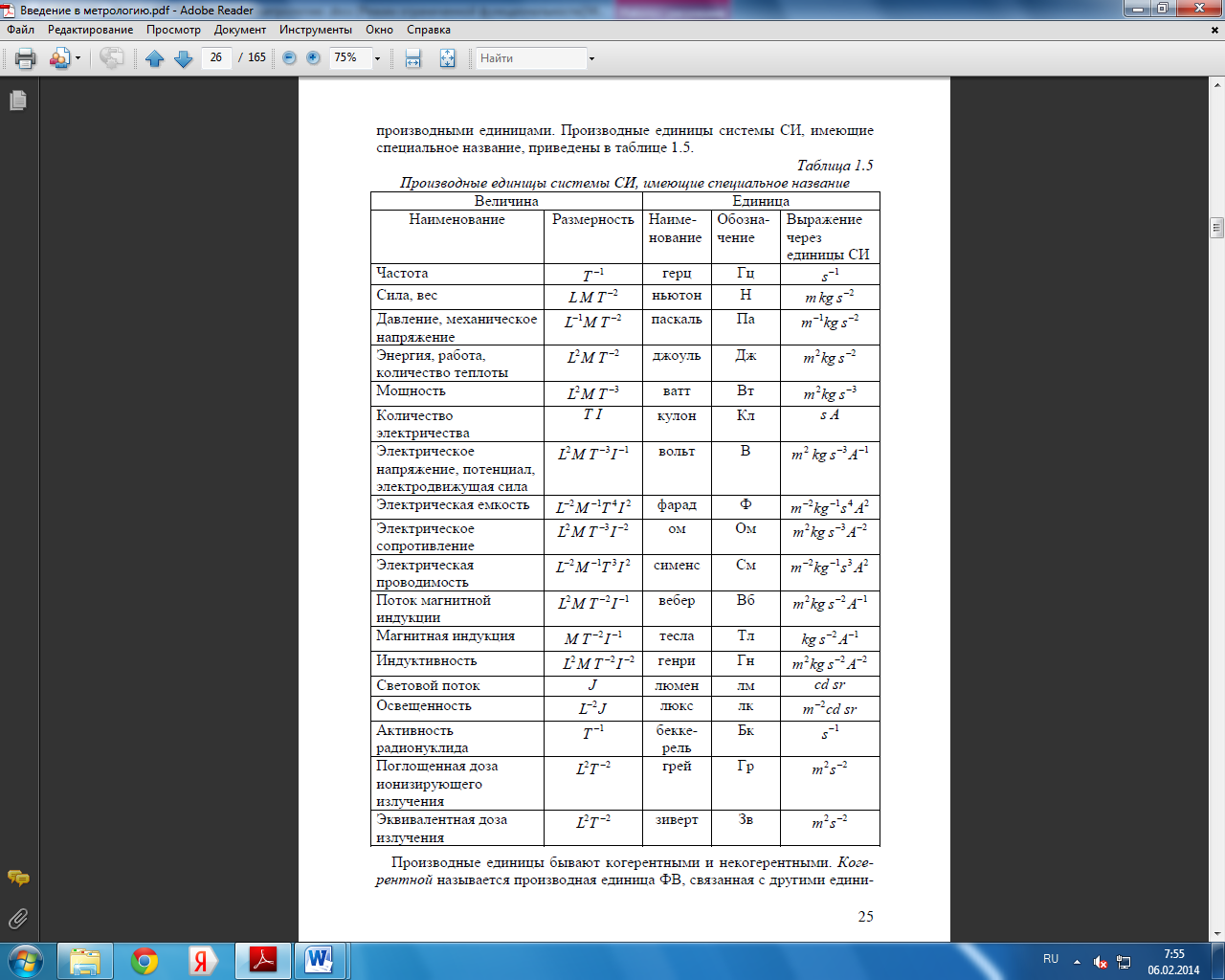
Производная единица системы единиц — это единица производной ФВ системы единиц, образованная в соответствии с уравнением, связывающим ее с основными единицами или же с основными и уже определенными производными единицами. Производные единицы системы СИ, имеющие специальное название, приведены в таблице 1.5.

Производные единицы системы СИ, имеющие специальное название

Производные единицы бывают когерентными и некогерентными. Когерентной называется производная единица ФВ, связанная с другими единицами системы уравнением, в котором числовой коэффициент принят равным 1.

Различают кратные и дольные единицы ФВ. Кратная единица — это единица ФВ, в целое число раз большая системной или внесистемной единицы. Дольная единица — единица ФВ, в целое число раз меньшая системной или внесистемной единицы. Приставки для образования кратных и дольных единиц СИ приведены в таблице 1.6.

Множители и приставки для образования десятичных

кратных и дольных единиц и их наименований

Множитель	Приставка	Обозначение приставки	Множитель	Приставка	Обозначение приставки
международное	рус ское	международное	русское
10 18	экса	Е	Э	10 -1	деци	d	д
10 15	пета	Р	П	10 -2	санти	с	с
10 12	тера	Т	Т	10 -3	милли	m	м
10 9	гига	G	Г	10 -6	микро	µ	мк
10 6	мега	М	М	10 -9	нано	n	н
10 3	кило	k	к	10 -12	пико	Р	п
10 2	гекто	h	г	10 -15	фемто	f	ф
10 1	дека	Da	да	10 -18	атто	а	а

Единицы ФВ делятся на системные и внесистемные. Системная единица — единица ФВ, входящая в одну из принятых систем. Все основные, производные, кратные и дольные единицы являются системными. Внесистемная единица — это единица ФВ, не входящая ни в одну из принятых систем единиц. Внесистемные единицы разделяют на четыре вида:

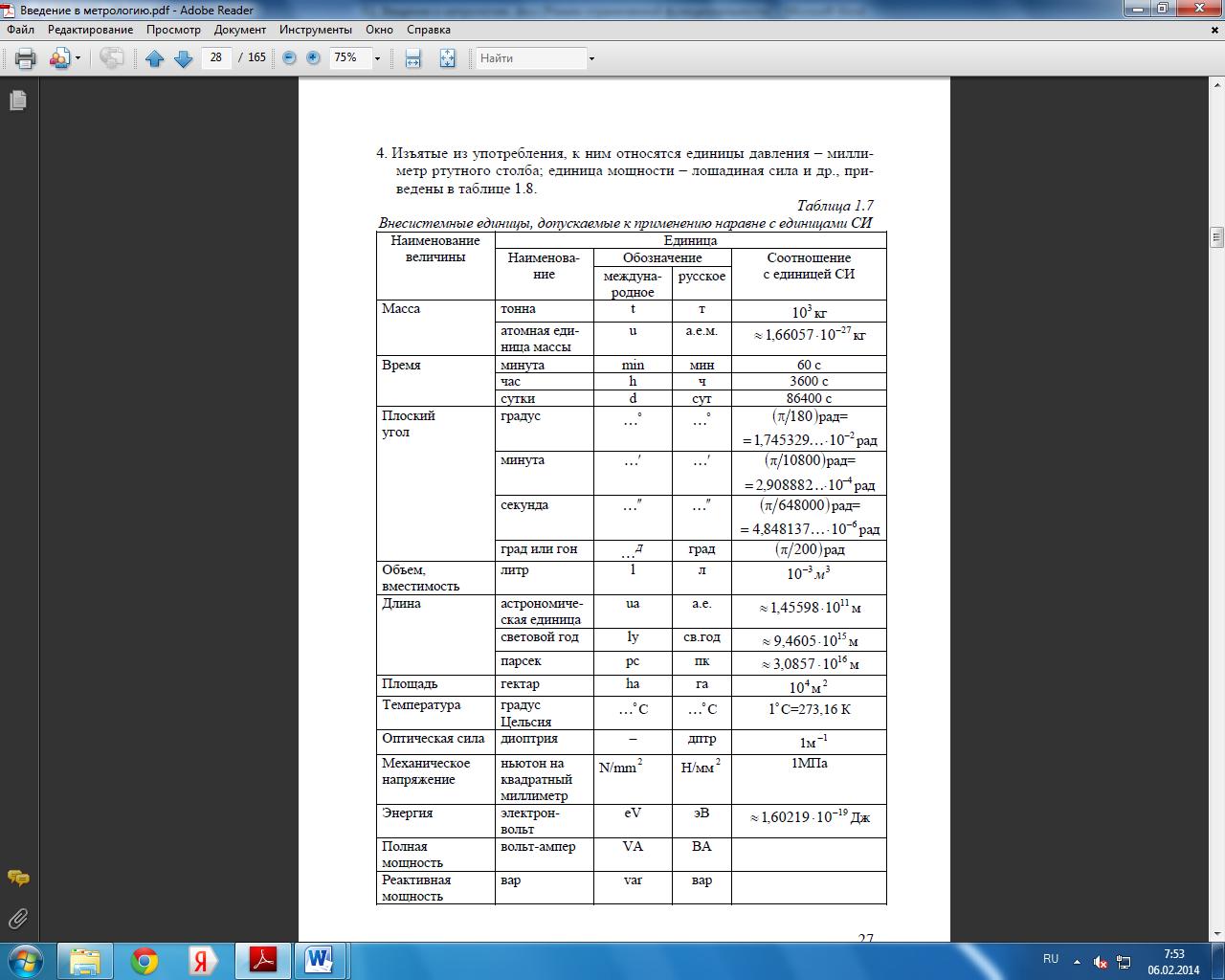
1. Допускаемые наравне с единицами СИ, например: единица массы -тонна; единицы плоского угла — градус, минута, секунда; единица объема — литр и др. Внесистемные единицы, допускаемые к применению наравне с единицами СИ, приведены в таблице 1.7.

2. Допускаемые к применению в специальных областях, к которым относятся: единицы длины (в астрономии) — астрономическая единица, парсек, световой год; единица оптической силы (в оптике) — диоптрия; единица энергии (в физике) — электрон-вольт, приведены в таблице 1.4.

3. Временно допускаемые к применению наравне с единицами СИ, например: в морской навигации — морская миля; в ювелирном деле единица массы — карат и др. Эти единицы должны изыматься из употребления в соответствии с международными соглашениями.

4. Изъятые из употребления, к ним относятся единицы давления — миллиметр ртутного столба; единица мощности — лошадиная сила и др., при­ведены в таблице 1.8

Внесистемные единицы, допускаемые к применению наравне с единицами СИ

Наименование величины	Единица
Наименование	Обозначе­ние	Соотношение с единицей СИ
Длина	микрон ангстрем	мк А	1 мк=10 -6 м 1 А=10 -10 м
Масса	центнер	цн	1 цн=10 кг
Площадь	ар	а	1 а=10 2 м 2
Сила	килограмм-сила тонна-сила дина	кгс тс дин	1 кгс=9,80665 Н 1 тс=9,80665 ■ 10 3 Н 1 дин=10 -5 Н
Работа и энергия	килограмм- сила-метр эрг ватт-час	кгсм эрг втч	1 кгсм=9,80665 Дж 1 эрг=10 -7 Дж 1 втч = 3,6 ■Ю 3 Дж
Мощность	лошадиная сила	л.с.	1л.с =735,499 Вт
Давление	бар Миллиметр ртутного столба Миллиметр водяного столба Техническая атмосфера Физическая атмосфера	бар мм рт. ст. мм вод. ст. ат атм	1 бар=10 5 Па 1 мм рт. ст.=133,322 Па 1 мм вод. ст.=9,80665 Па 1 ат=9,80665 ■ 10 4 Па 1атм=1,01325 ■ 10 5 Па (760 мм рт. ст.)
Угол поворота	оборот	об	1 об=2п рад
Угловая скорость	оборот в минуту оборот в секунду	об/мин об/с	1 об/мин=—рад/с 30 1 об/с=2п рад/с

Внесистемные единицы, изъятые из употребления, и их связь с единицами системы СИ

1.5. Контрольные вопросы

1. Определите основное понятие и предмет метрологии.

2. Укажите три раздела метрологии. По какому признаку проводится классификация разделов метрологии?

3. Что отличает метрологию от других естественных наук (физики, химии)?

4. Дайте определение физической величины. Приведите примеры физических величин, относящихся к механике, оптике, электричеству, магнетизму.

5. Что является качественной характеристикой физической величины?

6. Что является количественной характеристикой физической величины?

7. Используя основное уравнение измерения, объясните, почему значение физической величины не зависит от выбора единиц измерений?

8. В чем заключается суть измерения?

10. Является ли шкала наименований шкалой физических величин?

11. Объясните, почему на шкале порядка невозможно ввести единицу измерения.

12. Почему нельзя считать измерением определение значений величин с помощью шкал порядка?

13. Поясните, от каких величин зависит выбор начала отсчета на шкале интервалов. Приведите примеры шкал интервалов.

14. Можно ли определить размер физической величины с помощью шкал порядка?

15. Каким образом устанавливаются единицы измерений в шкалах отношений?

16. Поясните, почему абсолютные шкалы не зависят от принятой системы единиц измерения.

17. Дайте определение системы единиц ФВ.

18. Проведите классификацию ФВ по степени условной независимости от других величин данной группы ФВ.

19. Приведите примеры основных и производных ФВ.

20. Дайте определение кратных и дольных единиц. Приведите примеры.

Источник