Какие линии осей вращения при преобразовании чертежа способом вращения

Какие линии осей вращения при преобразовании чертежа способом вращения

Контрольные задания по теме: Рабочая тетрадь задача 50

Трудоемкость и точность графического решения задач часто зависит не только от сложности задач, но и от того, какое положение занимают геометрические фигуры по отношению к плоскостям проекций. Наиболее выгодными являются положения, параллельные плоскостям проекций или перпендикулярные им.

Переход от общего положения геометрической фигуры к частному можно осуществить двумя путями:

а) перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения;

б) выбором новой плоскости проекций, по отношению к которой фигура, не имеющая своего положения в пространстве, окажется в частном положении. Первый путь лежит в основе способа плоскопараллельного перемещения, а второй — в основе способа замены плоскостей проекций.

Существует несколько способов плоскопараллельного перемещения:

1. Способ параллельного перемещения. При этом плоскости, по которым двигаются точки фигуры, параллельны плоскости проекций. Траектория — произвольная плоская линия;

2. Способ вращения вокруг оси, перпендикулярной к плоскости проекций. Траектории перемещаемых точек — дуги окружностей, центры которых находятся на оси вращения;

3. Способ вращения вокруг оси параллельной плоскости проекций (вокруг линии уровня).

Это частный случай параллельного перемещения. За траекторию движения точки принимается не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между осью вращения и данной точкой.

При вращении точки вокруг оси перпендикулярной, П 2 , фронтальная проекция точки перемещается по окружности, а горизонтальная — по прямой, перпендикулярной оси вращения. Если же точка вращается вокруг оси, перпендикулярной П 1 , то в горизонтальной плоскости траекторией ее движения будет окружность, а во фронтальной – прямая, перпендикулярная оси вращения. На рисунке 32 показано построение новых проекций точек при помощи способа вращения. На рисунке 32 а – вращение вокруг фронтально-проецирующей оси, на рисунке 32 б – вокруг горизонтально-проецирующей оси.

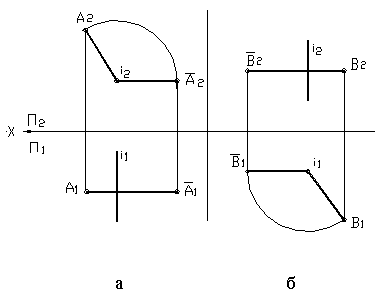
Рисунок 32

Этим способом удобно находить натуральные величины отрезков и фигур, занимающих проецирующее положение.

На рисунке 33 показан пример определения натуральной величины треугольника АВС, плоскость которого перпендикулярна П 2 . За ось вращения необходимо взять фронтально-проецирующую прямую, проходящую через точку, принадлежащую этой плоскости. В данном случае выбрана точка А — вершина треугольника. Плоскость треугольника вращается во фронтальной плоскости вокруг оси до положения, параллельного горизонтальной плоскости. Во фронтальной плоскости точки С и В перемещаются по окружностям, радиус которых равен расстоянию от оси вращения до фронтальных проекций точек. В горизонтальной плоскости траектории движения точек – прямые, перпендикулярные оси. Полученная проекция треугольника А´В´С´, является его натуральной величиной.

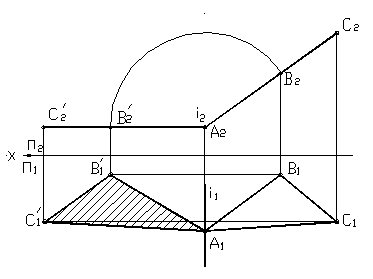
Рисунок 33

Способ вращения наиболее часто применяется при определении натуральных величин сечений поверхностей плоскостями частного положения.

Сущность этого способа состоит в том, что положение фигуры в пространстве не меняется, а вводится новая система плоскостей проекций. Новая плоскость проекции выбирается перпендикулярно к одной из старых. При этом, проецируемая фигура по отношению к новой плоскости занимает частное положение, обеспечивая наиболее удобное решение задачи. Если замена одной плоскости не обеспечивает требуемый результат, то новую плоскость заменяют еще раз.

На рисунке 34 показано построение проекции точки А в новой системе плоскостей проекций при замене плоскости П 1 на П 4 . Плоскость П 4 перпендикулярна П 2 . Проекция точки А1 заменяется на А 4 . По линии связи откладывается расстояние от заменяемой проекции точки до новой оси.

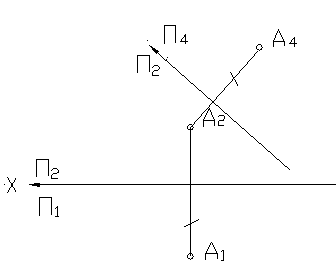
Рисунок 34

На рисунке 35 дан пример определения натуральной величины отрезка общего положения. Новая плоскость П 4 выбирается параллельно одной из проекций отрезка. При этом проекция отрезка на эту плоскость будет являться его натуральной величиной.

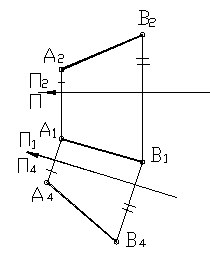
Рисунок 35

В некоторых случаях требуется замена двух плоскостей проекции. Например, при определении расстояния от точки до прямой. При этом прямую необходимо спроецировать в точку. На рисунке 36 отрезок общего положения переведен в проецирующее положение по отношению к плоскости П₅.

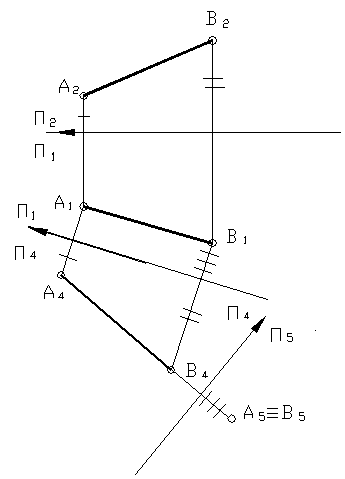
Рисунок 36

1. Назовите, какие вы знаете способы преобразования чертежа. Для чего они применяются?

2. Какие задачи можно решать при помощи способа вращения вокруг проецирующей оси?

3. По каким линиям перемещаются проекции точки при вращении вокруг горизонтально проецирующей оси?

4. Можно ли определить натуральную величину фигуры общего положения способом вращения вокруг проецирующей оси?

5. В чем суть способа замены плоскостей проекций?

6. Как построить проекцию точки в новой системе плоскостей проекций? Этапы построения.

7. Сколько замен нужно осуществить, чтобы перевести отрезок общего положения в проецирующее положение?

8. Как нужно выбрать новую плоскость, для того, чтобы сделать плоскость общего положения проецирующей?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Способы преобразования чертежа. Способ вращения.

Как известно, при вращении некоторой точки вокруг оси она движется в плоскости, перпендикулярной оси вращения, и описывает окружность. Для применения способа вращения в целях преобразования чертежа отметим следующие четыре эле­мента (рис. 5.8):

ось вращения (MN);

плоскость вращения точки (пл. S (MN));

В качестве оси вращения обычно используют прямые, пер­пендикулярные или параллельные плоскостям проекций. Рас­смотрим вращение относительно осей, перпендикулярных плоскостям проекций.

Вращение точки А на чертеже относительно оси MN,пер­пендикулярной плоскости Н, показано на рисунке 5.9. Плос­кость вращения S параллельна плоскости H и на фронтальной проекции изображена следом S_v.Горизонтальная проекция о центра вращения 0 совпадает с проекцией тп оси, а гори­зонтальная проекция oa радиуса вращения OA является его натуральной величиной. Поворот точки А на рисунке 5.9 про­изведен на угол φ против часовой стрелки так, чтобы в новом положении точки с проекциями а’₁, а₁ радиус вращения был параллелен плоскости V. При вращении точки вокруг верти­кальной оси ее горизонтальная проекция перемещается по ок­ружности, а фронтальная проекция – параллельно оси x перпендикулярно оси вращения.

Если точку вращать вокруг оси, перпендикулярной плоскости V, то ее фронтальная проекция будет перемещаться по окруж­ности, а горизонтальная – параллельно оси x.

Вращение точки вокруг проецирующей прямой применяют при решении некоторых задач, например при определении на­туральной величины отрезка прямой. Для этого (рис. 5.10) достаточно ось вращения с проекциями m’n’, тп выбрать так, чтобы она проходила через одну из крайних точек отрезка, на­пример точку с проекциями b’, b.Тогда при повороте точки А на угол φ в положение А₁ (ОА₁ ║ пл. V, оа₁ ║оси x)отрезок AB перемещается в положение А₁В,параллельное плоскости V и, следовательно, проецируется на нее в натуральную величину. Одновременно в натуральную величину будет проецироваться угол α наклона отрезка AB к плоскости H.

Рис. 5.10 Рис. 5.11

Поворот (вращение) точки с проекциями b’, b относитель­но оси с проекциями m’n’, mn, перпендикулярной плоскости V,показан на рисунке 5.11. При вращении точка В переме­щена в плоскости вращения T(T_h) в положение с проекциями b’₁, b₁ так, что радиус вращения OB стал параллелен плоско­сти H (o’b’ ║оси x).

Применение способа вращения без указания на чертеже осей вращения, перпендикулярных к плоскостям проекций.Если вращать геометрическую фигуру вокруг оси, перпендикуляр­ной к плоскости проекций, то проекция на этой плоскости не изменяется ни по виду, ни по величине (меняется лишь положение проекции относительно оси проекций). Проек­ции точек геометрической фигуры на плоскости, параллель­ной оси вращения, перемещаются по прямым, параллельным оси проекции (за исключением проекций точек, располо­женных на оси вращения), и проекция в целом изменяется по форме и величине. Поэтому можно применять способ вращения, не задаваясь изображением оси вращения. В этом случае, не изменяя величины и формы одной из проекций геометрического образа, перемещают эту проекцию в требу­емое положение, а затем строят другую проекцию так, как указано выше.

На рисунке 5.12 показано применение способа вращения без указания осей для определения натуральной величины треугольника ABC, заданного проекциями a’b’c’, abc. Для этого выполнено два поворота плоскости общего положения, в которой расположен треугольник так, чтобы после перво­го поворота эта плоскость стала перпендикулярной плоско­сти V, а после второго – параллельна плоскости H.Первый поворот вокруг оси, перпендикулярной плоскости H,без ука­зания ее положения осуществлен с помощью горизонтали с проекциями с’1′, с–1 в плоскости треугольника. При этом горизонтальная проекция abc повернута так, чтобы она сов­пала с направлением проецирования (с₁1₁ х).Горизонталь­ная проекция треугольника сохраняет свой вид и величину (a₁b₁c₁ = abc),изменяется лишь ее положение. Точки А, В и С при таком повороте перемещаются в плоскостях, парал­лельных плоскости H.Проекции а’₁ , с’₁ , b’₁ находятся на горизонтальных линиях связи а’ а’₁ , b’ b’₁ и с’ с’₁.Фронталь­ной проекцией треугольника в новом положении является отрезок а’₁ b’₁ с’₁ .

Второй поворот, приводящий треугольник в положение, параллельное плоскости H,производим вокруг оси вращения, перпендикулярной плоскости V (положение оси также не ука­зано). Фронтальная проекция при втором повороте сохраняет вид и величину, полученные после первого поворота. Точки A₁, B₁ и С₁ перемещаются в плоскостях, параллельных плоско­сти V.Проекции а₂, b₂, с₂ находятся на горизонтальных лини­ях связи а₁а₂ , b₁b₂ , c₁c₂.Проекция а₂b₂с₂ представляет собой натуральную величину данного треугольника.

При выполнении рассмотренных поворотов вокруг осей, перпендикулярных плоскостям проекций, эти оси не указаны, но их можно легко найти. Например, если провести отрезки aa₁, bb₁ и через их середины провести перпендикуляры, то полученная точка пересечения этих перпендикуляров и будет горизонтальной проекцией оси вращения, перпендикулярной к плоскости H.

Применение способа вращения без указания осей несколь­ко упрощает построения, не происходит наложения одной проекции на другую, но чертеж занимает большую площадь. (Рас­смотренный случай вращения без изображения осей вращения является частным случаем способа плоскопараллельного пере­мещения).

Источник

Метод вращения вокруг оси

Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.

Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

1. Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
2. При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
3. При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’₁ так, чтобы выполнялось условие C’₁D’₁ || X. Для нахождения точки C»₁ из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’₁.

На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁ CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂ отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁ проходит через точку D, а проекция i»₂ фронтально проецирующей прямой i₂ лежит на продолжении отрезка C»₁D»₁.

Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

1. Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
2. При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
3. При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f». Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

1. Проводим фронтальную проекцию h» горизонтали h. Она пересекает прямые a» и b» в точках 1» и 2». Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
2. Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
3. Определяем натуральную величину радиуса вращения R = O’A’₀. Для этого строим прямоугольный треугольник O’A’A’₀, катет которого A’A’₀ равен расстоянию от A» до h».
4. Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’₁. Соединяем A’₁ с точками 1′ и 2′. Искомый угол ϕ построен.

Источник