Какие используются способы задания положения опорных точек

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Способы задания положения точки и описание ее движения — Кинематика — МЕХАНИКА

1.1. Кинематика

1.1.5. Способы задания положения точки и описание ее движения

Положение точки в пространстве задается двумя способами:

1) с помощью координат; 2) с помощью радиус-вектора.

Положение точки с помощью координат задается тремя проекциями точки х, у, z на оси декартовой системы координат ОХ, ОУ, ОZ, связанные с телом отсчета (рис. 1.3). Для этого из точки А необходимо опустить перпендикуляры на плоскости УZ (координата х), ХZ (координата у), ХУ (координата z) соответственно. Записывается это так: А (х, у, z). Для конкретного случая, изображенного на рис. 1.3 (х = 6, у = 10, z = 4,5), точка А обозначается A (6; 10; 4,5).

Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения самой точки необходимо отложить значения координат на соответствующие оси (х на ось ОХ и т. д.) и на этих трех взаимно перпендикулярных отрезках построить параллелепипед. Вершина его, противоположная началу координат О и лежащая на диагонали параллелепипеда, и будет искомой точкой А.

Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчета точки достаточно провести две координатные оси: ОХ и ОУ. Тогда положение точки на плоскости определяют двумя координатами х и у (рис. 1.4).

Если точка движется вдоль прямой, достаточно задать одну координатную ось ОХ и направить ее вдоль линии движения.

Задание положения точки А с помощью радиус-вектора осуществляется соединением точки А с началом координат О (рис. 1.4). Направленный отрезок О А = называется радиус-вектором.

Радиус-вектор — это вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.

Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций rх, ry, rz на оси координат ОХ, ОУ, OZ, либо углы между радиус-вектором и осями координат. Для случая движения на плоскости (рис. 1.4) имеем:

Здесь r = | — модуль радиус-вектора , х и y — его проекции на оси координат, все три величины — скаляры; х и у — координаты точки А.

Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.

Вектор г можно также разложить на составляющие по осям X и У, т. е. представить в виде суммы двух векторов (рис. 1.4):

Таким образом, положение точки в пространстве задается либо ее координатами, либо радиус- вектором.

Способы описания движения точки

В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.

При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трех ее координат от времени:

Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т. е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.

При векторном способе описания движения точки изменение ее положения со временем задается зависимостью радиус-вектора от времени:

Уравнение (1.2) представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить ее положение (как и в случае координатного способа). Таким образом, задание трех скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).

Для каждого случая движения вид уравнений (1.1) или (1.2) будет вполне определенным. Если траекторией движения точки является прямая линия, движение называетсяпрямолинейным, а если кривая — криволинейным.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.

Источник

Кинематика. Задание положения точки.

Положение точки в пространстве можно задать двумя способами: координатным и векторным.

При задании движения координатным способом с телом отсчета связывают какую-либо систему координат, например, декартовую. Движение точки М будет задано в том случае, если ее координаты будут известны, как функции времени:

Эти зависимости называются уравнениями движения точки в декартовых координатах. Они выражают текущие координаты движущейся точки в виде функций времени. Если точка движется, оставаясь все время в одной плоскости, можно ограничиться двумя уравнениями движения: x = x(t), y = y(t).

Векторный способ задания положения точки .

Допустим, М – движущаяся точка относительно тела отсчета А. В теле А в качестве точки отсчета выберем произвольную точку О и построим вектор Этот вектор называется радиус-вектором точки М.

Радиус-вектор – это вектор, соединяющий начало отсчета с положением точки в любой момент времени.

Когда точка М движется, радиус-вектор непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени Зная эту функцию, для каждого времени t можно построить вектор и тем самым найти положение движущейся точки в данный момент. Функция называется векторным законом (векторным уравнением) движения точки М.

Точка задается радиус-вектором, если известны его длина (модуль) и направление в пространстве, другими словами – значения его проекций r_x, r_y, r_z на оси координат OX, OY и OZ, или углы между радиус-вектором и осями координат. При рассмотрении движения на плоскости:

Здесь за мы принимаем модуль радиус-вектора , а r_x и r_y являются его проекциями на оси координат, все три величины скалярны, x и y – координаты точки А.

Из этих уравнений видно, что между координатным и векторным способами задания положения точки существует связь.

Источник

Группа 831 21.03.2020

Уважаемые студенты. Выполнять задание необходимо в рабочей тетради и высылать фотоотчет о выполнении на почту преподавателя

Просмотр содержимого документа
«Группа 831 21.03.2020»

Для успешного освоения материала необходимо :

1 Ознакомиться с теоретическим материалом, составить краткий конспект и ответить на вопросы в конце лекции

Для тех, кто хочет более углубленно изучить данную тему в Приложении к лекции даны более углубленные сведения по данной теме!

Лекция: Понятие «эквидистанта к контуру». Методика построения эквидистанты

При обработке контура детали на станке с ЧПУ траектория движения инструмента представляет собой множество положений центра этого инструмента.

Различают следующие способы расположения траектории движения инструмента относительно контура детали:

Траектория совпадает с контуром детали (рис. 1, а).

Рис. 1.7. Варианты расположения траектории инструмента
относительно контура детали

Траектория эквидистантна (расположена по эквидистанте) контуру детали (рис. 1, б).

Эквидистанта — геометрическое место точек, равноудаленных от какой либо линии и лежащих по одну сторону от нее.

траектория изменяет положение относительно контура детали по определенному закону (рис. 1, в).

Для упрощения расчетов траекторию инструмента необхо­димо разбивать на отдельные участки, называемые геометриче­скими элементами траектории. К геометрическим элементам от­носятся отрезки прямых, дуги окружностей, кривые второго и высшего порядков.

Расчет траектории инструмента сводится к определению ко­ординат опорных точек, которые разделяют на геометрические и технологические.

Опорные геометрические точки — точки, в которых проис­ходит изменение закона, описывающего траекторию инструмен­та.

Опорные технологические точки — точки траектории, в которых происходит изменение условий протекания технологи­ческого процесса (изменение режимов обработки, временный ос­танов инструмента, включение или выключение охлаждения и т. д.).

Положение опорных точек может задаваться двумя спосо­бами:

в абсолютных размерах, когда координаты всех опорных точек заданы относительно одной точки (главным образом отно­сительно нуля детали).

в приращениях, когда координаты каждой последующей опорной точки заданы относительно предыдущей точки.

Выделяют графический и аналитический методы определе­ния координат опорных точек. При графическом методе коорди­наты опорных точек находят непосредственно с расчетно­технологической карты, построенной в требуемом масштабе. Данный метод характеризуется погрешностями построения тра­ектории и измерения размеров и часто не обеспечивает определе­ние координат с требуемой точностью. Более точным является аналитический метод, который заключается в расчете координат опорных точек через специальные уравнения и формулы.

При контурной обработке (траектория эквидистантна контуру) расчет координат опорных точек траектории включает два этапа:

Этап 1. Расчет координат опорных точек на контуре детали

В общем случае на данном этапе находят уравнения, описы­вающие геометрические элементы контура детали, и совместно решают эти уравнения для соседних геометрических элементов. Тем самым находят координаты опорных точек, расположенных на пересечении геометрических элементов контура детали. Ино­гда для расчета координат точек на контуре более удобным явля­ется использование специальных формул, получаемых через раз­меры геометрических элементов и координаты характерных то­чек этих элементов.

Наиболее часто решаются задачи определения координат опорных точек, лежащих на пересечении прямых и окружностей. Расчетные формулы для различных случаев пересечения прямых и окружностей представлены в табл. П.1.

Этап 2. Расчет координат опорных точек на эквидистанте

На данном этапе по специальным формулам производится расчет координат опорных точек на эквидистанте через коорди­наты соответствующих точек на контуре детали. Формулы для расчета координат опорных точек на эквидистанте для несколь­ких случаев представлены в табл. П.2.

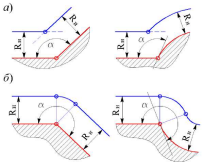
Используют два способа соединения элементов эквидистанты в зависимости от угла а между соседними геометрическими элементами контура детали:

при а 180° геометрические элементы эквидистанты со­единены дугой окружности радиусом , центр которой расположен в соответствующей опорной точке контура детали (рис. 2, б).

Рис. 2 Способы соединения элементов эквидистанты

Что такое исходная точка и руководствуясь чем выбирают ее положение при обработке на станках с ЧПУ?

Что представляет собой траектория движения инструмента (для положения какой точки задается и из каких элементов состоит)?

Что такое опорная точка траектории инструмента, и какие выделяют виды опорных точек?

Какие используются способы задания положения опор­ных точек?

Что такое эквидистанта, и каким образом координаты опорных точек на ней при использовании расчетно­аналитического метода?

эквидистанты, и в каких случаях?

Приложение к лекции.

Понятие «эквидистанта к контуру». Методика построения эквидистанты

Подготовка информации для управляющих программ Представление траектории обработки.

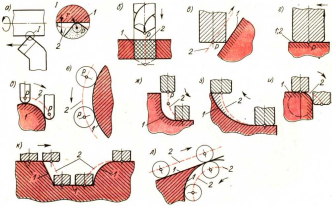
Детали, обрабатываемые на станках с ЧПУ, можно рассматривать как геометрические объекты. При обработке детали инструмент и заготовка перемещаются относительно друг друга по определенной траектории. Программа обработки детали задает (описывает) движение определенной точки инструмента — его центра (Р). Для концевой фрезы со сферическим торцом это центр полусферы, для концевой цилиндрической, сверла, зенкера, развертки — центр основания, для резцов — центр дуги окружности при вершине и т. д.

В процессе механической обработки деталей на станках с ЧПУ режущий инструмент (например, вершина резца или ось фрезы) должен перемещаться строго по определенной траектории относительно детали, причем точность перемещения и повторения этой траектории должна быть достаточно высокой, чтобы обеспечить точность размеров и контура всей партии обработанных деталей. В процессе ручного программирования технолог-программист на проекции чертежа детали изображает траекторию движения режущего инструмента, то есть наносит эквидистанту. Эквидистанта — линия, равноотстоя­щая от линии контура детали (заго­товки). При обработке на токарных станках с ЧПУ эквидистанта движения вершины резца совпадает с контуром обрабатываемой детали. Но эквидистанта, кроме точек обрабатываемого контура, содержит также и другие точки: исходную точку, точку начала обработки и др.

Исходная точка – это точка, из которой инструмент начинает свое движение и приближается к заготовке с целью ее последующей обработки. Точка начала обработки — это точка, оп­ределяющая начало обработки конкрет­ной заготовки. После обработки одной заготовки резец возвращается в исходную точку, из которой он начинает свое движение для обработки следующей заготовки. Таким образом, эквидистанта состоит из ряда точек, соединенных прямыми либо кривыми линиями в зависимости от того, какой контур детали следует обработать. Все точки эквидистанты называются ее базовыми или опорными точками.

Рис. 1. Схемы траекторий центра инструмента: 1 — контур детали; 2 — траектория

РЕКОМЕНДАЦИИ ПО ВЫБОРУ ОПОРНЫХ

Изобразив траекторию движения инструмента, необходимо нанести на эквидистанту опорные точки, при этом произвольно их наносить нельзя. Для выбора местоположения опорных точек следует соблюдать определенные рекомендации.

Исходную точку следует выбирать в зоне обработки так, чтобы инструмент, находящийся в этой точке, не вызывал затруднений при снятии обработанной детали и установке новой заготовки на станок. При обработке на токарных станках с ЧПУ исходную точку выбирают справа от заготовки на расстоянии, исключающем случайный контакт резца с заготовкой при ее установке на станок.

Координаты исходной точки могут быть рассчитаны по известной методике в зависимости от размеров заготовки и величины припусков на торцы и цилиндрические шейки детали. Исходная точка выбирается при токарной обработке каждой поверхности, то есть при обработке детали исходных точек несколько, каждая из них соответствует обработке конкретным инструментом.

Выбор места расположения исходной точки влияет на удобство установки и снятия детали (чем ближе расположена исходная точка к обрабатываемой детали, тем больше вероятность недопустимого контакта детали с резцом, чреватым сколом вершины резца). С другой стороны, чрезмерное удаление исходной точки эквидистанты от обрабатываемой заготовки приводит к увеличению пути холостого хода инструмента, а, следовательно, к увеличению вспомогательного времени на выполнение технологической операции, то есть снижению производительности обработки.

Из исходной точки режущий инструмент движется к заготовке на скорости холостого хода, которая является самой большой скоростью перемещения инструмента, допускаемой станком. Перемещение на скорости холостого хода программируется командой G00. Непосредственно перед заготовкой скорость режущего инструмента должна быть снижена до рабочей скорости подачи, для этого на расстоянии примерно 1,5 – 2,0 мм до контакта с заготовкой скорость движения инструмента переключается на рабочую. Мгновенное уменьшение скорости холостого хода до скорости рабочей подачи, ввиду инерционности технологической системы, произойти не может. Расстояние 1,5 – 2,0 мм необходимо для того, чтобы инструмент снизил свою скорость до рабочей, плавно вошел в контакт с заготовкой и начал процесс резания.

В связи с изложенным после исходной точки на эквидистанту следует нанести вторую точку, расположенную на расстоянии 1,5-2,0 мм от обрабатываемого контура детали. Третья, четвертая и т. д. точки эквидистанты совпадают с точками обрабатываемого контура детали, но чтобы не затемнять чертеж детали, участок эквидистанты, изображают параллельно контуру, а не по самому контуру. После окончания обработки контура резец следует отвести от детали и вернуть его на холостом ходу в исходную точку.

Каждый кадр УП содержит геометрические и технологические дан­ные, необходимые для обработки одного элементарного участка детали, чаще всего между двумя соседними опорными точками. Опорные точки обрабатываемого контура заготовки выбирают в местах, где инструмент изменяет свою скорость и направление движения (изменяет черновую на чистовую подачу), при переходе от обработки прямолинейного контура к криволинейному контуру и наоборот.

Опорные точки эквидистанты выбирает технолог – программист, который также рассчитывает их координаты (при ручном программировании). В дальнейшем координаты вписывают в кадры УП, которые содержат информацию о работе исполнительных органов станка: величины перемещения по координатам X, Z, скорость подачи, частоту вращения шпинделя, работу механизмов смены инструмента и др.

Источник