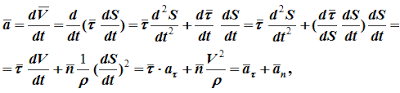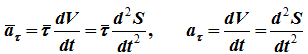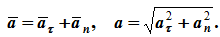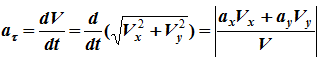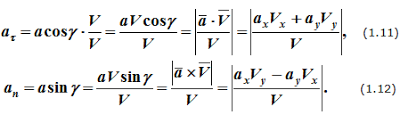Как задать движение точки естественным способом

Естественный способ задания движения точки

Введение

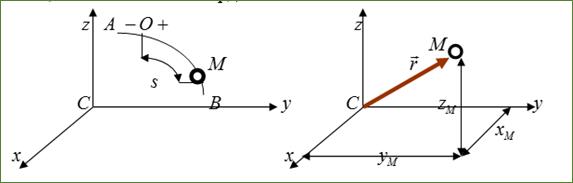
Естественный способ задания движения материальной точки применяется в тех случаях, когда траектория заранее известна. Например, точка движется внутри желоба в твердом теле. В этом случае мы, произвольным образом, выбираем некоторую неподвижную точку на траектории. Эту точку мы принимаем за начало отсчета. Далее мы произвольным образом выбираем положительное направление. Рассмотрим подвижную точку на траектории. Пусть – расстояние от точки до точки , измеренное вдоль дуги траектории. Введем криволинейную координату следующим образом. Если точка находится в положительном направлении относительно начала отсчета , то . Если точка находится в отрицательном направлении относительно начала отсчета , то . Тогда криволинейная координата однозначно определяет положение точки на траектории. При движении точки, координата изменяется со временем :
.

Таким образом, при естественном способе задания движения материальной точки, мы задаем следующие данные:
1) траекторию точки;
2) начало отсчета с указанием положительного и отрицательного направления отсчета;
3) криволинейную координату, как функцию от времени: .

Определение кинематических величин

В начале мы должны определить геометрические характеристики траектории – касательную, главную нормаль и радиус кривизны.

По заданной траектории, для любого положения точки, мы можем определить единичный вектор , направленный по касательной к траектории; единичный вектор , направленный вдоль главной нормали (к центру кривизны) траектории и радиус кривизны траектории. Поскольку вектор можно направить по касательной двумя взаимно противоположными способами, то мы направим вектор вдоль направления, которое мы приняли за положительное. Вектор можно направить только одним способом – к центру кривизны траектории. Векторы и представляют собой два орта естественного трехгранника. В простых случаях, найти векторы , и радиус кривизны траектории можно геометрическим способом (см. пример решения задачи ниже). Как найти эти величины в более сложных случаях, указано на странице “Оси естественного трехгранника”. Там же приводится пример определения векторов , и радиуса кривизны траектории для винтовой линии.

После того, как мы определили орты естественного трехгранника , и радиус кривизны траектории , мы можем найти векторы скорости и ускорения точки . Выводы представленных ниже формул даны на странице “Кинематика материальной точки”.

Дифференцируя по , находим проекцию скорости на вектор :
.
Модуль скорости:
.
Вектор скорости:
.
Скорость, как и следовало, направлена по касательной к траектории. Если скорость направлена в положительном направлении, то
.
Если скорость направлена в отрицательном направлении, то
.

Дифференцируя по , находим тангенциальное ускорение (проекцию ускорения на вектор ):
.
Вектор тангенциального ускорения:
.
Нормальное ускорение:
.
Вектор нормального ускорения:
.
Вектор полного ускорения:
.
Модуль полного ускорения:
.

Пример решения задачи

Точка движется по дуге окружности радиуса по закону

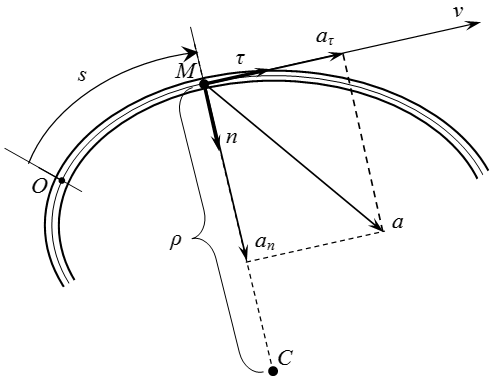
( s – в метрах, t – в секундах), где – расстояние от до , измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени . Изобразить на рисунке векторы и , считая, что точка в этот момент находится в положении , а положительное направление отсчета – от к .

Определим положение точки в момент времени .
.
Пусть – центр окружности. Угол между векторами и :
.
По условию, положительное направление – от к , то есть слева направо. Поскольку , то точка расположена слева от точки .

Дифференцируя по , находим проекцию скорости на направление касательной к траектории:
.
В момент времени :
.
Поскольку , то вектор скорости направлен по касательной к траектории в сторону возрастания . Абсолютное значение (модуль) скорости:
.

Дифференцируя по , находим касательное ускорение точки:

.
В момент времени :
.
Поскольку , то вектор касательного ускорения направлен по касательной к траектории в сторону возрастания .

Нормальное ускорение:
.
Вектор направлен к центру окружности.

Автор: Олег Одинцов . Опубликовано: 09-04-2016

Источник

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

При естественном способе задания движения точки предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.

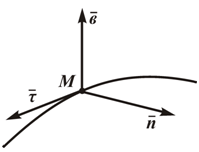
• τ — орт касательной;
• n — орт нормали;
• b — орт бинормали;

Единичные орты τ, n, b определяют направление соответствующих осей в каждой точке кривой.

Чтобы задать закон движения точки естественным способом необходимо:

1. знать траекторию движения;
2. установить начало отсчета на этой кривой;
3. установить положительное направление движения;
4. дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t).

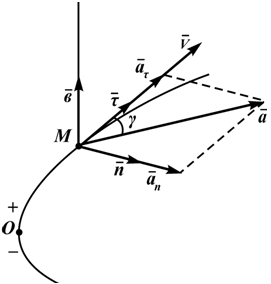
Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).

Скорость и ускорение точки

Скорость точки при естественном способе задания её движения определяется по формулам

Первая формула определяет величину и направление вектора скорости, вторая формула только величину.

Ускорение определяется как производная от вектора скорости:

оно характеризует быстроту изменения величины скорости точки;

Нормальное ускорение точки

характеризует быстроту изменения направления вектора скорости;

ρ — радиус кривизны траектории в данной точке (например, для окружности: ρ = R, для прямой линии ρ = ∞).

Полное ускорение точки при естественном способе задания движения определяется следующим образом (рисунок 1.5):

Ранее отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому, например, от координатного к векторному. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.

Далее, для естественнго способа задания движения точки, получаем

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Естественный способ задания движения точки

КИНЕМАТИКА ТОЧКИ

Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения материальных тел без учета их инертности (массы), а также причин, вызывающих данное движение (сил).

Кинематика представляет собой, с одной стороны, введение в динамику, так как здесь вводятся основные понятия и зависимости, необходимые для изучения движения тел с учетом действия сил. С другой стороны, методы кинематики имеют и самостоятельное практическое значение, например, при изучении движения в механизмах.

Под движением в механике понимается изменение с течением времени положения данного тела в пространстве по отношению к другим телам. Для определения положения движущегося тела с тем телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему осей координат, которую будем называть системой отсчета.

Если координаты всех точек тела в выбранной системе отсчета остаются все время постоянными, то тело по отношению к данной системе отсчета находится в покое. Если координаты каких-нибудь точек тела с течением времени изменяются, то тело по отношению к данной системе отсчета находится в движении.

Движение тел совершается в пространстве с течением времени. Пространство в механике рассматривается как трехмерное, а время считается универсальным, т.е. протекающим одинаково во всех системах отсчета. Время является скалярной, непрерывно меняющейся величиной. В задачах кинематики оно принимается за независимую переменную (аргумент), а все остальные величины (координаты, скорости и т.д.) рассматриваются как функции этого аргумента.

Кинематику делят на кинематику точки и кинематику системы материальных точек (тела). В кинематике решаются две основные задачи:

• первая состоит в установлении математических способов задания движения точек или тел;
• вторая заключается в том, чтобы, зная закон движения данного тела или точки, определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой из его точек в отдельности.

Для решения задач кинематики необходимо, чтобы непосредственно был задан или закон движения данного тела, или закон движения какого-нибудь другого тела, кинематически связанного с данным.

Способы задания движения точки

Чтобы задать движение точки, надо задать ее положение по отношению к выбранной системе отсчета в любой момент времени. Для этого задания можно применять один из трех способов: естественный, координатный, векторный.

Естественный способ задания движения точки

Естественным способом задания движения пользуются в тех случаях, когда траектория движущейся точки известна заранее. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория является прямой линией, то движение точки называется прямолинейным, а если кривой линией – то криволинейным.

Пусть точка движется относительно системы отсчета вдоль некоторой траектории . Выберем на этой траектории какую-нибудь неподвижную точку , которую примем за начало отсчета, а затем, рассматривая траекторию как координатную ось, установим на ней положительное и отрицательное направление, как на обычной координатной оси.

Тогда положение точки на траектории будет однозначно определяться криволинейной координатойs, равной расстоянию от точки до точки , измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка будет перемещаться вдоль траектории, следовательно, расстояние s будет с течением времени изменяться. Чтобы определить положение точки на траектории в любой момент времени, надо знать зависимость вида

s=f(t)

Это уравнение выражает закон движения точки. Таким образом, чтобы задать движение точки естественным способом, необходимо знать:

· траекторию движения точки;

· начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета;

· закон движения точки вдоль траектории: s=f(t)

Следует отметить, что величина s определяет положение точки, а не пройденный ею путь. Например, если точка, двигаясь из начала отсчета , доходит до положения , а затем, двигаясь в обратном направлении, приходит в положение , то в этот момент ее координата , а пройденный за это время путь будет равен .

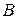
Источник