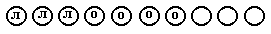Как задача решается двумя способами

Решение задач разными способами – средство повышения интереса к математике.
методическая разработка по математике (1 класс) по теме

Среди всех мотивов учебной деятельности самым действенным является познавательный интерес, возникающий в процессе обучения. Он не только активизирует умственную деятельность в данный момент, но и направляет ее к последующему решению различных задач.

Устойчивый познавательный интерес формируется разными средствами. Одним из них является решение задач разными способами.

Скачать:

Вложение	Размер
Решение задач разными способами	28.24 КБ

Предварительный просмотр:

Войнова Светлана Юрьевна, учитель начальных классов,

МОУ «СОШ №56 с углубленным изучением отдельных предметов»

Решение задач разными способами – средство повышения интереса к математике.

Люди научились считать 25-30 тысяч лет тому назад. О значении математики как предмета школьного преподавания М.В.Ломоносов в записке о преподавании физики, химии и математики пишет так:

«А математику уже затем учить следует, что она ум в порядок приводит».

Среди всех мотивов учебной деятельности самым действенным является познавательный интерес, возникающий в процессе обучения. Он не только активизирует умственную деятельность в данный момент, но и направляет ее к последующему решению различных задач.

Устойчивый познавательный интерес формируется разными средствами. Одним из них является решение задач разными способами.

Большие возможности для развития интереса учащихся к математике имеют задачи и их решения разными способами. Для кого из ребят интересна математика? Да математику любят в основном те ученики, которые умеют решать задачи, научив их решать задачи разными способами, мы окажем существенное влияние на их интерес к предмету, на развитие мышления и речи.

Однако в практике обучения математике различные способы решения ещё не заняли достойного места. Причин этому много, и в частности, недостаточная ориентация на эту работу в учебниках, методических пособиях для учителей. Учитель поэтому зачастую не владеет теми приёмами, с помощью которых можно отыскать другие способы решения. А без этого невозможно и детей научить находить разные способы решения, трудно использовать эти способы решения для других целей обучения и воспитания.

В начальном курсе математики текстовые задачи могут быть решены различными способами : алгебраическим, практическим, графическим, табличным, схематическим, комбинированным.

Рассмотрим различные способы решения текстовых задач на конкретных примерах.

Начальный курс математики ставит своей основной целью научить младших школьников решать задачи арифметическим способом, который сводится к выбору арифметических действий, моделирующих связи между данными и искомыми величинами. Решение задач оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением.

Задача. «Утром ушли в море 20 маленьких и 8 больших рыбачьих лодок, 6 лодок вернулись. Сколько лодок с рыбаками должно вернуться?»

I способ. 1. 20+8=28(л.) ушли в море.

2. 28-6=14(л.) должны вернуться.

II способ. 1. Сколько больших лодок должно вернуться? 20-6=14(л.)

2. Сколько всего лодок должно вернуться? 14+8=22(л.)

III способ. 1. Сколько маленьких лодок должно вернуться? 8-6=2(л.)

2.Сколько всего лодок должно вернуться? 20+2=22(л.)

Ответ: должно ещё вернуться 22 лодки. Задача решена различными арифметическими способами.

Если у учащихся нет навыков решения задач различными арифметическими способами или вызывает затруднение их нахождение, можно предложить следующие методические приёмы:

1. разъяснение плана решения задачи;

2. пояснение готовых способов решения;

3. соотнесение пояснения с решением;

4. продолжение начатых вариантов решения;

5. нахождение «ложного» варианта решения из числа предложенных.

Текстовые задачи решаются либо синтетическим методом (вычисления в прямом порядке, от числовых данных условия к числовым результатам, о которых спрашивается в задаче), либо аналитическим (вычисления в обратном порядке с рассуждениями, идущими от вопроса задачи). Примерами этих последних являются задачи о «задуманном числе», а также задачи на части. Естественным оформлением решения таких задач служит составление уравнения – алгебраический метод. Он состоит из следующих шагов: 1.Введение неизвестного. 2.Выражение через это неизвестное величин, о которых говорится в задаче. 3.Составление уравнения. 4.Решение уравнения. 5.Осмысление результата и формулирование ответа.

Задача: «У Иры втрое больше наклеек, чем у Кати, а у Кати на 20 наклеек меньше, чем у Иры. Сколько наклеек у Кати?».

Вначале составим схему уравнения, содержащую не только математические знаки, но и естественные слова.

( Ирины наклейки) – (Катины наклейки) = 20 наклеек.

Получилась вспомогательная модель задачи – частичный перевод текста на математический язык. Введём неизвестное. Пусть х – число Катиных наклеек. Тогда число наклеек у Иры равно х 3.

Составим уравнение х * 3 – х = 20

Ответ: у Кати 10 наклеек.

При обучении алгебраическому методу решения текстовых задач полезно дополнить схему решения самым первым шагом – составлением схемы уравнения, в которую включаются как математические символы, так и нематематические записи и даже рисунки.

Это способ решения задачи с помощью чертежа.

Задача: «Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?»

лещи окуни щуки

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

Построение чертежа помогает найти другой арифметический способ решения задачи.

Задача: «На одной машине увезли 28 мешков зерна, на другой на 6 мешков больше, чем на первой, а на третьей на 4 мешка меньше, чем на второй. Сколько мешков зерна увезли на третьей машине?»

I способ. 1. 28+6=34 (мешка) – увезли на второй машине.

2. 34-4=30 (мешка)- увезли на третьей машине.

Ответ : на третьей машине увезли 30 мешков зерна.

Если же мы построим чертеж к этой задачи, то легко найдем другой арифметический способ решения.

1. На сколько больше мешков увезли на третьей машине, чем на первой? 6-4=2(мешка)
2. Сколько мешков увезли на третьей машине? 28+2=30 (мешков)

Ответ: на третьей машине увезли 30 мешков зерна.

Из приведенных примеров следует вывод: графическое оформление задачи может определить ход мыслительного процесса и является средством выявления различных способов решения одних и тех же задач. При этом легче усматриваются разные логические основы, содержащиеся в условии задачи; такие способы определяются анализом наглядного сопровождения задачи, на которые учащиеся направляются постановкой учителем соответствующих заданий.

Задача: «В 6 банок поровну разложили 12 кг варенья. Сколько надо таких же банок, чтобы разложить 24 кг варенья?»

В данном случае логическая основа задачи проявляется на двух уровнях – открытом и скрытом, т. е. здесь две логические основы. В первом случае направление мыслительного процесса определяется вопросами:

1. Сколько кг варенья помещается в одну банку? 12:6=2(кг)
2. Сколько банок потребуется для 24 кг варенья? 24:2=12(б.)

Во втором случае ход того же процесса определяется другими вопросами:

1.Во сколько раз больше стало варенья? 24:12=2(раза)

Если варенья стало в два раза больше, значит, и банок потребуется в два раза больше.

2.Сколько потребуется банок? 6 * 2=12(б.)

Ответ: потребуется 12 банок.

При решении некоторых задач хорошим подспорьем является табличная форма.

Задача: «У Саши в коллекции 8 жуков и пауков. У всех насекомых 54 ноги. У одного жука 6 ног, а у одного паука – 8ног. Сколько жуков и сколько пауков у Саши в коллекции?»

Источник

Как задача решается двумя способами

СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.

С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.

Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?

Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.

Для решения можно применить алгебраический способ, рассуждая при этом так: “Число тарелок неизвестно, обозначим их буквой Х. На каждой тарелке 2 яблока, значит число всех яблок — это 2х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2х = 8 и решить его х = 8 : 2, х = 4”.

Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.

Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?

Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим

пойманных рыб: л — лещи, о — окуни.

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).

1) 3 + 4 = 7 (р.) — пойманные рыбы

Для ответа на вопрос задачи мы выполнили два действия.

Пусть х — пойманные щуки

Тогда количество всех рыб можно записать выражением:

3 + 4 + х — все рыбы

По условию задачи известно, что рыбак поймал всего 10 рыб.

Значит 3 + 4 + х = 10

Решив это уравнение, мы ответим на вопрос задачи.

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.

У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?

а) решение по действиям

Ответ: 50 книг на третьей полке.

б) по действиям с пояснением

1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.

2) 90 — 10 = 50 (к.) на 3 полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

90 — (28 + 12) = 50 (к.)

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90 — 28 = 62 (к.) на 2 и3 полках.

2) 62 — 12 = 50 (к.) на 3 полке.

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

1) 90 — 12 = 78 (к.) на 2 и 3 полках.

2) 78 -28 = 50 (к.) на З полке.

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Конспект урока «Решения задачи 2 способами»

Решение задачи двумя способами.

Тип урока: урок открытия новых знаний

Цель: создать условия для развития умений решать задачи разными способами; формировать умение использовать различные формы записи условия задач.

Предметные: научатся решать задачи разными способами; сформировать умение использовать различные формы записи условия задач.

Познавательные: научатся находить способ решения учебной задачи и выполнять учебные действия в устной и письменной форме.

Регулятивные : принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями её реализации.

Коммуникативные: научатся сотрудничать со сверстниками и учителем через ИКТ.

Личностные: проявляют положительное отношение к школе и учебной деятельности; имеют представление о причинах успеха в учёбе; выражают этические чувства на основе анализа простых ситуаций.

I . Организационный момент.

-Здравствуйте, ребята. Откройте пожалуйста тетради и запишите:

II. Актуализация знаний.

1) 6 увеличить в 4 раза, полученное число уменьшить в 2 раза, полученное число увеличить на 18, полученное число уменьшить на 30.

2) 27 уменьшить в 3 раза, полученное число увеличить в 4 раза, полученное число увеличить на 4; сколько не хватает до 100?

3) 72 уменьшить в 9 раз, полученное число увеличить в 8 раз, увеличить на 36.

III. Постановка цели и задач урока.

‒ Сегодня мы будем учиться одну и ту же задачу решать разными способами.

Чтение, разбор условия и записи решений задачи № 847 по вопросам учителя:

‒ Как рассуждала Вера? Задайте вопросы к первому, ко второму и третьему действиям её решения.

В первом действии Вера узнала, сколько стоит 6 кустиков огуречной рассады.

Во втором действии Вера узнала, сколько стоит 2 кустика огуречной рассады.

Вера узнала сколько стоила вся рассада.

‒ Как рассуждал Дима? Задайте вопросы к первому и второму действиям его решения.

В первом действии Дима узнал сколько всего кустиков рассады купила мама.

Во втором действии Дима узнал сколько стоила вся рассада.

Сравнение обоих решений и выяснение, какой способ лучше.

-Какое решение лучше и быстрее?

IV .Первичное усвоение новых знаний

Решение задачи № 848 (1)

— Сколько цветочков из бисера делает Кристина за один урок? (6) А Даша?

Прочитаем условие задачи.

-Сколько цветочков сделают обе девочки за 6 уроков?

-Краткое условие задачи можно записать в виде текста, рисунка, таблицы.

Сегодня мы запишем краткую запись условия задачи в виде таблицы.

-Вопрос мы писать не будем, т.к. знак вопроса мы поставили в таблице.

— При разборе задачи № 847, мы увидели, что некоторые задачи можно решить несколькими способами! Давайте решим эту задачу в три действия.

-Что спрашивается в задаче? Что нам нужно знать, чтоб ответить на вопрос задачи? (Сколько цветочков делает Кристина за 6 уроков и сколько цветочков делает Даша за 6 уроков)

-Из тех данных, которые нам нужны, что нам известно и что нужно узнать?

(Нам известно, что Кристина за 1 урок делает 3 цветочка, а Даша 4. Но не известно сколько цветочков делала Кристина за 6 уроков и неизвестно сколько Даша делала цветочков за 6 уроков).

-Можно ли это узнать? Что нужно для этого сделать, чтобы узнать сколько цветочков за 6 дней сделала Кристина?

-Что нужно сделать, чтобы узнать сколько цветочков за 6 дней сделала Даша?

-Теперь мы можем ответить на вопрос задачи? Что нужно для этого сделать?

Решение задачи в 2 действии.

-Скажите, что мы можем узнать в первом действии? (Сколько цветочков сделали девочки за один урок)

— Что нужно сделать, чтобы ответить на этот вопрос? Нужно к 3 цветочкам прибавить 4 цветочка, получится 7 цветочков.

-Сколько уроков нужно было делать цветочки Кристине и Даше? 6 уроков

-А за один урок вместе, сколько они сделают цветочков? 7 цветочков.

-А как нам узнать, сколько они вместе сделают цветочков за 6 дней? Нужно по 7 цветочков взять 6 раз, получится 42 цветочка.

V .Первичная проверка понимания

Самостоятельное решение задачи № 848 (2) двумя способами.

— Дети, что вам на уроке понравилось?

-Какие задания вы бы хотели повторить на следующем уроке?

-Скажите, пожалуйста, что у вас вызвало затруднения?

-Спасибо за урок. Будьте здоровы. До свидания!

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 809 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 285 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 601 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1259959

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Спортивные и творческие кружки должны появиться в каждой школе до 2024 года

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Российский совет олимпиад школьников намерен усилить требования к олимпиадам

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Читайте также:  Международные способы защиты трудовых прав