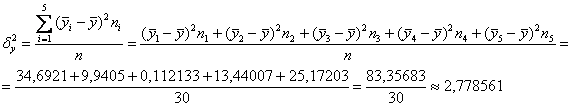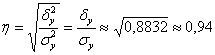Как выполнить способ группировки

Способ группировки

Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.

Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.

1. Подчеркнуть повторяющиеся буквы и записать друг за другом одночлены с одинаковыми буквенными множителями.
2. Вынести общий множитель за скобки у каждой группы одночленов.
3. Вынести полученный общий многочлен за скобки.

Рассмотрим пример разложения многочлена на множители способом группировки.

Подчеркнем повторяющиеся буквенные множители в одночленах.

Примеры способа группировки

Группировать одночлены можно по-разному. При правильной группировке должен появиться общий многочлен .

Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.

Первый способ

Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.

48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )

Второй способ

Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.

48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)

В итоге получился такой же ответ, как и при первом способе.

Рассмотрим еще один пример разложения многочлена способом группировки.

4q(p − 1) + p − 1 = 4q(p − 1) + (p − 1) = 4q(p − 1) + 1 · (p − 1) = (p − 1)(4q + 1)
В этом примере следует отметить, что для вынесения общего многочлена мы добавили умножение на 1 к многочлену (p − 1) , что не изменяет результат умножения.
Это помогает понять, что останется во второй скобке после вынесения общего многочлена.

Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.

Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.

2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)

Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.

• 2m(m − n) + n − m = − 2m( − m + n) + (n − m) = −2m(n − m) + 1 · (n − m) =
  = (n − m)(−2m + 1)

Источник

16. Аналитическая группировка

До сих пор нам встречалась одна статическая совокупность, с которой можно сделать много хороших и полезных вещей, но, как вы понимаете, там, где одна, там и две, и три и больше совокупностей. Причём, одна совокупность может зависеть от другой. О подобных связях и пойдёт речь далее по курсу. Добро пожаловать в новую, ещё более яркую и интересную реальность!

И начнём мы с аналитической группировки – популярной и несложной задачи, которая встречается повсеместно, особенно её любят предлагать студентам-экономистам. На данном уроке вы узнаете, что такое аналитическая группировка и научитесь БЫСТРО выполнять это действие. Объяснять, как обычно, буду на конкретном примере:

…да, это уже задача предпенсионного возраста 🙂

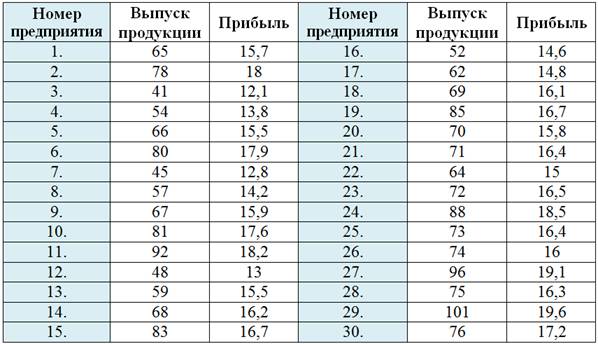
Имеются выборочные данные о выпуске продукции и сумме прибыли (млн. руб.) по 30 предприятиям:

Задание для начинающих:

1) Методом аналитической группировки установите наличие и характер корреляционной связи между стоимостью произведенной продукции и суммой прибыли на одно предприятие (результаты оформите в виде групповой и аналитической таблицы).

И пункт для продолжающих, продолжить рекомендую всем;)

2) Измерьте тесноту корреляционной связи между стоимостью произведенной продукции и суммой прибыли эмпирическим корреляционным отношением

Сделайте выводы. И мы их сделаем! Разберёмся в задании, решим и сделаем:

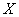
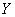
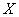
Итак, по условию нам даны две статистические совокупности: – выпуск продукции по предприятиям (в млн. руб.) и – прибыль по соответствующим предприятиям (тоже в млн. руб.). Зададимся вопросом: как влияет стоимость произведённой продукции (выпуск) на размер прибыли? Очевидно, что чем больше предприятие выпускает, тем больше у него прибыль. Но всегда ли это так? Нет не всегда. Ведь крупное предприятие может быть и убыточным, может не продать всю продукцию при увеличении её производства. Однако общая тенденция состоит в том, что при увеличении выпуска продукции, увеличивается и средняя прибыль по предприятиям. Ибо масштаб имеет значение, пекарни – это пекарни, а хлебзаводы – это заводы. НО при увеличении значений , тем не менее, нам могут встретиться и отдельные дышащие на ладан предприятия и даже гиганты в предбанкротном состоянии.

Такая нежёсткая зависимость называется корреляционной, о ней я уже немного рассказывал в курсе теорвера на уроке Зависимость и коэффициент ковариации непрерывных случайных величин. Но этот страх мало кто читал, поэтому я объяснил всё заново 🙂 И повторю ещё не раз.

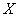
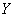
Совокупность (выпуск продукции) называется факторной (причинной) или признаком-фактором. Совокупность (прибыль) называется результативной (следственной) или признаком-результатом.

Но не всё так просто. Дело в том, что вышесказанное является лишь нашим предположением. А вдруг в условии дано 30 каких-нибудь северокорейских заводов, где нет такой зависимости?

Именно поэтому по условию задачи требуется установить наличие и характер корреляционной связи между стоимостью произведенной продукции и суммой прибыли на одно предприятие. Под характером связи понимается её направление, при этом возможны следующие варианты:

– прямая связь («чем больше, тем больше» – наш случай);
– обратная связь («чем больше, тем меньше»);
– отсутствие связи («чем больше, тем так же хаотично»).

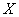
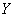
И установить всё это нужно методом аналитической группировки – данная группировка позволяет выяснить наличие и направление корреляционной связи между признаком-фактором и признаком-результатом .

И мы начинаем, наконец, оформлять решение:

Прежде всего, нужно определить признак-фактор и признак-результат. Самостоятельно, на основе логических рассуждений. Тут же высказываем предположение о наличии и направлении предполагаемой корреляционной связи. В нашей задаче можно записать примерно следующее:

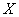
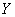
Очевидно, что средний размер прибыли по предприятиям зависит от стоимости выпущенной продукции, при этом, чем больше выпущено продукции, тем выше может быть прибыль. Таким образом, выпуск продукции является признаком-фактором, а прибыль предприятий – признаком-результатом; предполагаемая корреляционная зависимость – прямая.

Обращаю ваше внимание, что эта часть задания является если не обязательной, то строго желательной. Часто в условии прямо запрашивается этот пункт.

Теперь проверяем нашу гипотезу (предположение) методом аналитической группировки.

Как выполнить аналитическую группировку?

Сначала нужно упорядочить совокупности по признаку-фактору. Расположим предприятия по возрастанию выпуска продукции (оранжевый цвет):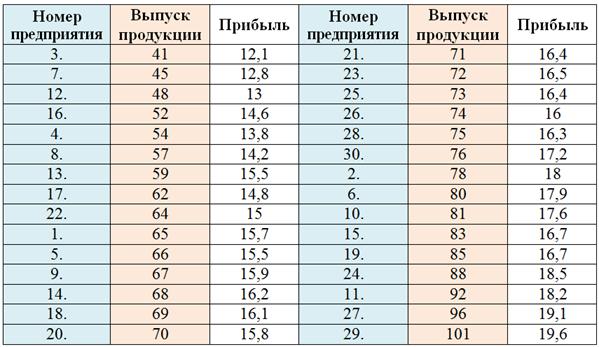

В Экселе эта сортировка выполняется буквально в пару щелчков, и чуть ниже будет ролик о том, как быстро решить нашу задачу. Номера предприятий можно было опустить, но я оставил их для лучшего понимания выполненного действия.

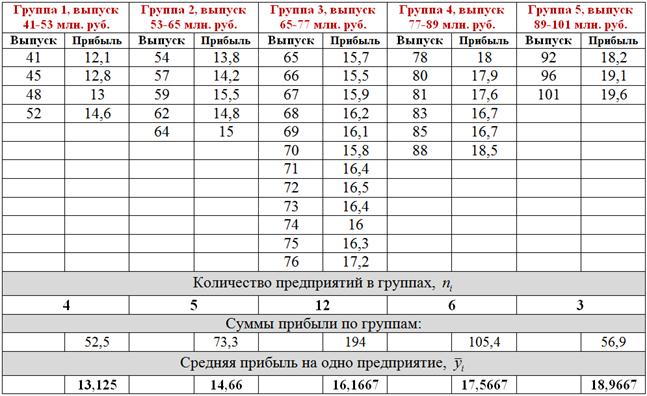
Теперь выполняем группировку совокупностей – опять же по признаку-фактору (выпуску продукции). Поскольку в условии нет никаких указаний на этот счёт, то используем стандартную равноинтервальную группировку. Размах вариации составляет:
млн. руб., оптимальное количество интервалов определим по формуле Стерджеса, для объёма совокупности оно составляет:

интервалов

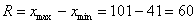
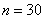
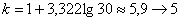
Таким образом, длина каждого интервала: 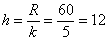млн. руб., в результате чего у нас получаются интервалы: 41-53, 53-65, 65-77, 77-89 и 89-101 млн. руб. Собственно, организуем группы и начинаем заполнять групповую таблицу. Напоминаю, что значения, попадающие на «стык» интервалов следует относить в следующий интервал:

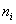
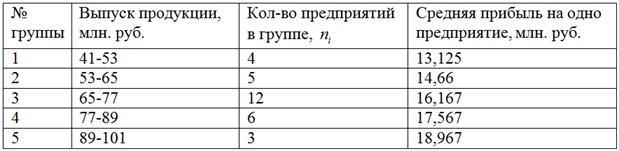
В нижней части таблицы подсчитываем количество предприятий по каждой группе, сумму значений (внимание!) результативного признака (прибыли), и, наконец, средние значения результативного признака по группам.

Основные результаты представим в виде аналитической таблицы:

Теперь смотрим короткое видео о том, как это всё быстро подсчитать:

Как выполнить аналитическую группировку в MS Excel? (Ютуб)

Сделаем краткие выводы: аналитическая группировка показала, что при увеличении стоимости выпущенной продукции наблюдается увеличение средней прибыли по предприятиям. Таким образом, между рассмотренными факторами действительно существует прямая корреляционная зависимость.

То есть, наше предположение (см. начало задания) подтвердилось.

Обращаю внимание, что средние значения (правая колонка) не обязаны строго возрастать (либо убывать), и если вы получите такой результат, то это будет нормально, ведь корреляционная зависимость не является жёсткой. ВажнА общая тенденция увеличения (либо уменьшения) средних значений. Но может статься, что по итогу вообще не проучится какой-то внятной закономерности. И это тоже результат исследования! С соответствующими выводами о слабой зависимости либо отсутствии таковой.

И вот здесь мы как раз подошли ко второму пункту задания: представьте, что значения признака-фактора меняются (в ту или иную строну). При этом признак-результат может реагировать на это изменение по-разному. Явственно и чётко. Или не очень. Или вообще слабо, на грани хаотичной случайности. «Отклик» может быть совершенно разным

И возникает вопрос: насколько СИЛЬНО влияет факторный признак на результат, насколько теснА связь между факторами?

Ответы на этот вопрос дают эмпирический коэффициент детерминации, о котором я уже рассказал в статье о дисперсиях, и связанное с ним эмпирическое корреляционное отношение.

Переходим ко второй части задания, а именно:

2) Измерим тесноту корреляционной связи между стоимостью произведенной продукции и
прибылью с помощью эмпирического корреляционного отношения.

Сначала вычислим эмпирический коэффициент детерминации. Начнём рассуждать неформально: прибыль (признак-результат) варьируется под влиянием самых разных факторов, их может быть довольно много. И общая дисперсия 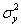учитывает ВСЕ факторы, влияющие на изменение прибыли.

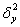
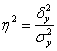
Далее мы разбили совокупность на группы, причём, в основу группировки был положен выпуск продукции (один из факторов). Как вы знаете из предыдущего урока, существенность влияния ЭТОГО фактора измеряется межгрупповой дисперсией . И эмпирический коэффициент детерминации показывает ДОЛЮ влияния группировочного признака – чем ближе этот коэффициент к единице, тем сильнее влияние причины на следствие.

Внимание! Если вам не очень понятно, о чём речь, обязательно изучите предыдущий урок по ссылкам выше!

Собственно, переходим к вычислениям. Общую дисперсию прибыли можно вычислить как по исходным, так и отсортированным данным, это не имеет значения. Я выберу первый вариант. Сначала найдём среднее значение прибыли по все выборке:
млн. руб.

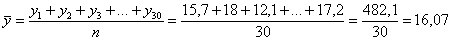
Дисперсию вычислим по определению: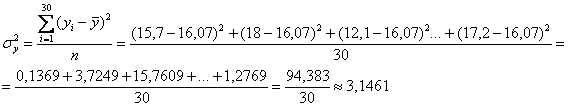

О том, как автоматизировать расчёты в Экселе, я неоднократно рассказывал в своих видеороликах, в частности, на уроке о дисперсиях.

Вычислим межгрупповую дисперсию:

И для очистки совести можно ещё вычислить внутригрупповую дисперсию, чтобы проверить правило сложения дисперсий 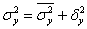и убедиться в правильности выполненных расчётов. Что я и сделал на черновике.

В результате: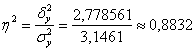
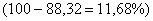
, таким образом, 88,32% вариации прибыли обусловлено стоимостью выпущенной продукции. Оставшаяся часть вариации обусловлена другими факторами.

По коэффициенту 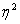можно судить о силе влияния причины на следствие, однако для оценки этой силы существует «специализированный» показатель, а именно:

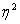
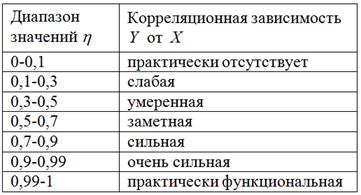
эмпирическое корреляционное отношение, равное квадратному корню из . Фактически это отношение соответствующих стандартных отклонений:

Данное отношение тоже изменяется в пределах 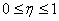, и характеризует тесноту (силу) связи между признаками. Для качественной оценки этой силы часто используют так называемую шкалу Чеддока:

В нашем случае 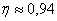, таким образом, прибыль предприятий очень сильно зависит от стоимости выпущенной продукции.

Следует отметить, что результаты подобных задач не являются какой-то «абсолютной истиной» – это всего лишь математическая модель. Так, мы могли выполнить группировку другим способом, разбить выборочную совокупность на иное количество групп, и тогда у нас получились бы другие средние значения прибыли и другие коэффициенты 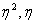. Однако, они вряд ли будут сильно отличаться от полученных результатов, и выводы мы сделаем те же самые. И это действительно так.

Кстати, если вы получили явно сомнительные результаты, то можно попробовать подобрать более удачную группировку, например, укрупнить интервалы и сделать меньше групп или использовать равнонаполненную группировку. В реальных практических исследованиях для повышения репрезентативности целесообразно увеличить объём выборки, т.е. рассмотреть не 30 значений, а 50-100 или даже больше. И в этом нет ничего необычного – ведь первоначальная модель может оказаться неудачной.

Следующее задание для самостоятельного решения:

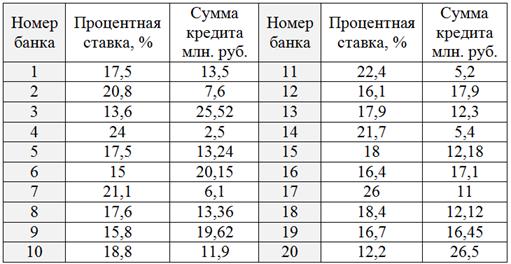
По результатам выборочного исследования 20 банков известны процентные ставки и соответствующие суммы выданных кредитов:

1) Определить факторный и результативный признак и выдвинуть предположение о наличии и направлении корреляционной связи между показателями.

2) Методом аналитической группировки проверить наличие корреляционной связи, выборку разбить на 4 группы с равным количеством банков в каждой. Результаты представить в виде групповой и аналитической таблицы. Сделать выводы.

3) Вычислить эмпирический коэффициент детерминации и эмпирическое корреляционное отношение. Сделать выводы.

Обратите внимание, что во 2-м пункте вам прямо указано, как следует выполнять группировку – в таких случаях не нужно проявлять самодеятельность – строго следуем указаниям условия. А если решение получится не слишком удачное, то это уж проблемы автора задачи.

Все числа забиты в Эксель и вам осталось быстренько выполнить действия. Решение для сверки совсем близко.

Что ещё можно сказать по теме?

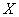
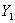
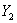
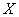
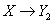
В некоторых задачах результативных признаков может быть несколько, как правило, два, например: – выпуск продукции – прибыль и – себестоимость производства. Никаких проблем – сортируем совокупности по признаку-фактору (выпуску продукции), при этом в Экселе нужно выделить не два, а уже три столбца, о чём я уже рассказывал в ролике. Далее выполняем группировку и рассчитываем средние значения прибыли и себестоимости по каждой группе. Делаем выводы. Заметим, кстати, что корреляционная связь , вероятно, обратная, поскольку при увеличении выпуска продукции, издержки могут падать (ввиду автоматизации процесса при массовом производстве).

И в заключение хочу сказать, что показатели вам могут быть предложены самые разные, поэтому при решении этих задач следует включать голову и элементарную логику.

До скорых встреч!

Решения и ответы:

Пример 62. Решение:

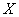
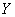
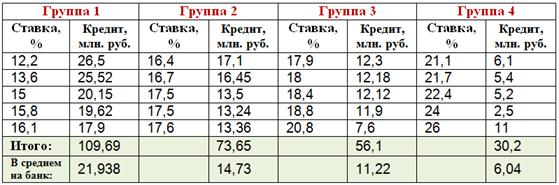
1) Очевидно, что чем больше процентная ставка, тем в среднем будет меньше сумма кредита, поскольку при высоких ставках заёмщику труднее расплачиваться по обязательствам. Таким образом, процентная ставка – признак-фактор, а сумма кредита – признак-результат. Предполагаемая корреляционная зависимость – обратная («чем больше, тем меньше»).

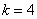
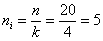
2) Проверим выдвинутое предположение методом аналитической группировки. Упорядочим выборочную совокупность по возрастанию процентной ставки и разобьём её на группы по банков в каждой группе:

По каждой группе вычислим сумму кредитов (графа «Итого») и средние значения кредита 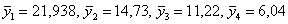млн. руб. (разделив суммы на объёмы групп, то есть на 5).

Результаты сведём в аналитическую таблицу: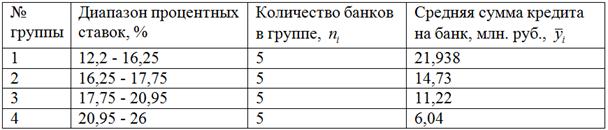

Таким образом, при увеличении процентных ставок средние значения выданных кредитов уменьшаются, что подтверждает обратную корреляционную зависимость суммы кредита от процентной ставки.
3) Найдём эмпирический коэффициент детерминации .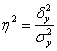
Вычислим общую среднюю (рассчитываю по упорядоченной совокупности):
млн. руб.

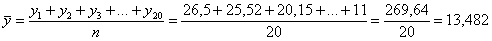
Вычислим общую дисперсию: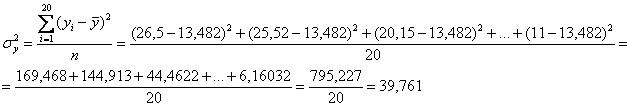

Вычислим межгрупповую дисперсию: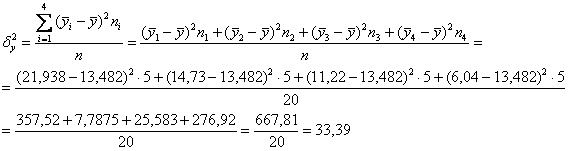

В результате: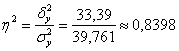
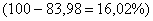
, таким образом, 83,98% вариации размера кредита обусловлено процентной ставкой (группировочным признаком). Оставшаяся часть вариации обусловлена другими факторами.

Вычислим эмпирическое корреляционное отношение:

Таким образом, корреляционная зависимость суммы кредита от процентной ставки является очень сильной.

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник