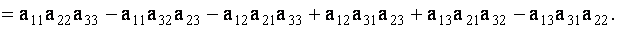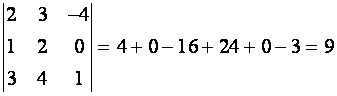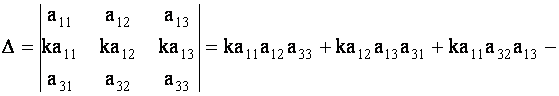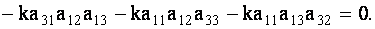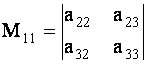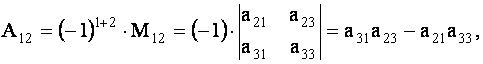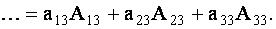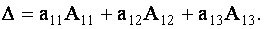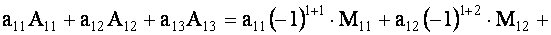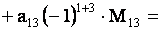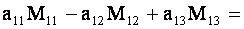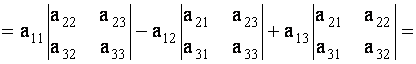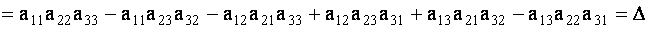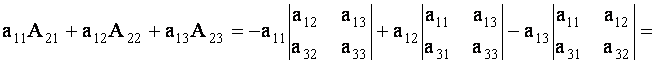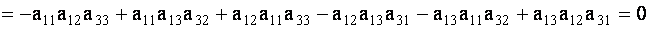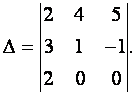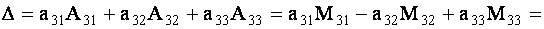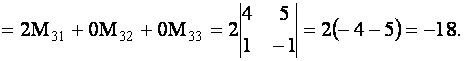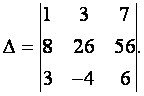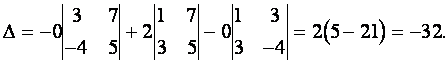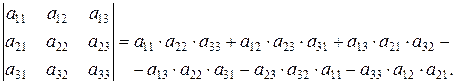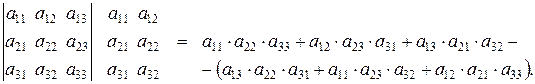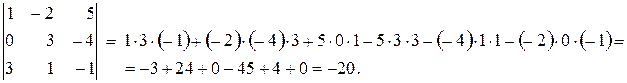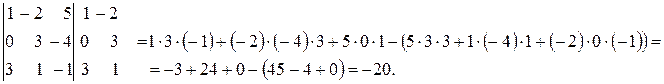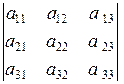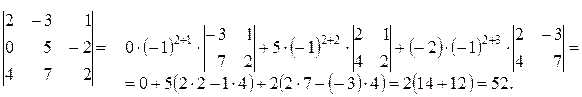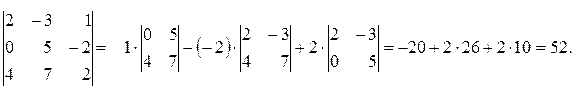Математика — онлайн помощь
Пусть дана квадратная матрица третьего порядка
Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число
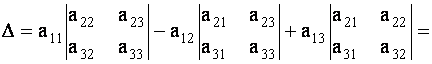 | (1.7) |
Определитель третьего порядка обозначается символом
 | (1.8) |
где числа 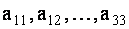
Индексы 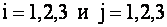
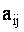
Например, элемент 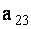
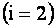
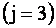
Элементы 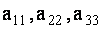
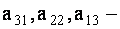
Определение имеет сложный по форме вид, поэтому для нахождения определителя третьего порядка предложены более простые правила. Так, согласно правилу треугольников необходимо:
- вычислить с собственными знаками произведения элементов , лежащих на главной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны этой диагонали ;
- найти произведения элементов, лежащих на побочной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали, и взять их с противоположными знаками ;
- найти общую сумму всех произведений.
Все свойства определителей второго порядка справедливы и для определителей третьего порядка. Доказательства этих свойств основаны на вычислении определителя третьего порядка по формуле (1.7).
Например, покажем, что определитель, у которого элементы двух его строк пропорциональны, равен нулю. Действительно,
Аналогично проверяется справедливость и других свойств.
Пусть дан определитель (1.8) третьего порядка.
ОПРЕДЕЛЕНИЕ 1.9: Минором 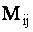
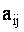
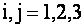
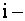
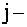
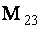
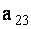
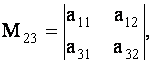
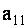
С помощью миноров определитель (7) можно записать в виде
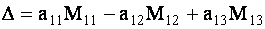 | (1.9) |
ОПРЕДЕЛЕНИЕ 1.10: Алгебраическим дополнением 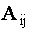
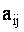
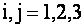
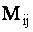
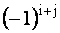
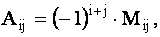 где где 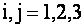 / / | (1.10) |
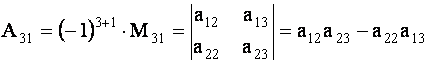
ТЕОРЕМА 1.1 Разложение определителя по элементам строки или столбца
Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения. Иными словами, имеют место шесть равенств:
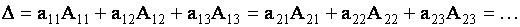 | (1.11) |
Проверим, например, справедливость равенства
Согласно определениям минора и алгебраического дополнения получим
ТЕОРЕМА 1.2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
Для определенности выберем элементы 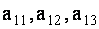
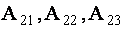
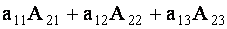
Аналогично проверяется равенство нулю и всех других подобных сумм.
В заключение рассмотрим схему использования свойств определителя и теоремы разложения при вычислении определителя.
Вычислить определитель
Решение. Разложим определитель по элементам третьей строки.
Вычислить определитель
Решение. Прибавляя ко второй строке первую, умноженную на — 8,
получим 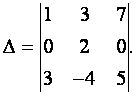
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А = ( a i j ) n × n .
|А|, ∆ , det A — символы, которыми обозначают определитель матрицы.
Способ вычисления определителя выбирают в зависимости от порядка матрицы.
Определитель матрицы 2-го порядка вычисляют по формуле:
d e t A = 1 — 2 3 1 = 1 × 1 — 3 × ( — 2 ) = 1 + 6 = 7
Определитель матрицы 3-го порядка: правило треугольника
Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:
- правило треугольника;
- правило Саррюса.
Как найти определитель матрицы 3-го порядка по методу треугольника?
а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32
А = 1 3 4 0 2 1 1 5 — 1
d e t A = 1 3 4 0 2 1 1 5 — 1 = 1 × 2 × ( — 2 ) + 1 × 3 × 1 + 4 × 0 × 5 — 1 × 2 × 4 — 0 × 3 × ( — 1 ) — 5 × 1 × 1 = ( — 2 ) + 3 + 0 — 8 — 0 — 5 = — 12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32
А = 1 3 4 0 2 1 — 2 5 — 1 1 3 0 2 — 2 5 = 1 × 2 × ( — 1 ) + 3 × 1 × ( — 2 ) + 4 × 0 × 5 — 4 × 2 × ( — 2 ) — 1 × 1 × 5 — 3 × 0 × ( — 1 ) = — 2 — 6 + 0 + 16 — 5 — 0 = 3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.
Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение матрицы по элементам строки:
d e t A = a i 1 × A i 1 + a i 2 × A i 2 + . . . + а i n × А i n
Разложение матрицы по элементам столбца:
d e t A = а 1 i × А 1 i + а 2 i × А 2 i + . . . + а n i × А n i
Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0
- раскладываем по 2-ой строке:
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 2 × ( — 1 ) 3 × 1 — 1 3 — 2 5 1 3 1 0 = — 2 × 1 — 1 3 4 5 1 2 1 0 + 1 × 0 — 1 3 — 2 5 1 3 1 0
- раскладываем по 4-му столбцу:
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 3 × ( — 1 ) 5 × 2 1 0 — 2 4 5 3 2 1 + 1 × ( — 1 ) 7 × 0 1 — 1 2 1 0 3 2 1 = — 3 × 2 1 0 — 2 4 5 3 2 1 — 1 × 0 1 — 1 2 1 0 3 2 1
Свойства определителя
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
Пример 6
А = 1 3 4 0 2 1 0 0 5
d e t А = 1 3 4 0 2 1 0 0 5 = 1 × 5 × 2 = 10
Определитель матрицы, который содержит нулевой столбец, равняется нулю.
Источник
Методы вычисления определителя третьего порядка
Определители и способы их вычисления
Определитель – это число, соответствующее квадратной матрице, вычисленное определенным образом.
Определителем второго порядка называется число, определяемое равенством:
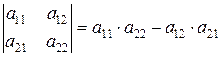
Пример 3.1.
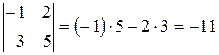
Определителем третьего порядка называется число, определяемое квадратной матрицей третьего порядка.
1.Метод треугольников (метод Саррюса)
То есть, если элементы определителя третьего порядка записать в таблицу 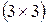
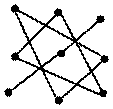 |
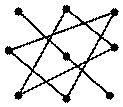 |
| Рис. 1 |
Это правило называется правилом Саррюса.
2. Метод дописывания двух столбцов.
Этот способ вычисления определителя третьего порядка заключается в дописывании первых двух столбцов определителя и нахождении суммы произведений по главной диагонали и параллелях к ней за вычетом суммы произведений побочной диагонали и параллелях к ней, т.е.
Пример 3.2. Вычислить определитель двумя способами
3. Третий способ вычисления определителя основан на теореме разложения.
Минором элемента определителя 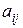
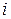
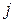
Например, минором элемента 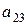
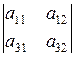
т.е. из исходного определителя были вычеркнуты вторая строка и третий столбец.
Алгебраическим дополнением 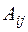
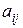
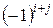
При этом полезно иметь в виду следующую схему:
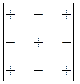 | где знаком плюс отмечены места тех элементов, для которых алгебраические дополнения равны минорам, взятым с их собственным знаком; и знаком минус те, для которых алгебраические дополнения равны минорам, взятым с противоположным знаком. |
| Теорема разложения | Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения. |
Пример 3.3. Вычислить определитель путем разложения: а) по второй строке; б) по третьему столбцу.
а)
б)
Замечание. Если в задании не указано, по какому столбцу (строке) проводить разложение, то лучше выбирать столбец (строку) с большим числом нулей.
Определитель 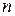
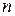
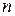
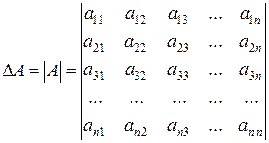
Вычисление определителей порядка больше 3, рекомендуется проводить с помощью теоремы разложения.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник