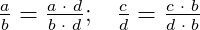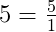Как сравнивать дроби удобным способом

Сравнение дробей: правила, примеры, решения.

В центре внимания данной статьи стоит сравнение дробей. Мы уже знаем про равные и неравные дроби. Две неравные дроби подлежат дальнейшему сравнению для выяснения, какая дробь больше, а какая дробь меньше. Для сравнения двух дробей существует правило сравнения дробей, которое мы сформулируем ниже, а также разберем примеры применения этого правила при сравнении дробей с одинаковыми и разными знаменателями. В заключение покажем, как сравнить дроби с одинаковыми числителями, не приводя их к общему знаменателю, а также рассмотрим, как сравнить обыкновенную дробь с натуральным числом.

Навигация по странице.

Сравнение дробей с одинаковыми знаменателями

Сравнение дробей с одинаковыми знаменателями по сути является сравнением количества одинаковых долей. К примеру, обыкновенная дробь 3/7 определяет 3 доли 1/7 , а дробь 8/7 соответствует 8 долям 1/7 , поэтому сравнение дробей с одинаковыми знаменателями 3/7 и 8/7 сводится к сравнению чисел 3 и 8 , то есть, к сравнению числителей.

Из этих соображений вытекает правило сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше.

Озвученное правило объясняет, как сравнить дроби с одинаковыми знаменателями. Рассмотрим пример применения правила сравнения дробей с одинаковыми знаменателями.

Какая дробь больше: 65/126 или 87/126 ?

Знаменатели сравниваемых обыкновенных дробей равны, а числитель 87 дроби 87/126 больше числителя 65 дроби 65/126 (при необходимости смотрите сравнение натуральных чисел). Поэтому, согласно правилу сравнения дробей с одинаковыми знаменателями, дробь 87/126 больше дроби 65/126 .

.

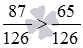
Сравнение дробей с разными знаменателями

Сравнение дробей с разными знаменателями можно свести к сравнению дробей с одинаковыми знаменателями. Для этого лишь нужно сравниваемые обыкновенные дроби привести к общему знаменателю.

Итак, чтобы сравнить две дроби с разными знаменателями, нужно

• привести дроби к общему знаменателю;
• сравнить полученные дроби с одинаковыми знаменателями.

Разберем решение примера.

Сравните дробь 5/12 с дробью 9/16 .

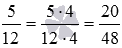
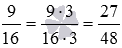
Сначала приведем данные дроби с разными знаменателями к общему знаменателю (смотрите правило и примеры приведения дробей к общему знаменателю). В качестве общего знаменателя возьмем наименьший общий знаменатель, равный НОК(12, 16)=48 . Тогда дополнительным множителем дроби 5/12 будет число 48:12=4 , а дополнительным множителем дроби 9/16 будет число 48:16=3 . Получаем и .

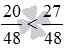
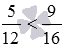
Сравнив полученные дроби, имеем . Следовательно, дробь 5/12 меньше, чем дробь 9/16 . На этом сравнение дробей с разными знаменателями завершено.

.

Получим еще один способ сравнения дробей с разными знаменателями, который позволит выполнять сравнение дробей без их приведения к общему знаменателю и всех сложностей, связанных с этим процессом.

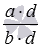
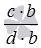
Для сравнения дробей a/b и c/d , их можно привести к общему знаменателю b·d , равному произведению знаменателей сравниваемых дробей. В этом случае дополнительными множителями дробей a/b и c/d являются числа d и b соответственно, а исходные дроби приводятся к дробям и с общим знаменателем b·d . Вспомнив правило сравнения дробей с одинаковыми знаменателями, заключаем, что сравнение исходных дробей a/b и c/d свелось к сравнению произведений a·d и c·b .

Отсюда вытекает следующее правило сравнения дробей с разными знаменателями: если a·d>b·c , то 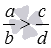, а если a·d , то .

Рассмотрим сравнение дробей с разными знаменателями этим способом.

Сравните обыкновенные дроби 5/18 и 23/86 .

В этом примере a=5 , b=18 , c=23 и d=86 . Вычислим произведения a·d и b·c . Имеем a·d=5·86=430 и b·c=18·23=414 . Так как 430>414 , то дробь 5/18 больше, чем дробь 23/86 .

.

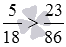
Сравнение дробей с одинаковыми числителями

Дроби с одинаковыми числителями и разными знаменателями, несомненно, можно сравнивать с помощью правил, разобранных в предыдущем пункте. Однако, результат сравнения таких дробей легко получить, сравнив знаменатели этих дробей.

Существует такое правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель, и меньше та дробь, знаменатель которой больше.

Рассмотрим решение примера.

Сравните дроби 54/19 и 54/31 .

Так как числители сравниваемых дробей равны, а знаменатель 19 дроби 54/19 меньше знаменателя 31 дроби 54/31 , то 54/19 больше 54/31 .

.

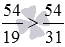
В заключение этого пункта приведем пример, хорошо иллюстрирующий основную суть озвученного правила сравнения дробей с одинаковыми числителями. Пусть перед нами две тарелки, на одной из них 1/2 пирога, а на другой 1/16 этого же пирога. Понятно, что скушав половину пирога, мы будем куда больше сыты, чем съев 1/16 его часть.

Сравнение дроби с натуральным числом

Сравнение обыкновенной дроби с натуральным числом сводится к сравнению двух дробей, если число записать в виде дроби со знаменателем 1 (смотрите натуральное число как дробь со знаменателем 1). Рассмотрим решение примера.

Сравните дробь 63/8 и число 9 .

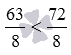
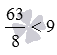
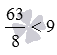
Число 9 можно представить как дробь 9/1 , этим сравнение дроби 63/8 и числа 9 сводится к сравнению дробей 63/8 и 9/1 . После их приведения к общему знаменателю 8 , получаем дроби с одинаковым знаменателем 63/8 и 72/8 . Так как 63 , то , следовательно, .

.

Источник

Сравнение обыкновенных дробей

Сравнить две дроби — значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.

Сравнение дробей с одинаковыми знаменателями

Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

Пример. Дробь 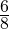больше чем дробь , потому что доли в обеих дробях одинаковы, но в первой дроби их больше, чем во второй.

Если изобразим единицу отрезком и разделим его на 8 долей, то легко увидеть, что дробь 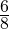больше :

Сравнение дробей с одинаковыми числителями

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.

Пример. Дробь 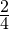больше чем дробь , потому что число долей в обеих дробях одинаково, но в первой дроби доли крупнее, чем во второй.

Изобразим две единицы в виде кругов, один разделим на 4 доли, второй на 6 долей. Теперь можно увидеть, что дробь 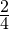больше :

Сравнение дробей с разными знаменателями и числителями

Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дроби: и .

Решение: приводим данные дроби к общему знаменателю:

Теперь сравниваем их по правилу сравнения дробей, у которых одинаковые знаменатели. Так как 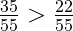, значит .

Приведём ещё один способ сравнения дробей с разными знаменателями и числителями. Рассмотрим сначала числовой пример.

Пример. Сравним дроби и .

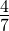
Решение: приводим данные дроби к общему знаменателю:

Решая данный пример можно заметить, что, после приведения дробей к общему знаменателю, задача сравнения свелась фактически к сравнению произведений

Так как 2 · 7 = 14, а 4 · 3 = 12, то

Значит, .

Теперь решим эту же задачу в общем виде, используя буквенную запись.

Пример. Пусть даны дроби и , где a и c — нуль или натуральные числа, b и d — натуральные числа. Приведём дроби к общему знаменателю:

1. если a · d >c · b, то
2. если a · d Пример.

Сравнение неправильной дроби с натуральным числом сводится к сравнению двух дробей.

Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби со знаменателем 1, затем их можно сравнить одним из двух способов: используя перекрёстное правило, либо привести дроби к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дробь с числом 5.

Решение: представим число 5 в виде дроби со знаменателем 1:

Приводим дроби к общему знаменателю:

Сравниваем числители, так как 11 Пример.

Онлайн калькулятор сравнения дробей

Данный калькулятор поможет вам сравнить обыкновенные дроби. Просто введите две дроби и нажмите кнопку Сравнить .

Источник

Сравнение дробей

Также как и натуральные числа обыкновенные дроби можно сравнивать.

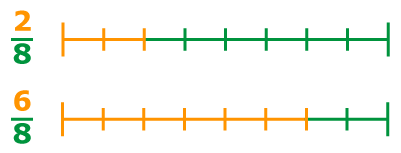
Рассмотрим две неравные дроби на числовой оси. Меньшая дробь будет располагаться левее, а большая — правее.

Равные дроби соответствует одной и той же точке на числовой оси.

На рисунке хорошо видно, что

1

5

. Но необязательно пользоваться числовой осью, чтобы сравнивать дроби.

Сравнение дробей с одинаковыми знаменателями

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Пример. Сравним

1

5

и

4

5

.

В обеих дробях одинаковый знаменатель равный 5 .

В первой дроби числитель равен 1 и он меньше числителя второй дроби, который равен 4 .

Поэтому первая дробь

1

5

меньше второй

4

5

.

Сравнение дробей с одинаковыми числителями

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Пример. Сравним

1

2

и

1

8

. Ответ:

Правило выше легче понять, если представить, что у вас в руках куски торта. В первом случае торт разделили на 2 части (знаменатель дроби равен 2 ), и у вас в руках половина торта, а во втором — торт поделили на 8 частей, и у вас в руках маленькая часть торта.

Сравнение дробей с разными знаменателями

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.

После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей с одинаковыми знаменателями.

Пример. Сравним

2

7

и

1

14

.

• Приводим дроби к общему знаменателю.
• Сравниваем дроби с одинаковыми знаменателями.

Любая неправильная дробь больше любой правильной.

Это объясняется тем, что неправильная дробь всегда больше или равна 1 , а правильная дробь всегда меньше 1 .

Источник