Как создать свой способ шифрования

10 популярных кодов и шифров

Авторизуйтесь

10 популярных кодов и шифров

Коды и шифры — не одно и то же: в коде каждое слово заменяется другим, в то время как в шифре заменяются все символы сообщения.

В данной статье мы рассмотрим наиболее популярные способы шифрования, а следующим шагом будет изучение основ криптографии.

Стандартные шифры

Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, А заменяется на Б, Б — на В, и т. д. Фраза «Уйрйшоьк Рспдсбннйту» — это «Типичный Программист».

Попробуйте расшифровать сообщение:

Сумели? Напишите в комментариях, что у вас получилось.

Шифр транспонирования

В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из hello world получается dlrow olleh. Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl.

Ещё можно использовать столбчатый шифр транспонирования, в котором каждый символ написан горизонтально с заданной шириной алфавита, а шифр создаётся из символов по вертикали. Пример:

Из этого способа мы получим шифр holewdlo lr. А вот столбчатая транспозиция, реализованная программно:

Азбука Морзе

В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов:
Чаще всего это шифрование передаётся световыми или звуковыми сигналами.

Сможете расшифровать сообщение, используя картинку?

Шифр Цезаря

Это не один шифр, а целых 26, использующих один принцип. Так, ROT1 — лишь один из вариантов шифра Цезаря. Получателю нужно просто сообщить, какой шаг использовался при шифровании: если ROT2, тогда А заменяется на В, Б на Г и т. д.

А здесь использован шифр Цезаря с шагом 5:

Моноалфавитная замена

Коды и шифры также делятся на подгруппы. Например, ROT1, азбука Морзе, шифр Цезаря относятся к моноалфавитной замене: каждая буква заменяется на одну и только одну букву или символ. Такие шифры очень легко расшифровываются с помощью частотного анализа.

Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».

Однако этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов.

Шифр Виженера

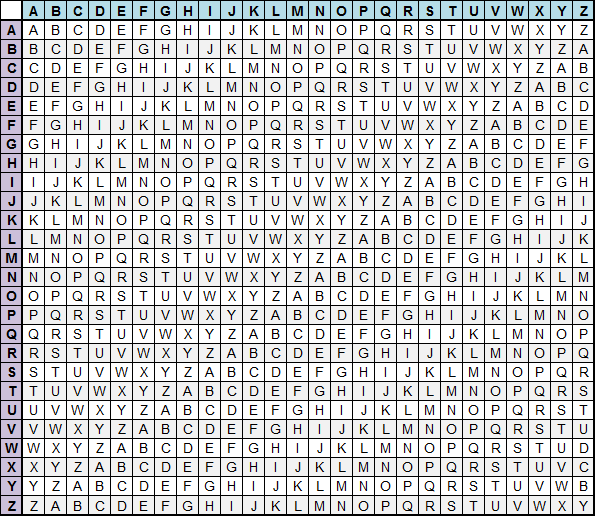
Представим, что есть таблица по типу той, что на картинке, и ключевое слово «CHAIR». Шифр Виженера использует принцип шифра Цезаря, только каждая буква меняется в соответствии с кодовым словом.

В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова «С», вторая буква — для «H», etc. Если послание длиннее кодового слова, то для (k*n+1)-ой буквы, где n — длина кодового слова, вновь будет использован алфавит для первой буквы кодового слова.

Чтобы расшифровать шифр Виженера, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания.

Попробуйте расшифровать эту фразу самостоятельно:

Подсказка длина кодового слова — 4.

Шифр Энигмы

Энигма — это машина, которая использовалась нацистами во времена Второй Мировой для шифрования сообщений.

Есть несколько колёс и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.

Существовало более ста триллионов возможных комбинаций колёс, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.

Цифровые шифры

В отличие от шифровки текста алфавитом и символами, здесь используются цифры. Рассказываем о способах и о том, как расшифровать цифровой код.

Двоичный код

Текстовые данные вполне можно хранить и передавать в двоичном коде. В этом случае по таблице символов (чаще всего ASCII) каждое простое число из предыдущего шага сопоставляется с буквой: 01100001 = 97 = «a», 01100010 = 98 = «b», etc. При этом важно соблюдение регистра.

Расшифруйте следующее сообщение, в котором использована кириллица:

Шифр A1Z26

Это простая подстановка, где каждая буква заменена её порядковым номером в алфавите. Только нижний регистр.

Попробуйте определить, что здесь написано:

Шифрование публичным ключом

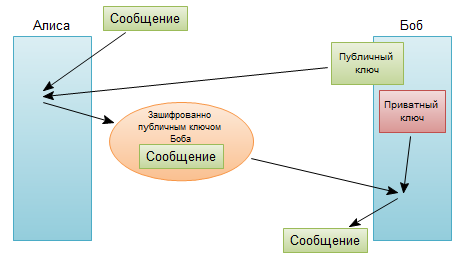
Алгоритм шифрования, применяющийся сегодня буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53.

Открытый ключ используется, чтобы зашифровать сообщение, а секретный — чтобы расшифровать.

Как-то RSA выделила 1000 $ в качестве приза тому, кто найдет два пятидесятизначных делителя числа:

Как расшифровать код или шифр?

Для этого применяются специальные сервисы. Выбор такого инструмента зависит от того, что за код предстоит расшифровать. Примеры шифраторов и дешифраторов:

Источник

Разработка собственного алгоритма симметричного шифрования на Php

Однажды, несколько лет назад, доводилось делать тестовое задание для трудоустройства на работу в одну компанию, где в качестве задания стояла задача разработать нестандартный алгоритм симметричного шифрования на высокоуровневом яп, идейно в чем-то непохожий на классику жанра — операцию xor исходного сообщения и секретного ключа. Задание было худо бедно сделано, но сама идея создания интересного нетривиального алгоритма засела в голове надолго.

И, на данный момент из нее получилось то, что я назвал GenCoder.

Предвосхищая комментарии про особые органы и аспекты взаимоотношения с ними, в случае, если деятельность имеет отношение к криптографии, забегая вперед, скажу, что работа ведется исключительно в экспериментальных и исследовательских (некоммерческих) целях.

Собственно, исходный код класса можно посмотреть здесь, а потестировать можно тут.

Итак, задача (данного исследовательского эксперимента, так его назовем) стояла следующая:

Разработать собственный алгоритм обратимого шифрования, притом что:

• Каждый раз одно и то же сообщение будет зашифровываться уникальным образом и не повторяться.
• Внедрить так называемую «рандомизацию» секретного ключа — найти способ как шифровать сообщения не постоянно одним и тем же секретным ключом, а некой секретной строкой, являющейся функцией от секретного ключа и исходного сообщения.
• Как маловажное дополнение, сделать переменным по длине секретный ключ при с сохранением высокой криптостойкости алгоритма (в текущей версии — от 64 до 100 символов).
• Как было сказано выше, не привязываться к существующим решениям, а сделать нечто свое, без сложной математики, с простым и понятным алгоритмом.

Для разработки было выбрано симметричное шифрование.

Как правило, реализации симметричного шифрования обычно делятся на две большие категории, блочные шифры и поточные шифры. Блочные шифры шифруют исходное сообщение небольшими блоками, поточные шифры шифруют сообщение целиком сопоставляя его с некой гаммой, то есть, важно также местоположение символа сообщения в исходном сообщении. Немного неуклюже сказано и на определение явно не тянет, но зато максимально доходчиво.

Описываемый здесь алгоритм более похож на поточный шифр, хотя не является им в чистом виде.

Задумывая реализацию алгоритма, в самых общих чертах было понимание, что секретный ключ должен быть лишь одним из элементов финального аккорда в симфонии шифрования, но не самим этим аккордом. То есть в идеале, говоря образно, каждое сообщение должно по хорошему как бы само шифровать себя, а ключ должен быть лишь некой стартовой точкой этого алгоритма, если хотите, неким инициализирующим вектором.

Основная идея прелесть получившегося алгоритма заключается в том, что для каждого акта шифрования не используется один и тот же секретный ключ, а генерируется функция обхода исходного ключа, так называемая сигнатура пути обхода (pathKeySignature в коде), причем функция зависит от нескольких аргументов. А именно — от сложной комбинации sha-512 хешей соли приложения, исходного сообщения, уникального идентификатора uniqid, а также от хешкодов отправителя и получателя сообщения.

Что такое сигнатура обхода ключа на пальцах? Если упростить, это фактически алгоритм обхода ключа. Например, берем первый символ ключа, затем 14-ый, затем 22-ой, затем 37-ой, затем 49-ый и т.д. Каждый новый такой обход — уникален (в силу уникальности генерируемого pathKeySignature).

Кроме того, в алгоритм внесены элементы двухфакторного шифрования (более подходящего термина не нашел, речь идет о коротких пин-паролях у отправителя и получателя, подробнее ниже по тексту). Далее, непосредственно «под капотом» используется обычный xor-метод.

«Двухфакторность» проявляется в том, что для генерации сигнатуры пути используются небольшие пароли (pass1 и pass2, по 4 символа), притом, что получателю неизвестен пароль отправителя, а отправителю неизвестен пароль получателя, но притом они обмениваются функциями-хешкодами от соли приложения и пароля второй стороны.

Использование вышеописанных методов позволяет сделать достаточно сложной и трудно подбираемой функцию обхода ключа. А точнее, она каждый раз будет уникальна даже для одного и того же исходного сообщения, так что хочется надеяться стандартные методы криптоанализа (например, известный метод частотного анализа) здесь окажутся бессильными.

Предварительно магия начинается здесь.

Собственно, наличие md5 хеш-функции может поначалу немного смутить, но этот элемент алгоритма отвечает лишь только за внесение хаотичности, лавинности изменений (как и sha512) в генерируемый attachKey. Функция uniqid отдает нам уникальный идентификатор, что по итогу позволяет шифровать одно и то же исходное сообщение каждый раз новым шифром, что в конечном счете гуд. Зачем так заморачиваться? Представьте, что вы разрабатываете свой месседжер с шифрованием. Шифрование одних и тех же сообщений одним и тем же конечным шифром — если не прямая уязвимость, то явный шаг в ее сторону. Почему? Как правило, в данном контексте пользователи обмениваются весьма однотипным набором данных, из серии «привет!», «я понял», «ок», «скоро буду», «как дела?». Допустим, к примеру, у нас такой месседжер. Канал шифрования установлен, пользователь 1 отправил пользователю 2 шифрованное сообщение «0372985dee«, пользователь 2 прочел сообщение и через 5 секунд ответил «0372985dee» обратно. Что зашифровано там? Ответ почти очевиден.
Это было лирическое отступление на тему уместности uniqid, возвращаемся к коду.

Магия продолжается здесь. Собственно, здесь в методе cipher происходит непосредственно обход ключа посредством сигнатуры $path_key_signature, а метод byteShifting дополнительно вносит хаотичность в генерируемый шифр посредством добавления различных сдвигов в определенных границах.

Непосредственно в публичном методе шифрования не так много интересного, ибо все интересное а ля создание присоединяемого хеша attachKey и генерация пути обхода pathKeySignature описаны выше. Разве что, стоит отметить, что к выходящему наружу в незащищенный канал шифру конкатенируется $attach_key

Возможно, возникнет резонный вопрос. Почему бы не ограничиться в функции пути обхода просто одним attachKey, для чего добавлять туда хешкоды отправителя и получателя? Ответ находится тут же, «рядом» — attachKey расположен фактически на виду в создаваемом шифре, и зная его, не составляет труда реконструировать последовательность прохождения ключа при шифре. Сам секретный ключ это, разумеется, напрямую восстановить не даст, но сведет на нет всю идею «рандомизации» ключа. Поэтому, нужен дополнительный фактор, которым являются хешкоды получателей. Они представляют собой своего рода второй секретный элемент алгоритма помимо ключа. Этакое своего рода двухфакторное шифрование.

Метод decodeMessage детально рассматривать не будем, он практически тривиален, если учитывать полную симметричность с методом шифрования только в обратной последовательности.

Алгоритм выглядит вполне законченным, по крайней мере для некоего теоретического эксперимента.

• Относительно быстр по скорости шифрования/дешифрования (об этом ниже)
• Прост и понятен
• Открыт для изучения и улучшения, ибо опенсорс

• (скорее обстоятельство, чем недостаток) Требуется детальный анализ, чтобы понимать насколько он криптографически стоек.

В двух словах по поводу тестирования.

По скорости работы алгоритма — относительно быстр (разумеется, все относительно и познается в сравнении, речь о скорости шифрования в рамках высокоуровнего яп вообще и в рамках php в частности). 2 мегабайта рандомного текста было зашифровано и расшифровано за 4 секунды, использовался при этом php 7.2. Система: Intel Core i7-8700 CPU @ 3.20GHz × 12, параллельно еще работал браузер с кучей вкладок и виртуальная машина. Резюме — скорость шифрования

1 мб/сек на среднестатистическом железе на php7.0 и выше.

Источник

Классический криптоанализ

На протяжении многих веков люди придумывали хитроумные способы сокрытия информации — шифры, в то время как другие люди придумывали еще более хитроумные способы вскрытия информации — методы взлома.

В этом топике я хочу кратко пройтись по наиболее известным классическим методам шифрования и описать технику взлома каждого из них.

Шифр Цезаря

Самый легкий и один из самых известных классических шифров — шифр Цезаря отлично подойдет на роль аперитива.
Шифр Цезаря относится к группе так называемых одноалфавитных шифров подстановки. При использовании шифров этой группы «каждый символ открытого текста заменяется на некоторый, фиксированный при данном ключе символ того же алфавита» wiki.

Способы выбора ключей могут быть различны. В шифре Цезаря ключом служит произвольное число k, выбранное в интервале от 1 до 25. Каждая буква открытого текста заменяется буквой, стоящей на k знаков дальше нее в алфавите. К примеру, пусть ключом будет число 3. Тогда буква A английского алфавита будет заменена буквой D, буква B — буквой E и так далее.

Для наглядности зашифруем слово HABRAHABR шифром Цезаря с ключом k=7. Построим таблицу подстановок:

a

b

c

d

e

f

g

h

i

j

k

l

m

n

o

p

q

r

s

t

u

v

w

x

y

z

h

i

j

k

l

m

n

o

p

q

r

s

t

u

v

w

x

y

z

a

b

c

d

e

f

g

И заменив каждую букву в тексте получим: C(‘HABRAHABR’, 7) = ‘OHIYHOHIY’.

При расшифровке каждая буква заменяется буквой, стоящей в алфавите на k знаков раньше: D(‘OHIYHOHIY’, 7) = ‘HABRAHABR’.

Криптоанализ шифра Цезаря

Малое пространство ключей (всего 25 вариантов) делает брут-форс самым эффективным и простым вариантом атаки.
Для вскрытия необходимо каждую букву шифртекста заменить буквой, стоящей на один знак левее в алфавите. Если в результате этого не удалось получить читаемое сообщение, то необходимо повторить действие, но уже сместив буквы на два знака левее. И так далее, пока в результате не получится читаемый текст.

Аффиный шифр

Рассмотрим немного более интересный одноалфавитный шифр подстановки под названием аффиный шифр. Он тоже реализует простую подстановку, но обеспечивает немного большее пространство ключей по сравнению с шифром Цезаря. В аффинном шифре каждой букве алфавита размера m ставится в соответствие число из диапазона 0… m-1. Затем при помощи специальной формулы, вычисляется новое число, которое заменит старое в шифртексте.

Процесс шифрования можно описать следующей формулой:

,

где x — номер шифруемой буквы в алфавите; m — размер алфавита; a, b — ключ шифрования.

Для расшифровки вычисляется другая функция:

,

где a -1 — число обратное a по модулю m. Это значит, что для корректной расшифровки число a должно быть взаимно простым с m.

С учетом этого ограничения вычислим пространство ключей аффиного шифра на примере английского алфавита. Так как английский алфавит содержит 26 букв, то в качестве a может быть выбрано только взаимно простое с 26 число. Таких чисел всего двенадцать: 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23 и 25. Число b в свою очередь может принимать любое значение в интервале от 0 до 25, что в итоге дает нам 12*26 = 312 вариантов возможных ключей.

Криптоанализ аффиного шифра

Очевидно, что и в случае аффиного шифра простейшим способом взлома оказывается перебор всех возможных ключей. Но в результате перебора получится 312 различных текстов. Проанализировать такое количество сообщений можно и в ручную, но лучше автоматизировать этот процесс, используя такую характеристику как частота появления букв.

Давно известно, что буквы в естественных языках распределены не равномерно. К примеру, частоты появления букв английского языка в текстах имеют следующие значения:

Т.е. в английском тексте наиболее встречающимися буквами будут E, T, A. В то время как самыми редкими буквами являются J, Q, Z. Следовательно, посчитав частоту появления каждой буквы в тексте мы можем определить насколько частотная характеристика текста соответствует английскому языку.

Для этого необходимо вычислить значение:

,

где n_i — частота i-й буквы алфавита в естественном языке. И f_i — частота i-й буквы в шифртексте.

Чем больше значение χ, тем больше вероятность того, что текст написан на естественном языке.

Таким образом, для взлома аффиного шифра достаточно перебрать 312 возможных ключей и вычислить значение χ для полученного в результате расшифровки текста. Текст, для которого значение χ окажется максимальным, с большой долей вероятности и является зашифрованным сообщением.

Разумеется следует учитывать, что метод не всегда работает с короткими сообщениями, в которых частотные характеристики могут сильно отличатся от характеристик естественного языка.

Шифр простой замены

Очередной шифр, относящийся к группе одноалфавитных шифров подстановки. Ключом шифра служит перемешанный произвольным образом алфавит. Например, ключом может быть следующая последовательность букв: XFQABOLYWJGPMRVIHUSDZKNTEC.

При шифровании каждая буква в тексте заменяется по следующему правилу. Первая буква алфавита замещается первой буквой ключа, вторая буква алфавита — второй буквой ключа и так далее. В нашем примере буква A будет заменена на X, буква B на F.

При расшифровке буква сперва ищется в ключе и затем заменяется буквой стоящей в алфавите на той же позиции.

Криптоанализ шифра простой замены

Пространство ключей шифра простой замены огромно и равно количеству перестановок используемого алфавита. Так для английского языка это число составляет 26! = 2 88 . Разумеется наивный перебор всех возможных ключей дело безнадежное и для взлома потребуется более утонченная техника, такая как поиск восхождением к вершине:

1. Выбирается случайная последовательность букв — основной ключ. Шифртекст расшифровывается с помощью основного ключа. Для получившегося текста вычисляется коэффициент, характеризующий вероятность принадлежности к естественному языку.
2. Основной ключ подвергается небольшим изменениям (перестановка двух произвольно выбранных букв). Производится расшифровка и вычисляется коэффициент полученного текста.
3. Если коэффициент выше сохраненного значения, то основной ключ заменяется на модифицированный вариант.
4. Шаги 2-3 повторяются пока коэффициент не станет постоянным.

Для вычисления коэффициента используется еще одна характеристика естественного языка — частота встречаемости триграмм.
Чем ближе текст к английскому языку тем чаще в нем будут встречаться такие триграммы как THE, AND, ING. Суммируя частоты появления в естественном языке всех триграмм, встреченных в тексте получим коэффициент, который с большой долей вероятности определит текст, написанный на естественном языке.

Шифр Полибия

Еще один шифр подстановки. Ключом шифра является квадрат размером 5*5 (для английского языка), содержащий все буквы алфавита, кроме J.

При шифровании каждая буква исходного текста замещается парой символов, представляющих номер строки и номер столбца, в которых расположена замещаемая буква. Буква a будет замещена в шифртексте парой BB, буква b — парой EB и так далее. Так как ключ не содержит букву J, перед шифрованием в исходном тексте J следует заменить на I.

Например, зашифруем слово HABRAHABR. C(‘HABRAHABR’) = ‘AB BB EB DA BB AB BB EB DA’.

Криптоанализ шифра Полибия

Шифр имеет большое пространство ключей (25! = 2 83 для английского языка). Однако единственное отличие квадрата Полибия от предыдущего шифра заключается в том, что буква исходного текста замещается двумя символами.

Поэтому для атаки можно использовать методику, применяемую при взломе шифра простой замены — поиск восхождением к вершине.
В качестве основного ключа выбирается случайный квадрат размером 5*5. В ходе каждой итерации ключ подвергается незначительным изменениям и проверяется насколько распределение триграмм в тексте, полученном в результате расшифровки, соответствует распределению в естественном языке.

Перестановочный шифр

Помимо шифров подстановки, широкое распространение также получили перестановочные шифры. В качестве примера опишем Шифр вертикальной перестановки.

В процессе шифрования сообщение записывается в виде таблицы. Количество колонок таблицы определяется размером ключа. Например, зашифруем сообщение WE ARE DISCOVERED. FLEE AT ONCE с помощью ключа 632415.

Так как ключ содержит 6 цифр дополним сообщение до длины кратной 6 произвольно выбранными буквами QKJEU и запишем сообщение в таблицу, содержащую 6 колонок, слева направо:

Для получения шифртекста выпишем каждую колонку из таблицы в порядке, определяемом ключом: EVLNE ACDTK ESEAQ ROFOJ DEECU WIREE.

При расшифровке текст записывается в таблицу по колонкам сверху вниз в порядке, определяемом ключом.

Криптоанализ перестановочного шифра

Лучшим способом атаки шифра вертикальной перестановки будет полный перебор всех возможных ключей малой длины (до 9 включительно — около 400 000 вариантов). В случае, если перебор не дал желаемых результатов, можно воспользоваться поиском восхождением к вершине.

Для каждого возможного значения длины осуществляется поиск наиболее правдоподобного ключа. Для оценки правдоподобности лучше использовать частоту появления триграмм. В результате возвращается ключ, обеспечивающий наиболее близкий к естественному языку текст расшифрованного сообщения.

Шифр Плейфера

Шифр Плейфера — подстановочный шифр, реализующий замену биграмм. Для шифрования необходим ключ, представляющий собой таблицу букв размером 5*5 (без буквы J).

Процесс шифрования сводится к поиску биграммы в таблице и замене ее на пару букв, образующих с исходной биграммой прямоугольник.
Рассмотрим, в качестве примера следующую таблицу, образующую ключ шифра Плейфера:

Зашифруем пару ‘WN’. Буква W расположена в первой строке и первой колонке. А буква N находится во второй строке и третьей колонке. Эти буквы образуют прямоугольник с углами W-E-S-N. Следовательно, при шифровании биграмма WN преобразовывается в биграмму ES.
В случае, если буквы расположены в одной строке или колонке, результатом шифрования является биграмма расположенная на одну позицию правее/ниже. Например, биграмма NG преобразовывается в биграмму GP.

Криптоанализ шифра Плейфера

Так как ключ шифра Плейфера представляет собой таблицу, содержащую 25 букв английского алфавита, можно ошибочно предположить, что метод поиска восхождением к вершине — лучший способ взлома данного шифра. К сожалению, этот метод не будет работать. Достигнув определенного уровня соответствия текста, алгоритм застрянет в точке локального максимума и не сможет продолжить поиск.
Чтобы успешно взломать шифр Плейфера лучше воспользоваться алгоритмом имитации отжига.

Отличие алгоритма имитации отжига от поиска восхождением к вершине заключается в том, что последний на пути к правильному решению никогда не принимает в качестве возможного решения более слабые варианты. В то время как алгоритм имитации отжига периодически откатывается назад к менее вероятным решениям, что увеличивает шансы на конечный успех.

Суть алгоритма сводится к следующим действиям:

1. Выбирается случайная последовательность букв — основной-ключ. Шифртекст расшифровывается с помощью основного ключа. Для получившегося текста вычисляется коэффициент, характеризующий вероятность принадлежности к естественному языку.
2. Основной ключ подвергается небольшим изменениям (перестановка двух произвольно выбранных букв, перестановка столбцов или строк). Производится расшифровка и вычисляется коэффициент полученного текста.
3. Если коэффициент выше сохраненного значения, то основной ключ заменяется на модифицированный вариант.
4. В противном случае замена основного ключа на модифицированный происходит с вероятностью, напрямую зависящей от разницы коэффициентов основного и модифицированного ключей.
5. Шаги 2-4 повторяются около 50 000 раз.

Алгоритм периодически замещает основной ключ, ключом с худшими характеристиками. При этом вероятность замены зависит от разницы характеристик, что не позволяет алгоритму принимать плохие варианты слишком часто.

Для расчета коэффициентов, определяющих принадлежность текста к естественному языку лучше всего использовать частоты появления триграмм.

Шифр Виженера

Шифр Виженера относится к группе полиалфавитных шифров подстановки. Это значит, что в зависимости от ключа одна и та же буква открытого текста может быть зашифрована в разные символы. Такая техника шифрования скрывает все частотные характеристики текста и затрудняет криптоанализ.

Шифр Виженера представляет собой последовательность нескольких шифров Цезаря с различными ключами.

Продемонстрируем, в качестве примера, шифрование слова HABRAHABR с помощью ключа 123. Запишем ключ под исходным текстом, повторив его требуемое количество раз:

Цифры ключа определяют на сколько позиций необходимо сдвинуть букву в алфавите для получения шифртекста. Букву H необходимо сместить на одну позицию — в результате получается буква I, букву A на 2 позиции — буква C, и так далее. Осуществив все подстановки, получим в результате шифртекст: ICESCKBDU.

Криптоанализ шифра Виженера

Первая задача, стоящая при криптоанализе шифра Виженера заключается в нахождении длины, использованного при шифровании, ключа.

Для этого можно воспользоваться индексом совпадений.

Индекс совпадений — число, характеризующее вероятность того, что две произвольно выбранные из текста буквы окажутся одинаковы.
Для любого текста индекс совпадений вычисляется по формуле:

,

где f_i — количество появлений i-й буквы алфавита в тексте, а n — количество букв в тексте.

Для английского языка индекс совпадений имеет значение 0.0667, в то время как для случайного набора букв этот показатель равен 0.038.
Более того, для текста зашифрованного с помощью одноалфавитной подстановки, индекс совпадений также равен 0.0667. Это объясняется тем, что количество различных букв в тексте остается неизменным.

Это свойство используется для нахождения длины ключа шифра Виженера. Из шифртекста по очереди выбираются каждая вторая буквы и для полученного текста считается индекс совпадений. Если результат примерно соответствует индексу совпадений естественного языка, значит длина ключа равна двум. В противном случае из шифртекста выбирается каждая третья буква и опять считается индекс совпадений. Процесс повторяется пока высокое значение индекса совпадений не укажет на длину ключа.

Успешность метода объясняется тем, что если длина ключа угадана верно, то выбранные буквы образуют шифртекст, зашифрованный простым шифром Цезаря. И индекс совпадений должен быть приблизительно соответствовать индексу совпадений естественного языка.
После того как длина ключа будет найдена взлом сводится к вскрытию нескольких шифров Цезаря. Для этого можно использовать способ, описанный в первом разделе данного топика.

Исходники всех вышеописанных шифров и атак на них можно посмотреть на GitHub.

Источник