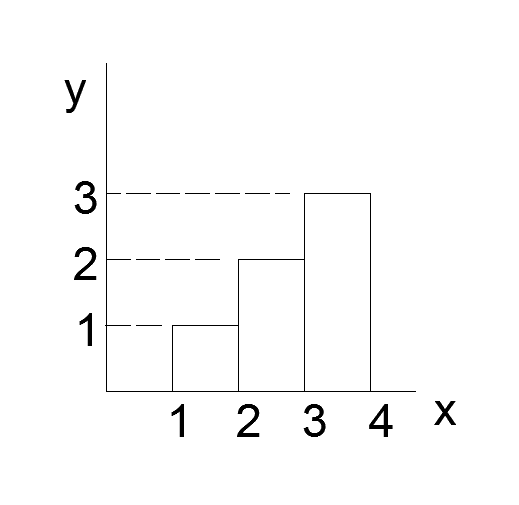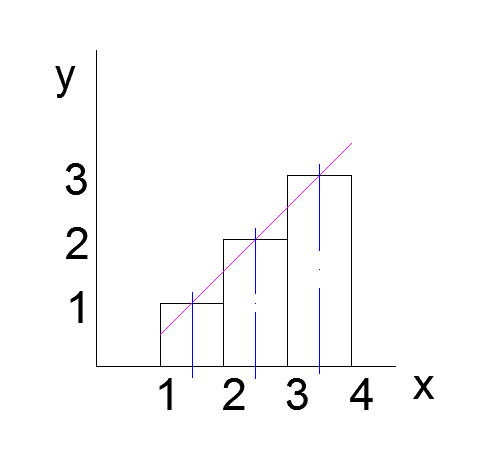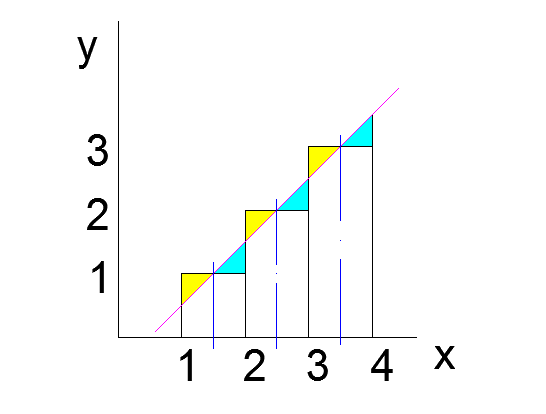Как сложить числа от 1 до 100 удобным способом

Сумма чисел от 1 до 100?

Всем привет! В предыдущей статье я предложил Вам задачу, которую юный Карл Гаусс решил очень быстро в десятилетнем возрасте. Вот она: найти сумму всех чисел от 1 до 100, не складывая их всех одно за другим по-порядку. Согласитесь, если все числа прибавлять одно к другому, это займёт очень много времени. Да и нет гарантии, что ты где-нибудь не ошибёшься в расчётах, особенно если делаешь это устно. На это и надеялся учитель математики, который дал это задание классу, в котором учился Гаусс. Преподаватель думал, пока его ученики увлечены решением, спокойно заняться своими делами. Но наш юный герой очень быстро нашёл решение для этой задачи. Так как же он это сделал?

Карл обратил внимание, что числа от 1 до 100 можно разбить на пары: 1 и 99, 2 и 98, 3 и 97, и т. д. Последняя пара — это 49 и 51. Таких пар получилось 49. Сумма каждой пары составляет 100. После разбивки на пары осталось два числа: 100 и 50. Теперь легко сосчитать: 49 пар по 100 — это 49х100=4900; плюс ещё 100 — это 5000; плюс 50 — это 5050.

Вот так, оказывается, всё просто, когда мыслишь нестандартно 🙂 Впоследствии Карл Гаусс стал известным математиком. В числе его великих трудов есть и тема арифметических прогрессий . Он нашёл формулы, по которым можно найти любой член прогрессии, зная его первый член и разность; а также сумму членов этой последовательности.

Про прогрессии я в последствии ещё обязательно Вам расскажу что-нибудь интересное. Это очень занимательная тема!

Спасибо, что прочитали статью! Надеюсь, Вам было интересно.

Буду благодарен за Ваши лайки, комментарии и подписки.

Источник

Блог питониста

Как сложить числа от 1 до 100 (перевод)

8 октября 2017 г.

Согласно распространенной истории, школьный учитель математики Гаусса был ленив. Чтобы чем-то занять детей на долгое время, а самому вздремнуть, он попросил их сложить числа от 1 до 100.

Гаусс быстро дал ответ: 5050. Так быстро? Учитель не поверил, но юный гений оказался прав. Складывать все числа от 1 до 100 — это для слабаков! Гаусс нашёл формулу:

Как это у него получилось? Давайте попробуем разобраться на примере суммы от 1 до 10.

Первый способ: разбить числа на пары

Запишем числа от 1 до 10 в виде матрицы c двумя строками и пятью столбцами:

Интересно, сумма каждого столбца равна 11 или $n+1$. И всего таких пар чисел 5 или $\frac<2>$. Получаем нашу формулу:

$$Число\ столбцов\cdotСумма\ чисел\ в\ стобцах=\frac<2>\cdot(n+1)$$

Если нечетное число слагаемых?

Что, если сложить числа от 1 до 9? У нас не хватает одного числа для составления пяти пар, но мы можем взять ноль:

Сумма столбцов теперь равна 9 или ровно $n$. А количество столбцов? По-прежнему пять столбцов (спасибо нулю!), но теперь количество столбцов определяется как $\frac<2>$ ( y нас $n+1$ чиcел и вдвое меньше столбцов).

$$Число\ столбцов\cdotСумма\ чисел\ в\ стобцах=\frac<2>\cdot n$$

Второй способ: увеличить вдвое и записать в две строки

Мы немного по-разному считаем сумму чисел в этих двух случаях.
Может быть, есть способ одинаково посчитать сумму для четного и нечетного количества слагаемых?

Вместо того, чтобы делать из чисел своеобразную «петлю», давайте запишем их в две строки, при этом количество чисел умножим на два:

Для нечетного случая:

Видно, что в обоих случаях сумма столбцов равна $n+1$, а количество столбцов $n$.

$$Число\ столбцов\cdotСумма\ чисел\ в\ стобцах=n\cdot(n+1)$$

Но нам нужна сумма только одной строки, поэтому:

Третий способ: сделать прямоугольник

Есть еще одно объяснение, давайте попробуем сложить крестики, допутим у нас есть крестики:

Как нам посчитать количество крестиков? Давайте добавим такое же количество ноликов:

Похоже просто на другое представление второго способа — каждая последующая строка пирамидки имеет больше крестиков и меньше ноликов. Количество всех крестиков и ноликов — площадь прямоугольника.

Но нам нужна сумма крестиков, поэтому:

Четветрый способ: среднее арифметическое

Известно: $Среднее\ арифметическое=\frac<Сумма><Количество\ членов>$
Тогда: $Сумма = среднее\ арифметическое\cdotКоличество\ членов$

Количество членов нам известно — $n$. А как выразить Cреднее арифметическое?

Заметьте, числа распределены равномерно. На каждое большое число приходится маленькое, расположенное на другом конце.

1 2 3, среднее 2

1 2 3 4, среднее 2.5

В этом случае среднее арифметическое — это среднее арфиметическое чисел 1 и $n$, тоесть $Среднее\ арифметическое=\frac<2>$

Пятый способ: интеграл

Все мы знаем, что определенный интеграл вычисляет сумму. Посчитаем сумму от 1 до 100 интегралом? Да, но для начала давайте хотя бы найдем сумму от 1 до 3. Пусть наши числа будут функцией y(x). Нарисуем картинку:

Высоты трех прямоугольников — как раз числа от 1 до 3. Проведем прямую через середины «шапок»:

Неплохо было бы найти уравнение этой прямой. Она проходит через точки (1.5;1) и (2.5;2). $y=k\cdot x+b$.

$$\begin2.5k + b = 2\\1.5k + b = 1\end\Rightarrow k=1; b=-0.5$$

Таким образом, уравнение прямой, которой мы можем аппроксимировать наши прямоугольники $y=x-0.5$

Она отсекает от прямоугольников желтые треугольники, но «добавляет» к ним сверху голубые. Желтые равны голубым. Сначала убедимся, что использование интеграла ведёт к формуле Гаусса:

Теперь посчитаем сумму от 1 до 3, по иксу берем от 1 до 4, чтобы все наши три прямоугольника попали в интеграл:

Чтобы посчитать сумму от 1 до 100 нужно взять интеграл от 1 до 101:

И зачем все это нужно?

Наша формула позволяет быстро подсчитать сумму чисел. Заметьте:

В первый день на ваш сайт зашел один человек, на второй день двое… Каждый день количество посещений увеличивалось на 1. Сколько всего посещений наберет сайт к концу 1000-го дня?

Данная статья — перевод с небольшим моим дополнением, оригинал.

Источник

Математика

Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет

С этой картой можно накопить на мечту, жми ⇒

План урока:

Мудрая Сова: Здравствуйте, дорогие ребята! Вы меня узнали? Конечно, это я, мудрая Сова!

Я рада приветствовать вас снова в нашей лесной школе. Мои верные друзья : черепашка Маша, кошка Алиса и енот Кузьма отлично отдохнули летом и готовы помогать вам изучать математику в третьем классе.

Вы все помните, что мы с вами изучали в прошлом году? Давайте проверим ваши знания.

В прошлом году наши уроки начинались с устного счета. Напомните, для чего он нужен? Правильно, для того, что разогреть наш мозг и подготовиться решать примеры и задачи.

Кузьма уже подготовил вам задания для устного счета.

1. Задание для устного счета

36 увеличьте на 8.

На сколько 18 больше 9?

Уменьшите 17 на 8.

19 меньше неизвестного числа на 12. Чему равно неизвестное число?

Найдите сумму чисел: 16 и 17.

Вычислите значение разности чисел: 24 и 16.

Сумма каких однозначных чисел равна 16?

Для детского сада купили 16 кукол, а мячей на 9 меньше. Сколько мячей купили для детского сада?

Сыну 22 года. Его отцу 50 лет. На сколько лет сын моложе отца?

Ответы в конце урока!

Повторяем состав чисел

Сова: Хорошо. Посмотрим, как ребята помнят состав чисел. Что такое состав чисел? Правильно. Это два числа, из которых состоит каждое число. А зачем нам нужно знать состав чисел? Чтобы быстро считать удобным способом.

Давайте вспомним, как мы это делали во втором классе. Например, нам нужно найти сумму чисел 23 и 50. Что мы с вами будем делать? Разложим число 27 на два слагаемых: 20 и 7. Теперь нам легче будет сложить десятки и к полученной сумме прибавить три единицы.

Вспомнили? Решите несколько примеров, используя свои знания о составе чисел.

Сова: Молодцы, ребята! О, черепашке Маше уже не терпится решать с вами задачи. Что ты ребятам сегодня приготовила?

Решаем задачи различными способами

Черепашка Маша: Мы сегодня с ребятами вспомним, как решать задачи разными способами.

Задание 2. Найдите из предложенных утверждений правильные:

Задачу можно решить по действиям с пояснениями или по вопросам.

Задачу можно решить, используя свой опыт. V

Задачу можно решить выражением.

Задачу можно решить арифметически. V

Задачу можно решить алгебраически . V

Задачу можно решить графически. V

Ответ в конце урока!

Вспомним, что значит решить задачу, используя свой опыт? Помните, в первом классе мы еще не знали сложение и вычитание, но используя палочки или другой счетный материал, мы решали задачи про птиц, которые прилетели или улетели, про морковки и зайцев, пересчитывая их. Это и есть наш опыт.

Познакомившись с понятием сложение и вычитание, мы стали записывать решение уже арифметически, с помощью примеров.

Задачи на умножение и деление мы решали с помощью чертежа или рисовали схему – это графический способ.

А уравнения мы решаем, каким способом? Правильно, алгебраическим, т.к. неизвестное число обозначали латинской буквой и находили его значение.

Вот вам три задачи, которые нужно решить, выбрав один из известных вам способов и указать его в ответе.

Задача 1. Почтальон разнес 47 писем. Ему осталось разнести еще 15. Сколько всего писем оно должен разнести?

47 + 15 = 62 (письма) – арифметический способ.

Задача 2. Красная шапочка сначала шла до автобусной остановки 10 минут, потом ехала на автобусе 39 минут, и затем, до бабушкиного дома её подвез Буратино. Всего в пути Красная шапочка была час. Сколько минут её катал на велосипеде Буратино?

Решили графическим способом.

Задача 3. В школьную библиотеку из второго класса записалось 46 школьников. Девочек, 24 , остальные мальчики. Сколько мальчиков записалось в школьную библиотеку?

Решили алгебраическим способом.

Сова: Ай да ребята! Ай да молодцы! Как ловко вы решаете задачи различными способами. Пришло время немного отдохнуть.

Определяем верные и неверные равенства

Сова : Продолжаем работать. Вспомним, что такое равенство и неравенство?

Равенство это когда левая часть выражения (примера) равна правой. Например, 12+4 = 16. В равенстве используют знак «=»

А неравенство – левая часть выражения больше или меньше правой. Например, 12+4

Повторили? А теперь, закрепим.

Задача 4. Вам нужно будет выписать только неверные неравенства.

(Правильные ответы выделены курсивом)

А кто у нас тут, рисует различные геометрические фигуры? Алиса!

Геометрические фигуры и задачи

Кошка Алиса: Мур, мур! Да, я люблю рисовать различные геометрические фигуры. А ребята помнят геометрические фигуры?

Задача 5. Назовите все геометрические фигуры, которые видите.

Сова: Ну что скажешь, Алиса, знают ребята геометрические фигуры?

Алиса: Мур, мур, знают. А вот, помнят они, как чертить отрезки, делить их и обозначать буквами?

Сова: А ты проверь. Дай им задачу и посмотри, помнят или забыли за лето?

Алиса: Хорошо. Вот вам геометрическая задача.

Задача 6. Начертите в тетради отрезок АВ длиной 1 дм 2 см. Разделите его точками на три равные части. Обозначьте буквами отмеченные точки. Запишите все полученные отрезки.

Ответ в конце урока!

Алиса: Великолепно! Мур, мур. Молодцы, ребята! Пойду придумывать вам новые геометрические задачи.

Логическая задача от мудрой Совы

Сова: Наш урок подходит к концу. Но у меня для вас есть задача на смекалку.

Задача 7. В записи 8 8 8 8 8 8 поставьте между некоторыми цифрами два знака действия и скобки так, чтобы полученное выражение имело значение

Правильный ответ в конце урока!

Ребята, давайте подведем итоги нашего сегодняшнего урока.

Сегодня мы повторили темы:

-решение задач различными способами;

-верные и неверные равенства;

И давайте сверим ответы:

Задание 1. 44, 9,9,31,33,8,8,7,28

Задание 2. (правильные ответы выделены V )

Первое и третье утверждение о формах записи задачи, а не способ их решения.

Задача 6. АС, СD, DB.

Задача 7.

1. (88-88) х 88 = 0 х 88 = 0

2. (888-88):8 = 800 : 8 = 100

Спасибо моим друзьям: Кузьме, Маше и Алисе за помощь в проведении урока.

Источник

Вычисли удобным способом значение суммы чисел от 1 до 10

Ответ или решение 2

В предложенном задании нас просят вычислить удобным способом сумму чисел от 1 до 10 включительно. Для простого решения данной и подобных заданий существует специальный способ.

Способ вычисления суммы чисел в промежутке

• Для решения подобного рода задач необходимо составить максимальное количество пар, которые в сумме дают одно и то же число, плюс само это число, которое, как правило, является последним в промежутке.
• Затем умножить количество этих пар плюс ещё один (само число) на число, которое они дают в сумме.
• Теперь осталось прибавить число из середины промежутка, которое осталось без пары. Так мы легко и максимально быстро получим правильный ответ.

Рассмотрим на примере промежутка от 1 до 100

• Составим максимальное количество пар, которые в сумме дают одно и тоже число. Такими парами будут 1 и 99, 2 и 98, 3 и 97, 4 и 96 и так далее до пары 49 и 51. В сумме они дают 100. Таких пар всего будет 49 (потому что на 49 мы остановились), плюс само число 100, на которое оканчивается промежуток, то есть получается 50 пар по сто.
• Умножаем количество пар, то есть 50 на саму их сумму, то есть также на 100:

• Теперь осталось только прибавить число 50, которое не имеет пару и поэтому не было посчитано:

• Всё, так мы нашли сумму всех цифр от 1 до 100 включительно.

Наконец, используя данный метод вычисления, можем выполнить предложенное задание.

Сумма цифр от 1 до 10

• В данном примере пары будут такими: 1 и 9, 2 и 8, 3 и 7, 4 и 6, которое дают в сумме 10, плюс само число 10.
• Теперь умножаем количество пар, то есть 5 на их сумму, то есть на 10:

• Осталось только прибавить число 5, которое не имело пары:

У данной задачи есть как минимум два решения. Первый самый простой, но не совсем удобный. Для этого просто нужно сложить весь цифрой ряд от 1 до 10 между собой.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55:

Но есть способ немного проще и быстрее. В ряду от от единицы до десяти находится 10 цифр, если разложить их двумя рядами, то и сложить, то можно увидеть закономерность.

То есть если числовой ряд кратен двум и не прерывается, то достаточно сложить сложить первую и последнюю цифру в числовом ряду и умножить ее на половину количества цифр в числовом ряду.

Источник