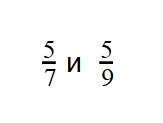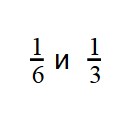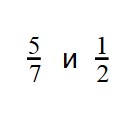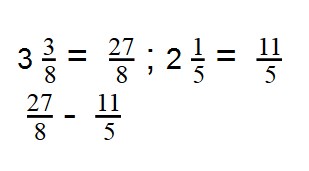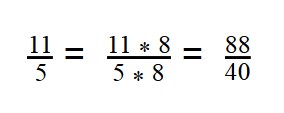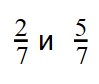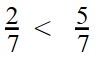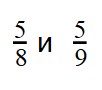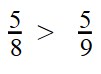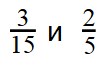Как самым простым способом не применяя никаких приборов определить больше или меньше

§ 5. Точность и погрешность измерений

Всякое измерение может быть выполнено с большей или меньшей точностью.

В качестве примера рассмотрим измерение длины ручки демонстрационным метром с сантиметровыми делениями (рис. 14).

Вначале определим цену деления линейки. Она будет равна 1 см.

Если верхний конец ручки совместить с нулевым штрихом, то нижний будет находиться между 11 и 12 штрихами, но ближе к 11.

Какое же из этих двух значений следует принять за длину ручки? Очевидно, то, которое ближе к истинному значению, т. е. 11 см.

Считая, что длина ручки 11 см, мы допустили неточность, так как ручка чуть длиннее 11 см.

В физике допускаемую при измерении неточность называют погрешностью измерений.

Погрешность измерения не может быть больше цены деления шкалы измерительного прибора.

В нашем случае погрешность измерения ручки не превышает 1 см. Если такая точность измерений нас не удовлетворяет, то можно произвести измерения с большей точностью. Но тогда придётся взять масштабную линейку с миллиметровыми делениями, т. е. с ценой деления 1 мм.

В этом случае длина ручки окажется равной 11,2 см.

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.

Чем меньше цена деления, тем больше точность измерения.

Точность измерения зависит также от правильного применения измерительного прибора, расположения глаза при отсчёте по прибору.

Вследствие несовершенства измерительных приборов и наших органов чувств при любом измерении получаются лишь приближённые значения, несколько большие или меньшие истинного значения измеряемой величины.

Во время выполнения лабораторных работ или просто измерений следует считать, что погрешность измерений равна половине цены деления шкалы измерительного прибора.

Измерим длину карандаша. Нулевую отметку линейки совместим с одним концом карандаша, а другой её конец окажется вблизи 14 см. Цена деления линейки 1 мм, тогда погрешность измерения будет равна 0,5 мм или 0,05 см.

Следовательно, длину карандаша можно записать в виде

где I — длина карандаша.

Истинное значение длины карандаша находится в интервале от 13,95 см до 14,05 см.

При записи величин, с учётом погрешности, следует пользоваться формулой

где А — измеряемая величина, а — результат измерений, Δа — погрешность измерений (Δ — греч. буква «дельта»).

Вопросы

1. Как понимать выражение «измерить длину с точностью до 1 мм»?
2. Можно ли линейкой, имеющей сантиметровые деления, измерить длину с точностью до 1 мм?
3. Какова связь точности измерений с ценой деления шкалы прибора?
4. Какой формулой необходимо пользоваться при записи физических величин с учётом погрешности?

Задание

1. Измерьте линейкой с миллиметровыми делениями длину и ширину вашего учебника. Запишите результаты с учётом погрешности измерения.

2. Пользуясь рисунком 11, б, определите погрешность измерения термометра.

3. Измерьте линейкой с миллиметровыми делениями длину и высоту картины Л. да Винчи (рис. 15). Запишите результаты измерений с учётом погрешности. Используя Интернет, найдите название картины, её истинный размер и определите масштаб, в котором картина представлена в учебнике.

Источник

Сравнение дробей, как правильно

О чем эта статья:

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

• Мы видим, что знаменатели дробей — равны. Значит сравниваем числители:
  8 8
• Это значит, что 10
  1

Пример 3. Сравните дроби:

• Знаменатели дробей снова равны. Сравниваем числители:
  3 > 1
  1

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.

Давайте разберем наглядный пример сравнения дробей:

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.

• Запишем в виде дробей: и
• А теперь сравним полученные дроби: знаменатели — равны, сравниваем числители:
  6 > 5
  5

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

• У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
  9 > 7
  7 10
• Значит дробь с меньшим знаменателем — больше:
  

Пример 3. Сравните дроби:

У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
6 > 3
3

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

• Нужно подобрать число, которое будет делиться на 7 и на 2 (найти наименьшее общее кратное НОК). В данном случае, НОК — 14. Проверим:
  14:7 = 2
  14 : 2 = 7
• Первую дробь умножаем на дополнительный множитель 2:
  
• Вторую дробь умножаем на дополнительный множитель 7:
  
• Дроби приведены к общему знаменателю:
  

Давайте потренируемся в сравнении дробей.

Пример 1. Сравните дроби:

• Приведем дроби к общему знаменателю. 30 делится на 15 и на 2.
  30 : 15 = 2
  30 : 2 = 15
• Первую дробь умножаем на дополнительный множитель 2:
  
• Вторую дробь умножаем на дополнительный множитель 15:
  
• Дроби приведены к общему знаменателю:
  
• Если две дроби имеют одинаковые знаменатели, то, согласно правилу, больше та дробь, чей числитель больше:
  

При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

• 6/5 — неправильная дробь.
• Выделим целую часть:
• Значит, что

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.

• 12 — 7 = 6
  12 — уменьшаемое
  7 — вычитаемое
  5 — разность

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.

Пример 1. Найдите разность:

• 

Вычитаемая дробь меньше уменьшаемой

• Выполняем вычитание:

Пример 2.Найдите разность:

• Смешанные дроби превращаем в неправильные:
  
• Чтобы сравнить дроби с разными числителями и знаменателями, нужно привести их к общему знаменателю:
  
• Наименьшее общее кратное — 40
  40 : 8 = 5
  40 : 5 = 8
• Умножаем первую дробь на дополнительный множитель 5:
  
• Умножаем вторую дробь на дополнительный множитель 8:
  
• Дроби приведены к общему знаменателю:
  

Если знаменатели одинаковые — больше та дробь, числитель которой больше.

• Мы видим, что вычитаемое меньше уменьшаемого, значит можем без труда найти разность:
  

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

Пример 2. Сравните дроби:

Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

Пример 3. Сравните дроби:

Ответ:.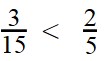

• По правилу сравнения дробей с разными числителями и знаменателями, сначала нужно привести дроби к общему знаменателю:
  
• Наименьшее общее кратное — 15:
  15 : 15 = 1
  15 : 5 = 3
• Умножаем первую дробь на дополнительный множитель 1:
  
• Умножаем вторую дробь на дополнительный множитель 3:
  
• Дроби приведены к общему знаменателю:
  
• Сравниваем числители получившихся дробей: 3

Источник