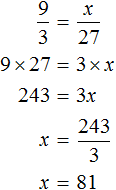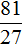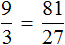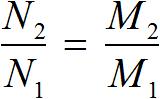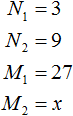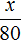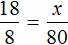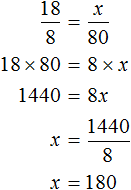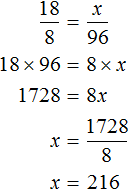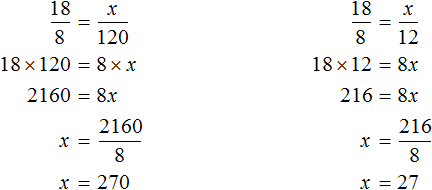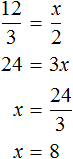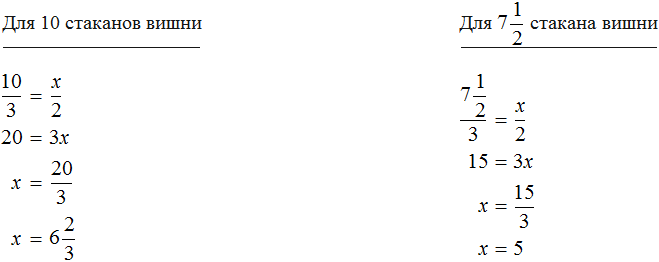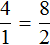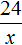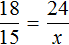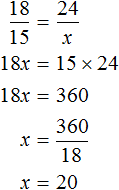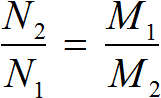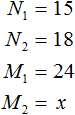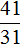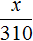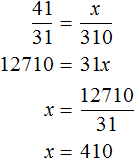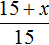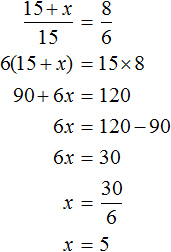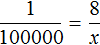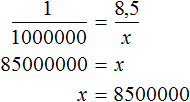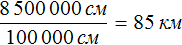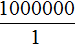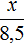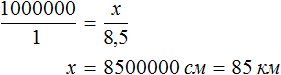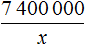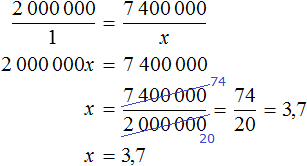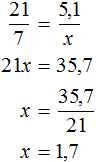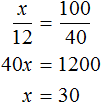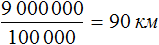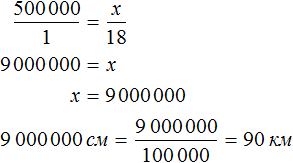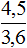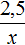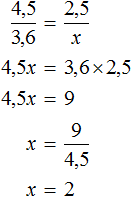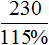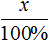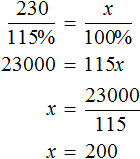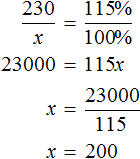- Задачи на пропорции
- Решение задач на пропорции
- Задача
- Прямая и обратная пропорциональность
- Основные определения
- Прямо пропорциональные величины
- Обратно пропорциональные величины
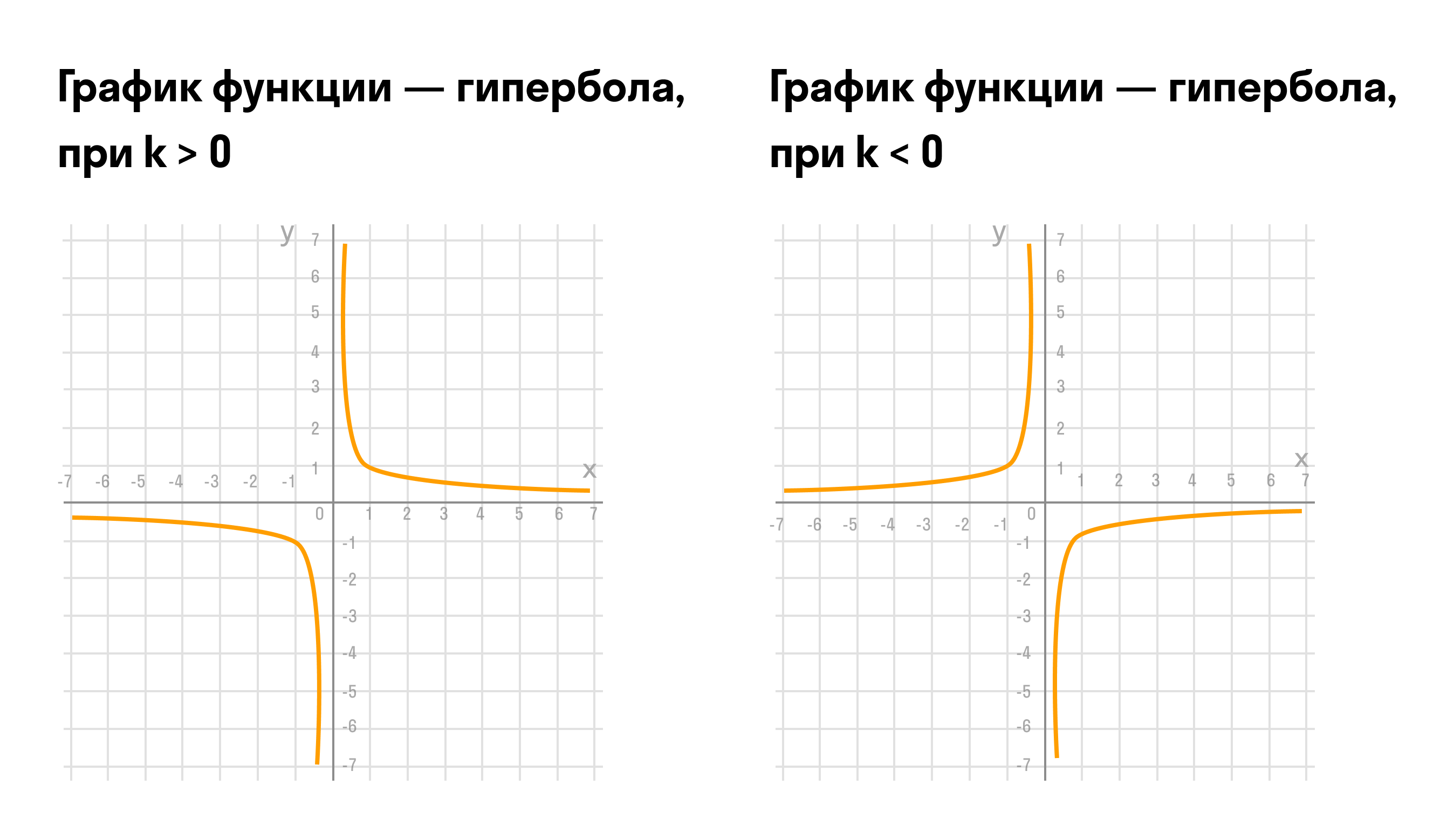
- Свойства функции обратной пропорциональности:
- Потренируемся
- Решение задач с помощью пропорции
- Как решить задачу с помощью пропорции
- Отношение одноименных величин
- Задачи на прямую пропорциональность
- Задачи на обратную пропорциональность
- Масштаб
- Задачи для самостоятельного решения
- 11 thoughts on “Решение задач с помощью пропорции”
Задачи на пропорции
По трём известным членам пропорции всегда можно найти её неизвестный (четвёртый) член.
Решить пропорцию — значит, найти все её члены. Решим пропорцию ниже
(найдём « x »).
Чтобы найти « x », используем основное свойство пропорции (правило «креста»).
Теперь мы готовы разбираться, как решать задачи на пропорции.
Решение задач на пропорции
Часто задачи на пропорции тесно связаны с процентами. Свои знания о процентах, вы можете освежить в разделе «Проценты».
Задача
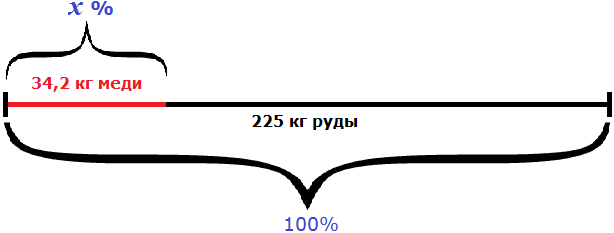
Из лука сделано 50 выстрелов. 5 стрел пролетело мимо мишени. Определите процент попадания .
По традиции подчёркнем важные и числовые данные в задаче.
Обратите внимание, что нам нужно определить процент попаданий, а не процент пролетевших мимо стрел.
Поэтому вначале посчитаем, сколько стрел попало в цель. Сделать это не составит труда.
- 50 − 5 = 45 (стрел) — попало в цель.
Далее для решения задачи составим таблицу, куда занесём все данные. Запомните, что напротив 100% в таблице обычно пишется общее количество чего-либо. Неизвестные проценты обозначим буквой x .
| Стрелы | Проценты | |
|---|---|---|
| Всего выпущено | 50 | 100 % |
| Попало в цель | 45 | x % |
Чтобы правильно записывать нужные данные в таблицу, запомните простое правило.
Одинаковые наименования нужно записывать друг под другом. Проценты записываем под процентами, килограммы под килограммами и т.д.
Теперь, используя таблицу, составим нужную пропорцию и решим её с помощью правила «креста».
Источник
Прямая и обратная пропорциональность
О чем эта статья:
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
- Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.
- Обратная зависимость. Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.
Зависимости также можно классифицировать по формам: функциональная и статистическая.
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.
В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.
Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.
Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
- Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз. А уменьшение одно числа ведет к уменьшению другого во столько же раз.
- Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз. А увеличение числа наоборот ведет к уменьшению другого во столько же раз.
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
- при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
- периметр квадрата и его сторона — прямо-пропорциональные величины;
- стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график выглядит так:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
- Вспомним формулу для определения пути через скорость и время: S = V * t.
- Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений: 70 * 2 = V * 7
- Найдем скорость второго автомобиля: V = 70 * 2/7 = 20
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
- х = 1 (блогер) * 30 (раз) : 12/8 (дней).
- х = 1 * 30 : 12/8
- х = 20
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
- время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;
- при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;
- количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.
| Где | 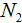 − новое значение первой величины − новое значение первой величины |
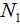 − старое значение первой величины − старое значение первой величины | |
| − новое значение второй величины | |
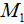 − старое значение второй величины − старое значение второй величины |
Применительно к нашей задаче значения переменных 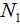
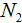
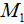
Где впоследствии стало равно 81.
Задача 2. Для 8 коров в зимнее время доярка ежедневно заготовляет 80 кг сена, 96 кг корнеплодов, 120 кг силоса и 12 кг концентратов. Определить ежедневный расход этих кормов для 18 коров.
Решение
Количество коров и масса каждого из кормов — прямо пропорциональные величины. При увеличении количества коров в несколько раз, масса каждого из кормов увеличится во столько же раз.
Составим несколько пропорций, вычисляющих массу каждого из кормов для 18 коров.
Начнем с сена. Ежедневно для 8 коров его заготовляют 80 кг. Тогда для 18 коров будет заготовлено x кг сена.
Запишем отношение, показывающее во сколько раз увеличилось количество коров:
Теперь запишем отношение, показывающее во сколько раз увеличилась масса сена:
Соединим эти отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит для 18 коров нужно заготовить 180 кг сена. Аналогично определяем массу корнеплодов, силоса и концентратов.
Для 8 коров ежедневно заготовляют 96 кг корнеплодов. Тогда для 18 коров будет заготовлено x кг корнеплодов. Составим пропорцию из отношений 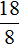
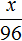
Определим сколько силоса и концентратов нужно заготовить для 18 коров:
Значит для 18 коров ежедневно нужно заготавливать 180 кг сена, 216 кг корнеплодов, 270 кг силоса и 27 кг концентратов.
Задача 3. Хозяйка варит вишнёвое варенье, причём на 3 стакана вишни кладёт 2 стакана сахара. Сколько сахара нужно положить на 12 стаканов вишни? на 10 стаканов вишни? на 
Решение
Количество стаканов вишни и количество стаканов сахарного песка — прямо пропорциональные величины. При увеличении количества стаканов вишни в несколько раз, количество стаканов сахара увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество стаканов вишни:
Теперь запишем отношение, показывающее во сколько раз увеличилось количество стаканов сахара:
Соединим эти отношения знаком равенства, получим пропорцию и найдем значение x
Значит на 12 стаканов вишни нужно положить 8 стаканов сахара.
Определим количество стаканов сахара для 10 стаканов вишни и 
Задачи на обратную пропорциональность
Для решения задач на обратную пропорциональность опять же можно использовать пропорцию, составленную из отношений одноименных величин.
В отличие от прямой пропорциональности, где величины увеличиваются или уменьшаются в одну и ту же сторону, в обратной пропорциональности величины изменяются обратно друг другу.
Если одна величина увеличивается в несколько раз, то другая уменьшается во столько же раз. И наоборот, если одна величина уменьшается в несколько раз, то другая увеличивается во столько же раз.
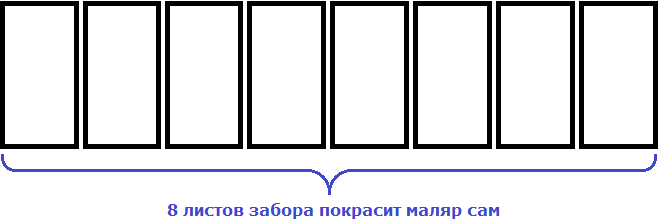
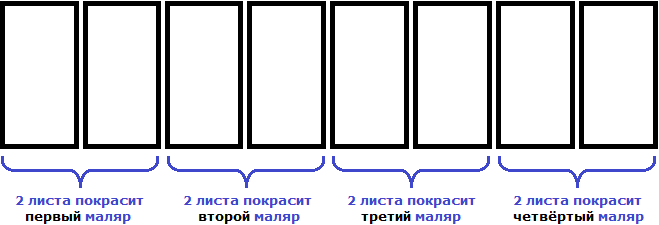
Допустим, что нужно покрасить забор, состоящий из 8 листов
Один маляр будет красить все 8 листов сам
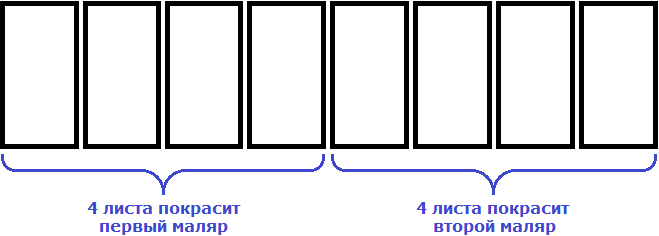
Если маляров будет 2, то каждый покрасит по 4 листа.
Это конечно же при условии, что маляры будут честными между собой и справедливо разделят эту работу поровну на двоих.
Если маляров будет 4, то каждый покрасит по 2 листа
Замечаем, что при увеличении количества маляров в несколько раз, количество листов которые приходятся на одного маляра уменьшаются во столько же раз.
Итак, мы увеличили количество маляров с 1 до 4. Другими словами, увеличили количество маляров в четыре раза. Запишем это с помощью отношения:
В результате количество листов забора, которые приходятся на одного маляра уменьшилось в четыре раза. Запишем это с помощью отношения:
Соединим эти отношения знаком равенства, получим пропорцию
«4 маляра так относятся к 1 маляру, как 8 листов относятся к 2 листам»
Задача 2. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?
Решение
Количество рабочих и количество дней, затраченных на работу — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней, необходимых для выполнения этой работы, уменьшится во столько же раз.
Запишем отношение 18 рабочих к 15 рабочим. Это отношение будет показывать во сколько раз увеличилось количество рабочих
Теперь запишем второе отношение, показывающее во сколько раз уменьшилось количество дней. Поскольку количество дней уменьшится с 24 дней до x дней, то второе отношение будет отношением старого количества дней (24 дня) к новому количеству дней (x дней)
Соединим полученные отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит 18 рабочих выполнят необходимую работу за 20 дней.
Вообще, если взять две обратно пропорциональные величины и увеличить одну из них в определенное число раз, то другая уменьшится во столько же раз. Тогда отношение нового значения к старому значению первой величины будет равно отношению старого значения к новому значению второй величины.
Так и в предыдущей задаче старые значения были 15 рабочих и 24 дня. Количество рабочих было увеличено с 15 до 18 (т.е. было увеличено в 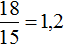
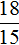
Для составления пропорции к задачам на обратную пропорциональность можно пользоваться формулой:
| Где | 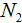 − новое значение первой величины − новое значение первой величины |
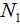 − старое значение первой величины − старое значение первой величины | |
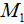 − старое значение второй величины − старое значение второй величины | |
| − новое значение второй величины |
Применительно к нашей задаче значения переменных 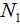
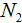
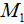
Где впоследствии стало равно 20.
Задача 2. Скорость парохода относится к скорости течения реки, как 36 : 5. Пароход двигался вниз по течению 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?
Решение
Собственная скорость парохода составляет 36 км/ч. Скорость течения реки реки 5 км/ч. Поскольку пароход двигался по течению руки, то скорость его движения составила 36 + 5 = 41 км/ч. Время пути составила 5 ч 10 мин. Для удобства выразим время в минутах:
5 ч 10 мин = 300 мин + 10 мин = 310 мин
Поскольку на обратном пути пароход двигался против течения реки, то его скорость составила 36 − 5 = 31 км/ч.
Скорость парохода и время его движения — обратно пропорциональные величины. При уменьшении скорости в несколько раз, время его движения увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз уменьшилась скорость движения:
Теперь запишем второе отношение, показывающее во сколько раз увеличилось время движения. Поскольку новое время x будет больше старого времени, в числителе отношения запишем время x , а в знаменателе старое время, равное трёхсот десяти минутам
Соединим полученные отношения знаком равенства, получим пропорцию 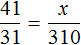
410 минут это 6 часов и 50 минут. Значит пароходу потребуется 6 часов и 50 минут, чтобы вернуться обратно.
Задача 3. На ремонте дороги работало 15 человек, и они должны были закончить работу за 12 дней. На пятый день утром подошли еще несколько рабочих, и оставшаяся работа была выполнена за 6 дней. Сколько рабочих прибыло дополнительно?
Решение
Вычтем из 12 дней 4 отработанных дня. Так мы определим сколько ещё дней осталось работать пятнадцати рабочим
12 дней − 4 дня = 8 дней
На пятый день дополнительно прибыло x рабочих. Тогда всего рабочих стало 15 + x .
Количество рабочих и количество дней, необходимых для выполнения работы — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней уменьшится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество рабочих:
Теперь запишем во сколько раз уменьшилось количество дней, необходимых для выполнения работы:
Соединим эти отношения знаком равенства, получим пропорцию 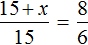
Значит 5 рабочих прибыло дополнительно.
Масштаб
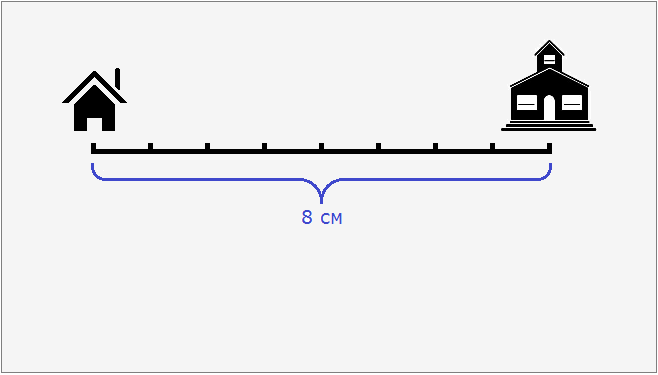
Масштабом называют отношение длины отрезка на изображении к длине соответствующего отрезка на местности.
Допустим, что расстояние от дома до школы составляет 8 км. Попробуем нарисовать план местности, где будут указаны дом, школа и расстояние между ними. Но изобразить на бумаге расстояние, равное 8 км мы не можем, поскольку оно довольно велико. Но зато мы можем уменьшить это расстояние в несколько раз так, чтобы оно уместилось на бумаге.
Пусть километры на местности на нашем плане будут выражаться в сантиметрах. Переведем 8 километров в сантиметры, получим 800 000 сантиметров.
Уменьшим 800 000 см в сто тысяч раз:
800 000 см : 100 000 см = 8 см
8 см это расстояние от дома до школы, уменьшенное в сто тысяч раз. Теперь без труда можно нарисовать на бумаге дом и школу, расстояние между которыми будет 8 см.
Эти 8 см относятся к реальным 800 000 см. Так и запишем с помощью отношения:
Одно из свойств отношения гласит, что отношение не меняется если его члены умножить или разделить на одно и то же число.
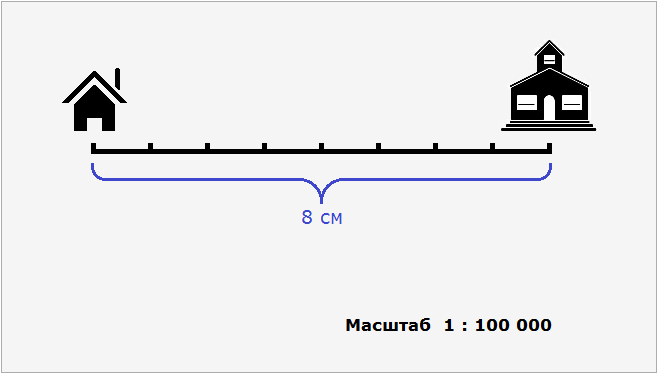
В целях упрощения отношения 8 : 800 000 оба его члена можно разделить на 8. Тогда получим отношение 1 : 100 000. Это отношение и назовём масштабом. Данное отношение показывает, что один сантиметр на плане относится (или соответствует) ста тысячам сантиметров на местности.
Поэтому на нашем рисунке необходимо указать, что план составлен в масштабе 1 : 100 000
1 см на плане относится к 100 000 см на местности;
2 см на плане относится к 200000 см на местности;
3 см на плане относится к 300000 на местности и т.д.
К любой карте или плану указывается в каком масштабе они сделаны. Этот масштаб позволяет определять реальное расстояние между объектами.
Так, наш план составлен в масштабе 1 : 100 000. На этом плане расстояние между домом и школой составляет 8 см. Чтобы вычислить реальное расстояние между домом и школой, нужно 8 см увеличить в 100 000 раз. Иными словами, умножить 8 см на 100 000
8 см × 100 000 = 800 000 см
Получаем 800 000 см или 8 км, если перевести сантиметры в километры.
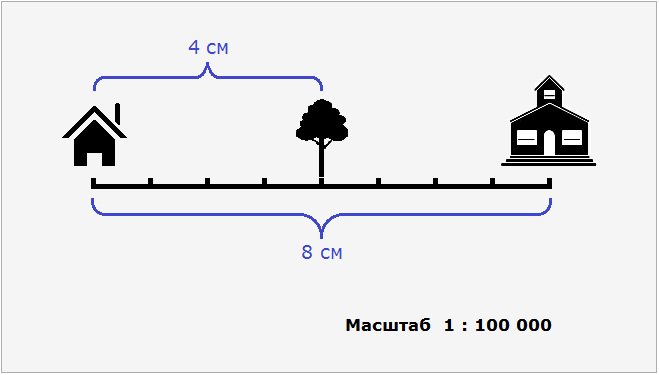
Допустим, что между домом и школой располагается дерево. На плане расстояние между школой и этим деревом составляет 4 см.
Тогда реальное расстояние между домом и деревом будет 4 см × 100 000 = 400 000 см или 4 км.
Расстояние на местности можно определять с помощью пропорции. В нашем примере расстояние между домом и школой будет вычисляться с помощью следующей пропорции:
Эту пропорцию можно прочитать так:
1 см на плане так относится к 100000 см на местности, как 8 см на плане относятся к x см на местности.
Из этой пропорции узнаём, что значение x равно 800000 см.
Пример 2. На карте расстояние между двумя городами составляет 8,5 см. Определить реальное расстояние между городами, если карта составлена в масштабе 1 : 1 000 000.
Решение
Масштаб 1 : 1 000 000 указывает, что 1 см на карте соответствует 1 000 000 см на местности. Тогда 8,5 см будут соответствовать x см на местности. Составим пропорцию 1 к 1000000 как 8,5 к x
В 1 км содержится 100000 см. Тогда в 8 500 000 см будет
Либо можно рассуждать так. Расстояние на карте и расстояние на местности — прямо пропорциональные величины. При увеличении расстояния на карте в несколько раз, расстояние на местности увеличится во столько же раз. Тогда пропорция примет следующий вид. Первое отношение будет показывать во сколько раз расстояние на местности больше расстояния на карте:
Второе отношение покажет, что расстояние на местности во столько же раз больше, чем 8,5 см на карте:
Отсюда x равен 8 500 000 см или 85 км.
Задача 3. Длина реки Невы 74 км. Чему равняется ее длина на карте, масштаб которой 1 : 2 000 000
Решение
Масштаб 1 : 2000000 говорит о том, что 1 см на карте соответствует 2 000 000 см на местности.
А 74 км на это 74 × 100 000 = 7 400 000 см на местности. Уменьшив 7 400 000 в 2 000 000, мы определим длину реки Невы на карте
7 400 000 : 2 000 000 = 3,7 см
Значит на карте, масштаб которой 1 : 2 000 000 длина реки Невы составляет 3,7 см.
Запишем решение с помощью пропорции. Первое отношение будет показывать сколько раз длина на карте меньше длины на местности:
Второе отношение будет показывать, что 74 км (7 400 000 см) уменьшились во столько же раз:
Отсюда находим x равный 3,7 см
Задачи для самостоятельного решения
Решение
Пусть x кг масла можно получить из 7 кг хлопкового семени. Масса хлопкового семени и масса получаемого масла — прямо пропорциональные величины. Тогда уменьшение хлопкового семени с 21 кг до 7 кг, приведет к уменьшению получаемого масла во столько же раз.
Ответ: из 7 кг хлопкового семени получится 1,7 кг масла.
Решение
Длина участка на котором производится замена рельсов равна 8 × 360 = 2880 м.
Пусть x двенадцатиметровых рельсов требуется для замены. Увеличение длины одного рельса с 8 м до 12 м приведет к уменьшению количества рельсов с 360 до x штук. Иными словами, длина рельса и их количество связаны обратно пропорциональной зависимостью
Ответ: для замены старых рельсов потребуется 240 новых.
Решение
Если 60% учащихся пошли в кино, а остальные 12 человек на выставку, то на 40% учащихся и будут приходиться 12 человек, пошедших на выставку. Тогда можно составить пропорцию в которой 12 учащихся так относятся к 40%, как все x учащихся относятся к 100%
Либо можно составить пропорцию, состоящей из отношений одноименных величин. Количество учащихся и процентная доля изменяются прямо пропорционально. Тогда можно записать, что во сколько раз увеличилось количество участников 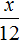
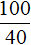
Ответ: в классе 30 учащихся.
Решение
Масштаб 1 : 500000 говорит о том, что 1 см на карте соответствует 500 000 см на местности.
Тогда увеличив 18 см в 500 000, мы получим действительное расстояние между городами
18 см × 500 000 = 9 000 000 см
Переведем 9 000 000 см в километры. В одном километре 100 000 см. Тогда в 9 000 000 см будет
Запишем решение с помощью пропорции:
Ответ: расстояние между городами 90 км.
Решение
Скорость и время — обратно пропорциональные величины. При увеличении скорости в несколько раз, время движения уменьшится во столько же раз.
Запишем отношение, показывающее по сколько раз увеличилась скорость движения пешехода:
Запишем отношение, показывающее что время движения уменьшилось во столько же раз:
Соединим эти отношения знаком равенства, получим пропорцию и найдём значение x
Ответ: пешеход затратит 2 часа если будет двигаться со скорость 4,5 км/ч.
Решение
Выражение «перевыполнили план на 15%» означает, что к имеющемуся 100% плану выполнили еще 15% того же плана. Итого выполнено 115% плана. На эти 115% приходятся 230 выпущенных станков
А по плану завод должен был выпустить x станков. Эти x станков приходятся на 100% изначального плана
Составим пропорцию из имеющихся отношений и найдём значение x
Либо можно воспользоваться отношениями одноименных величин. Количество выпущенных станков и процентная доля, на которые эти станки приходятся, связаны прямо пропорциональной зависимостью. При увеличении количества станков в несколько раз, процентная доля увеличивается во столько же раз. Тогда можно записать, что 230 станков во столько раз больше, чем x станков, во сколько раз больше 115%, чем 100%
Ответ: по плану завод должен был выпустить 200 станков.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
11 thoughts on “Решение задач с помощью пропорции”
Огромное спасибо за урок! Мне мама пыталась объяснить пропорции, а я не понимала) А теперь все просто благодаря вам!
Боже мой, почему мне так сложно? 🙁
Сразу не получится. Нужно время
Отличный урок! Пожалуйста, не забрасывайте этот проект, популяризировать математику необходимо. Уверен, многие люди, как и я, готовы поддержать Вас рублём, если вы дадите такую возможность. Большое спасибо за уже проделанную Вами работу, людей необходимо просвещать, особенно в наше время.
В разделе « решение задач с помощью пропорции» в задаче 2 есть фраза «сто километров так относятся к одному часу, как триста километров к неизвестному числу часов»:» и составлена пропорция 100/2= 300/x. Во
фразе опечатка, 100 километров при составлении пропорции относится к 2 часам а не к одному.
«составленнаю из отношений одноименных величин.» -> составленную
Источник





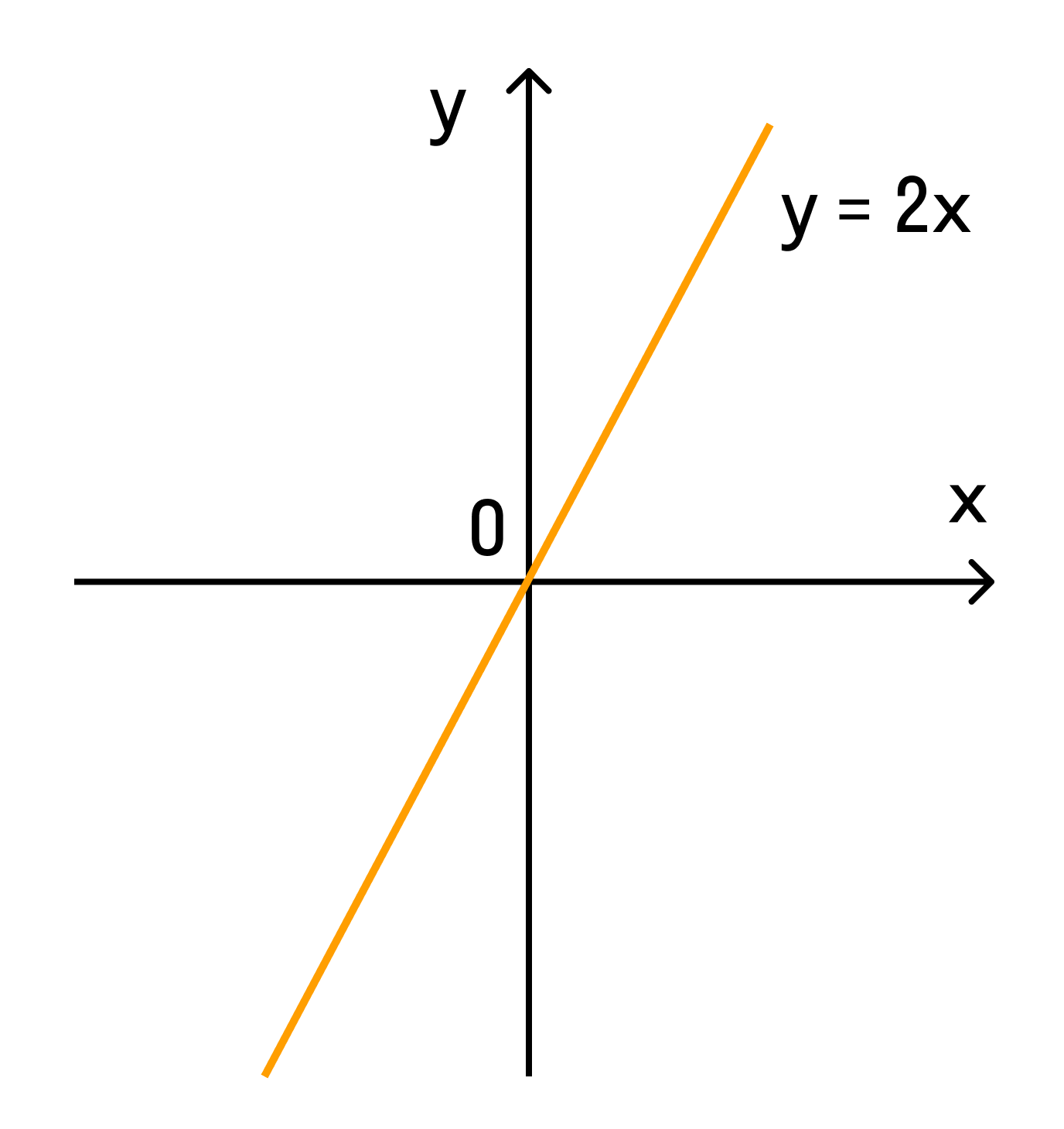


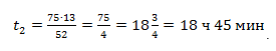
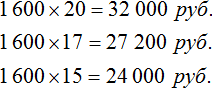
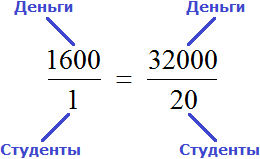
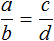 является пропорцией. Эту пропорцию можно прочесть следующим образом:
является пропорцией. Эту пропорцию можно прочесть следующим образом: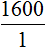
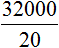
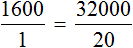
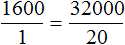 , то обнаружим, что одному студенту, как и двадцати студентам достанется по 1600 рублей.
, то обнаружим, что одному студенту, как и двадцати студентам достанется по 1600 рублей.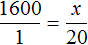 . То есть сумма денег, необходимая для выплаты стипендии, стала неизвестным членом пропорции. Эту пропорцию можно прочесть так:
. То есть сумма денег, необходимая для выплаты стипендии, стала неизвестным членом пропорции. Эту пропорцию можно прочесть так: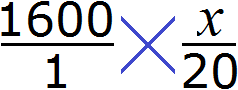
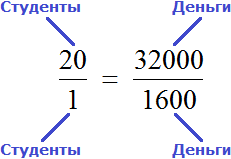
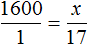 и
и 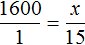 . Воспользовавшись основным свойством пропорции, можно найти значение x
. Воспользовавшись основным свойством пропорции, можно найти значение x 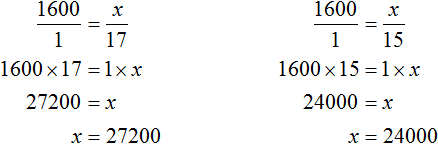
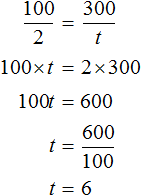
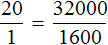 .
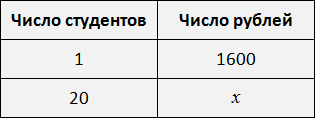
.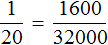 . Взаимосвязь при этом не нарушается. Отношение между студентами равно отношению между суммами денег, предназначенных для этих студентов. Такую пропорцию часто составляют в школе, когда для решения задачи составляются таблицы
. Взаимосвязь при этом не нарушается. Отношение между студентами равно отношению между суммами денег, предназначенных для этих студентов. Такую пропорцию часто составляют в школе, когда для решения задачи составляются таблицы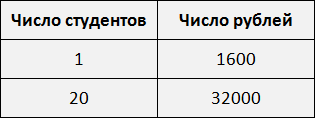
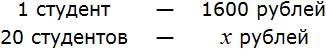
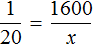
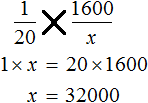

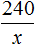
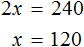
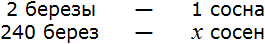
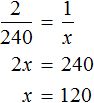
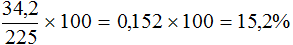
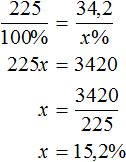

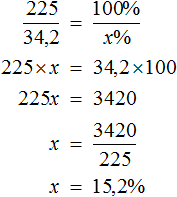

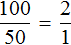

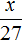
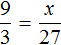 .
.