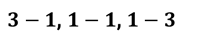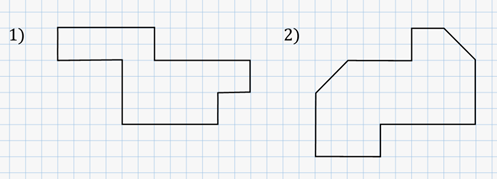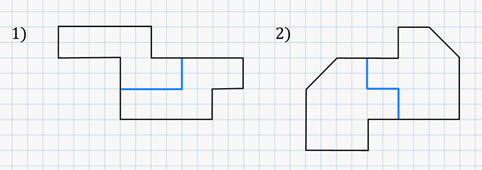Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки 
Средняя линия трапеции равна полусумме её оснований:
2. Найдите величину угла ABC. Ответ дайте в градусах.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:
Осталось умножить найденное значение синуса на
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 
Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 
Площадь трапеции равна произведению полусуммы оснований на высоту:
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:
Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 — 4 = 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.
На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.
Значит, нам надо умножить площадь круга на . Получим:
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.
Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
14. Найдите площадь четырехугольника, вершины которого имеют координаты
На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
Источник
Задачи на клетчатой бумаге
Урок 24. Математика и игры 3–4 классы
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Задачи на клетчатой бумаге»
Скорее всего, многие из вас задумывались, почему тетрадь по математике – в клеточку. Наверное, чтобы удобнее было записывать в столбик числа, чтобы легче было чертить. Также клеточки на бумаге позволяют нарисовать, или, как принято говорить, построить различные геометрические фигуры только с помощью обычной линейки и карандаша. При этом на линейке может даже не быть делений.
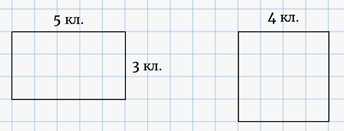
Построим прямоугольник. Его длина равна 5 клеточкам, а ширина – 3 клеточкам.
Можно построить квадрат. Например такой, сторона которого будет равна 4 клеточкам. А ведь мы знаем, что у квадрата все стороны равны.
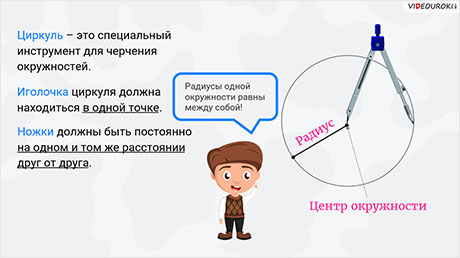
Бывают случаи, когда нам надо нарисовать окружность. Для этого мы можем воспользоваться циркулем.
Напомним, что циркуль – это специальный инструмент для черчения окружностей. Чтобы окружность получилась ровной и правильной, иголочка циркуля должна находиться в одной точке, и ножки должны быть постоянно на одном и том же расстоянии друг от друга.
Точка от иголочки – это центр окружности. Отрезок, который соединяет центр окружности с любой точкой, лежащей на этой окружности, называется радиусом.
Радиусы одной окружности равны между собой.
Но иногда бывают случаи, когда надо нарисовать окружность, а циркуля нет. Можно, конечно, попробовать нарисовать окружность от руки. Скорее всего, получится какой-то овал, отдалённо напоминающий окружность. Или просто замкнутая кривая. Конечно вы можете потренироваться это делать.
Так, великий немецкий художник Альбрехт Дюрер одним движением руки мог настолько точно нарисовать окружность, что даже проверка при помощи циркуля не показывала никаких отклонений.
Если же большая точность не требуется, и у вас есть бумага в клетку, то можно воспользоваться вот таким правилом…
Сразу отметим, что окружность, построенная по этому правилу, получается определённого размера.
Итак, начнём построение.
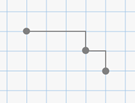
На пересечении линий клетчатой бумаги поставим точку. Посмотрите на правило. Первая его часть – «3 – 1». Это означает, что от точки отступим 3 клетки вправо и 1 клетку вниз. Поставим другую точку.
Смотрим дальше – «1 – 1». Отступим от второй точки по 1 клетке вправо и вниз, поставим третью точку.
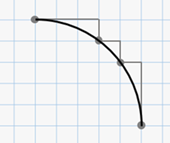
А следующий фрагмент записи – «3 – 1». Отступим 1 клетку вправо и 3 клетки вниз, поставим четвёртую точку. Теперь, соединив плавной линией полученные точки, мы получим одну четвёртую часть окружности.
Оставшуюся часть окружности можно дорисовать по такому же правилу. Только порядок действий изменится в противоположном направлении.
Итак, отступим на 3 клетки вниз и на 1 клетку влево. Поставим точку.
Затем отступим по 1 клетке вниз и влево. Поставим точку.
Далее, отступив 1 клетку вниз и 3 клетки влево, поставим ещё одну точку
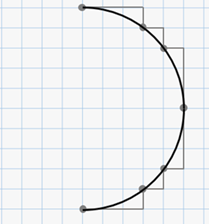
Соединим плавной линией полученные точки. Теперь получилась половина окружности.
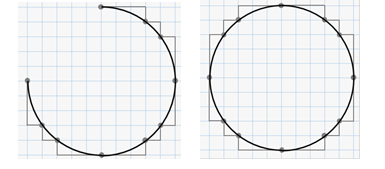
По такому же правилу можно дорисовать третью четверть окружности. Только теперь движение будет не вниз, а вверх. И четвёртую.
При этом помним, что каждый раз должны менять направление движения.
Выше было сказано, что по такому правилу можно построить окружность определённого размера. Радиус такой окружности равен 5 клеткам.
Для построения окружностей других радиусов таким способом существуют другие правила.
А ещё клетчатая бумага даёт нам возможность представить, как можно замостить плоскость равными квадратами. Например, уложить квадратную кафельную плитку на пол или на стены.
Плоскость можно замостить не только квадратами, но и прямоугольниками.
Вы можете попробовать придумать способы укладки паркета из равных прямоугольников.
Давайте выполним задание. Можно ли замостить плоскость прямоугольника (или какую-либо площадь) фигурами, изображёнными на рисунке?
Далее мы решим несколько задач на разрезание. Задачи на разрезание увлекательны тем, что универсального метода их решения нет. Каждый, кто берётся за их решение, должен проявить свою смекалку и творческое мышление.
«Семь раз отмерь, один раз отрежь!» Эта пословица предостерегает вас от спешки при решении задач на разрезание.
Итак, задание. На рисунке изображён квадрат со стороной в 4 клетки. Разделите квадрат на 2 равные части так, чтобы линия разреза шла по сторонам клеток.
Способы разрезания квадрата на две части будем считать различными, если части квадрата, которые получены при одном способе разрезания, не равны частям, которые получены при другом способе. Сколько всего решений имеет задача?
Решение. Квадрат, который изображён на рисунке, содержит 16 клеток. Значит, при делении его на 2 равные части каждая из частей будет состоять из 8 клеток.
Отметим, что задача на разрезание на 2 или несколько одинаковых частей решена верно, если эти части будут одинаковыми по форме, то есть их можно наложить одна на другую так, что они совпадут (при этом разрешается наложить их наизнанку).
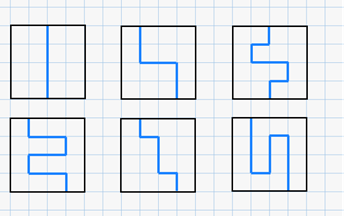
Выполним ещё одно задание. Разделите фигуры, изображённые на рисунке, на 2 равные части. Разрезать можно только по линиям клеток.
Задачами на разрезание увлекались многие учёные с древнейших времён. Решения многих простых задач на разрезание были найдены ещё древними греками, китайцами, но первое научное сочинение на эту тему принадлежит перу Абул-Вефа, знаменитого персидского астронома десятого века, который жил в Багдаде.
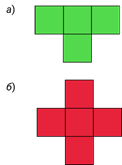
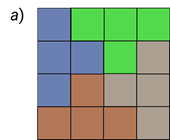
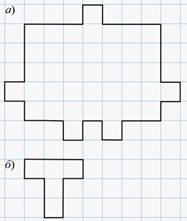
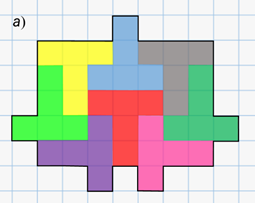
Выполним следующее задание. Раскрасьте фигуру, изображённую на рисунке а, буквами Т такой формы, как на рисунке б. Все буквы Т должны отличаться друг от друга по цвету.
Обратите внимание, что при выполнении этого задания букву Т можно поворачивать как угодно.
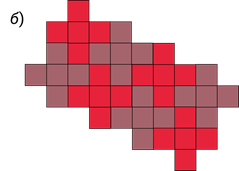
Ещё одно задание. Имеется лист клетчатой бумаги размером 10 на 10 клеток. Вырежьте из него как можно больше букв Т такой формы, как показано на рисунке.
Решение. Начнём вырезать фигуры в виде буквы Т из верхнего левого угла листа бумаги.
Источник