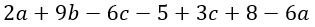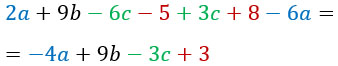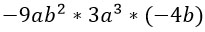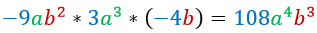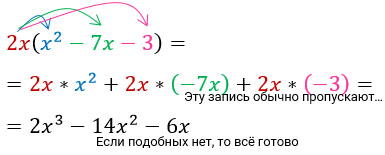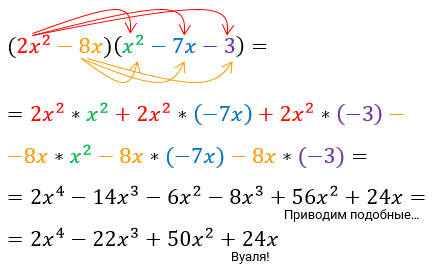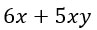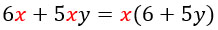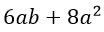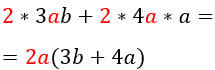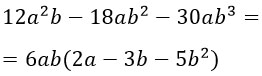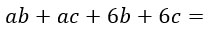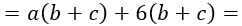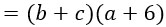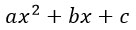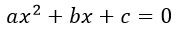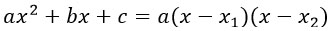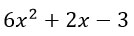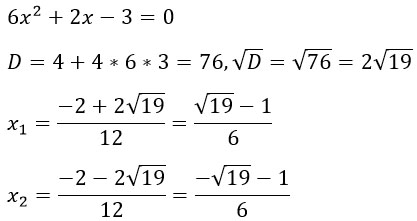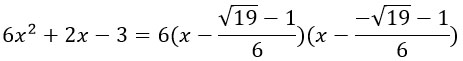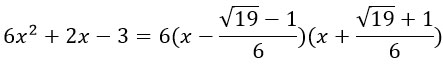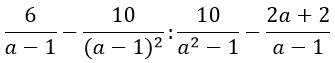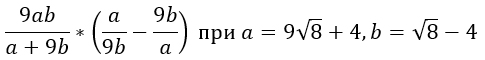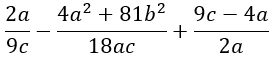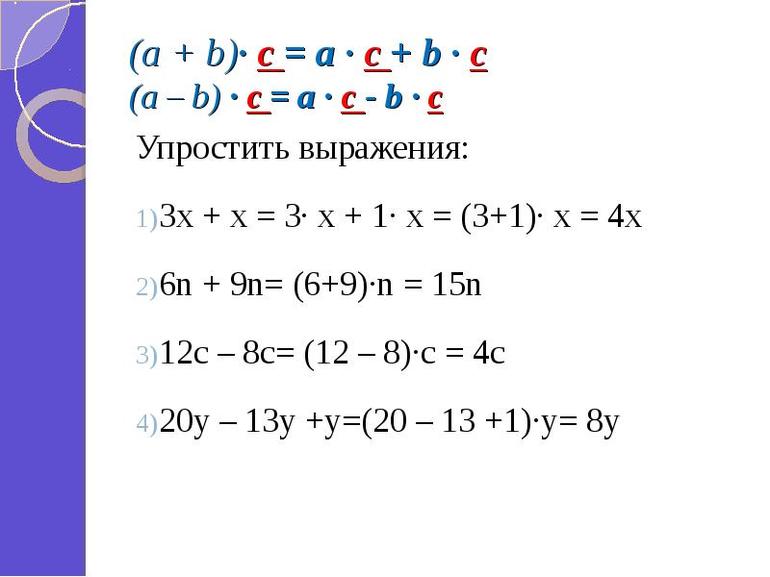Как решить уравнение способом упрощения

Упрощение выражений

Одно из самых распространенных заданий в алгебре звучит так: «Упростите выражение». Сделать это можно используя один из ниже перечисленных приемов, но чаще всего тебе потребуется их комбинация.

Приведение подобных слагаемых.

Это самый простой из приемов. Подобными называются те слагаемые, у которых одинаковая буквенная часть. Например, подобными будут выражения 5а и -6а; -3ху и 3ух; 2 и 10. Так вот. Складывать можно только подобные слагаемые; если буквенная часть у слагаемых различна, то такие слагаемые складывать уже нельзя. Согласись, если в жизни мы будем складывать яблоки с гвоздями, то у нас какая-то дичь получится) В математике точно так же.

Для примера упростим такое выражение:

Подобные слагаемые я выделю разными цветами и посчитаю. Кстати, знак перед слагаемым относится к этому слагаемому.

Как видишь, больше одинаковых буквенных частей нет. Выражение упрощено.

Умножение одночленов и многочленов.

Не буду спорить — числа ты умножать умеешь. А если к ним добавятся буквы, степени, скобки?

Одночлен — это выражение, состоящее из произведения чисел, букв, степеней, причем необязательно должно быть всё сразу. Удивительно, но просто число 5 тоже является одночленом, так же как и одинокая переменная х.

При умножении одночленов используют правила умножения степеней.

Перемножим три одночлена:

Разными цветами выделю то, что буду последовательно перемножать.

Многочлен — это сумма одночленов.

Чтобы умножить одночлен на многочлен выражение за скобками умножить на каждое слагаемое в скобках. Подробности в следующем примере.

Осталось вспомнить умножение многочлена на многочлен. При таком вот умножении надо каждое слагаемое в первых скобках умножить на каждое слагаемое во вторых скобках, результаты сложить или вычесть в зависимости от знаков слагаемых.

Вынесение общего множителя за скобки.

Разбираться будем на примере.

Дано такое выражение:

Что общего у этих двух слагаемых? Правильно, в них обоих присутствует множитель x. Он и будет являться общим множителем, который надо вынести за скобку.

Возьмем другой пример.

Оба числа в слагаемых делятся на 2, значит число 2 — общий множитель. Но еще в этих одночленах есть одинаковая буква а — одна в первой степени, другая — во второй. Берем ее в меньшей степени, т.е. в первой, — это и будет второй общий множитель. В общем, получится вот такая запись:

Ну и давайте третий пример, только уже без комментариев.

Проверить правильность вынесения общего множителя за скобки можно путем раскрытия скобок (умножением).

Разложение многочлена на множители способом группировки.

Если надо разложить многочлен на множители, то способ группировки тебе пригодится.

Сгруппировать выражения можно лишь путем вынесения общих множителей за скобку. Но сделать это нужно так, чтобы скобки в итоге получились одинаковые. Зачем? Да затем, чтобы потом эти скобки вынести за другие скобки.

На примере будет яснее)

Беру пример самый простой, чисто для понимания того, что надо делать.

В первых двух слагаемых общим множителем является переменная а: выносим ее за скобку. Во вторых двух слагаемых общим множителем является число 6. Его тоже выносим за скобки.

Видишь получились две одинаковые скобки? Теперь они являются общим множителем. Выносим их за скобку и получаем милое произведение двух скобок:

Разложение квадратного трехчлена на множители.

Пусть дан квадратный трехчлен:

Чтобы разложить его на множители надо решить квадратное уравнение

Далее корни уравнения х₁ и х₂ подставить в следующую формулу:

Возьмем вот такой трехчлен:

Найдем корни квадратного уравнения.

Подставим их в формулу для разложения квадратного трехчлена на множители:

Что-то слишком много минусов во второй скобке. Чуть-чуть преобразуем ее:

Еще могут тебе пригодится:

— умение сокращать дроби;

А вот такие задания могут тебе встретится на экзамене.

2) Найти значение выражения при заданных значениях переменных:

3) Найти значение выражения при заданных значениях переменных:

Подобных заданий много — их все не уместишь)

Источник

Упрощение выражений

Содержание

В математическом мире существует большое количество выражений, которых трудно решить без упрощения. Помимо этого, упрощение математических примеров используется для того, чтобы быстрее и правильнее решить задание.

Давайте рассмотрим пример, и не забывайте, что для этого нам понадобятся знания правил умножения, вычитания и сложения:

В данном случае, сначала мы можем посчитать сумму в скобках, а затем умножить на 3. Но далеко не всегда такой способ будет удобным при решении задач. Если цифры будут слишком большими – это будет попросту неудобно. Для облегчения решения нам нужно будет упростить данное выражение. Теперь рассмотрим пример его упрощения:

Сейчас мы видим, что выражение значительно изменилось. При этом, ответ будет точно таким же, как и в первом случае. Такой вид выражения не только легче и быстрее решать, но и помогает избежать ошибок при вычислении. Итак, как же правильно следует применять правила упрощения выражений и как решать уравнения с их помощью?

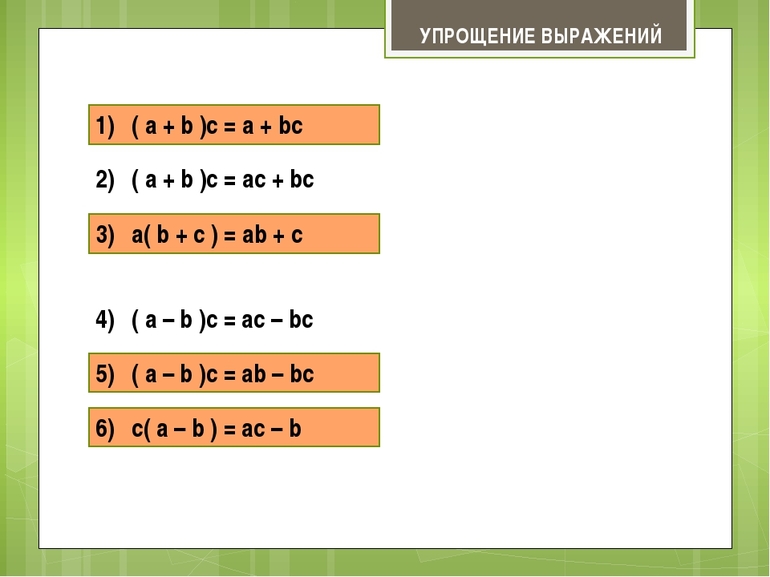
Правила упрощения

Существует всего два правила по упрощению выражений с умножением. Их называют распределительными свойствами умножения относительно сложения и вычитания. Давайте их разберем:

Для того, чтобы умножить сумму на число, нужно умножить на это число первое и второе слагаемое, а затем сложить получившиеся произведения.

С помощью букв данное правило записывают так: $(a+b)\cdot c=ac+bc$

Если нам нужно умножить разность на число, то следует умножить на это число уменьшаемое и вычитаемое, а потом из первого произведения вычесть второе.

Буквенное выражение данного свойства выглядит следующим образом: $(a-b)\cdot c=ac-bc$

Решение уравнений с применением упрощения выражений

Правила упрощения выражений работают и в обратную сторону, то есть позволяют вынести разность или сумму в скобки, а число, на которое нужно умножить – за скобки. Именно поэтому их используют для решения уравнений. Разберем на примере:

Для того, чтобы сложить два числа с $x$, нам нужно применить уже изученное нами распределительное свойство:

Благодаря данному упрощению мы сможем до конца решить наше уравнение:

Источник

Упрощения выражений — формулы и примеры для 5 класса

Общие сведения

Принцип решения любой математической задачи основан на получении оптимального ответа, который в дальнейшем возможно будет применить для других целей (доказательства теорем, тождеств, получения промежуточных величин). Оптимизация результата состоит из операций, имеющих собственный приоритет. Последний соответствует порядковому номеру элемента в списке:

1. Раскрытие скобок.
2. Возведение в степень, которая может быть целой и представленной в виде обыкновенной дроби (корень).
3. Произведение.
4. Частное или деление.
5. Сумма.
6. Разность.

В первом случае компоненты выражения группируются посредством скобок. В математике принято использовать только круглые, т. е. «()». Однако допускаются квадратные «[]», но некоторые начинающие математики иногда группируют элементы выражения при помощи фигурных скобок «<>». Это делать не рекомендуется, поскольку последние обозначают в дисциплинах с физико-математическим уклоном общее решение.

Иногда новички не знают, что возведение в степень и извлечение корня являются двумя эквивалентными операциями. Это утверждение легко доказывается. Например, квадратный корень из 36 эквивалентен 6. Знак радикала можно заменить степенью, имеющей вид обыкновенной или десятичной дроби, т. е. (36)^(½)=√36=6.

Произведение не всегда обладает высшим приоритетом, чем деление. Для удобства вычислений можно сначала разделить, а затем умножить. Например, требуется найти значение выражения «3*81:9». Его можно решить, основываясь на приоритетах или удобстве вычислений (оптимизации). Для сравнения расчетов нужно решить равенство двумя способами:

При решении получены одинаковые результаты. Следует отметить, что простой метод — второй. Операции сложения и вычитания имеют одинаковый приоритет. Упростить выражение — означает, что необходимо преобразовать его из сложной формы представления в простую. Иными словами, операция называется оптимизацией результата.

Оптимизация выражений применяется при решении уравнений (равенств с неизвестными величинами) любой сложности и доказательства теорем. Это базовые знания, необходимые для упрощения выражений в 5 классе.

Базовые знания

Для освоения определенного направления в любой дисциплине необходимы определенные знания. Например, невозможно выполнить умножение одного числа на другое, не зная таблицы умножения. Это касается и оптимизации тождеств. Основные элементы теории, которые нужно знать для выполнения операции:

1. Приведение общих компонентов.
2. Правила раскрытия скобок.
3. Работа со степенями.
4. Действия над знаменателями обыкновенных дробей и их сокращение.
5. Соотношения сокращенного умножения.

По этим пунктам можно упрощать алгебраические целочисленные и дробные выражения любой сложности. Однако каждый из элементов необходимо разобрать подробно, чтобы не совершать ошибок при расчетах.

Приведение подобных элементов

Практически во всех заданиях нужно складывать общие элементы, полученные при расчетах или раскрытии скобок. Для этой операции необходимо руководствоваться следующими правилами:

1. Приведению подлежат только эквивалентные компоненты.
2. Операция выполняется только при арифметическом сложении и вычитании, а не делении и умножении.
3. Компоненты равные по модулю, но противоположные по знаку, уничтожаются, т. к. в сумме дают нулевое значение.
4. В любом выражении можно использовать противоположные числа, поскольку их общее значение не влияет на результат.

В первом случае нужно привести пример тождества следующего вида: 2+5t+4+5t^2+2t-4t^2. Чтобы его упростить, необходимо сгруппировать подобные компоненты, т. е. (2+4)+(5t+2t)+(5t^2-4t^2). Далее следует сложить компоненты между собой, т. е. 6+7t+t^2.

Группу «5t^2-4t^2» можно назвать операцией сложения, хотя на самом деле она называется разностью, которую записывают и в виде суммы: 5t^2+(-4t^2). Раскрывая скобки в последнем тождестве, можно получить упрощенную форму: 5t^2-4t^2. Далее необходимо ознакомиться с правилами раскрытия скобок.

Раскрытие скобок

Операция раскрытия скобок для выполнения дальнейших вычислений очень часто применяется в различных дисциплинах с физико-математическим уклоном. Она осуществляется по следующим правилам:

1. Произведение на сумму или разность: r(s+t)=rs+rt или r(s-t)=rs-rt.
2. Деление суммы или разности: (s+t)/r=s/r+t/r или (s-t)/r=s/r-t/r.
3. Сгруппировать любые компоненты и поменять их местами с сохранением логики тождества: 3+4+11+7+19+33+23=(3+4+23)+(19+11)+(7+33)=30+30+40=100.

В первом и втором случаях операции называют вынесением общего множителя за скобки. Последнее правило группировки действует не на все компоненты, т. е невозможно выполнить объединение 2 и 3 элементов (5 и 4) в выражении «4:5+4-1+7». Для доказательства следует решить его двумя способами:

Выражение, решенное первым и вторым способом, имеет различные ответы, поскольку 10,8>6[4/9]. Объяснение этому несоответствию — нарушение логики тождества. Следующим компонентом, составляющим базу для упрощения тождеств, является работа со степенями.

Работа со степенями

В математических тождествах иногда необходимо упростить степенные выражения. Однако большинство математиков-новичков делает много ошибок, поскольку не знают основных правил:

Нулевое значение в такой же степени является пустым множеством, т. е. его не существует. Cтепень может быть представлена в виде обыкновенной или десятичной дроби. В последнем случае для удобства ее необходимо перевести к первому типу. Если указано значение степенного показателя, равное 3/5, нужно величину возвести в куб, а затем изъять корень 5 порядка.

Оптимизация обыкновенных дробей

Практически во всех заданиях или тренажерах большая часть примеров представлена в виде обыкновенной дроби вида s/t, которую нужно сократить. Иногда необходимо произвести операции произведения или деления одной величины на другую (буквенное обозначение — s/t и w/v), а также сложения и вычитания. При последних операциях всегда необходимо приводить дробные тождества к общему знаменателю. Эта операция осуществляется следующим образом:

1. Если знаменатель одной дроби делится нацело на другой, следует оставить первый, записав множитель над второй величиной. Например, 4/5 + 4/25=(4*5+4*1)/25=24/25.
2. Когда v и t не делятся друг на друга, не имеют общих множителей, их нужно перемножить между собой, записав множители над числителями.
3. Если v и t содержат общие множители, единый знаменатель эквивалентен наименьшему общему кратному (НОК).

В последнем случае каждый знаменатель необходимо разложить на множители, затем перемножить между собой все неповторяющиеся компоненты. Следующим элементом, который необходимо для преобразования тождеств, являются формулы сокращенного умножения.

Сокращенное умножение

Для решения задач очень часто применяются формулы сокращенного умножения. В некоторых случаях тождества «собираются» в них или, наоборот, для сокращения нужно расписать элементы по множителям (правая часть равенства). Соотношения имеют следующий вид:

1. Квадрат суммы и разности двух чисел: (w+v)^2=w^2+2wv+v^2 и (w-v)^2=w^2-2wv+v^2.
2. Разность квадратов и кубов: w^2-v^2=(w+v)(w-v) w^3-v^3=(w-v)(w^2+wv+v^2).
3. Куб суммы компонентов и их разности: (w+v)^3=w^3+3wv^2+3vw^2+v^3 и (w-v)^3=w^3-3wv^2+3vw^2-v^3.

Cледует отметить, что в некоторых случаях к формуле сокращенного умножения тождество следует «подвести», воспользовавшись свойством отнимания и прибавления одного и того же значения. Например, необходимо из некоторого выражения (2t^2-60) выделить одну из формул. Это делается следующим образом:

1. Выносится общий множитель за скобки: 2(t^2-30).
2. Прибавляется и отнимается 6: 2(t^2-30+6-6).
3. Группируются элементы и записывается формула: 2(t^2-36+6)=2[(t-6)(t+6)+6].

Иногда в более сложных выражениях приходится применять несколько соотношений. Если тождество является дробью, обязательно следует проверить условие неравенства знаменателя нулевой величине. Для этой цели следует решить соответствующее уравнение, вычислив его корни. Последние должны привести к пустому множеству, т. к. на 0 делить нельзя. Вот именно их и необходимо исключить, записав условие, т. е. t!=-9.

Таким образом, для грамотной оптимизации математических выражений необходимо пользоваться рекомендациями специалистов, правилами и методиками, поскольку их несоблюдение могут существенно повлиять на результаты вычислений.

Источник