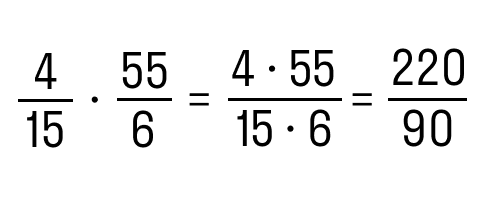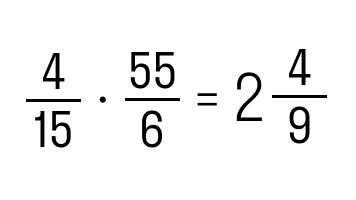Как решить умножение удобным способом

Умножение дробей: теория и практика

О чем эта статья:

5 класс, 6 класс

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление — в 5 классе уже это знают.

Дроби могут быть двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
2. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя:

Неправильной — ту, у которой числитель больше знаменателя или равен ему:

Такое число называют смешанным, читают как «пять целых одна четвертая», а записывают так: 5 1\4.

Основные правила дробей

• Если делитель равен нулю — у дроби нет значения
• Дробь равна нулю, если числитель равен нулю, а знаменатель — нет
• Две дроби a/b и c/d называют равными, если a * d = b * c.
• Если числитель и знаменатель умножить или разделить на одно и то же натуральное число — получится равная ей дробь.

Умножение дробных чисел

Рассмотрим несколько вариантов умножения обыкновенных дробей.

Как умножить дробь на дробь

Числитель равен произведению числителей обеих дробей, а знаменатель равен произведению знаменателей:

Важно проверить возможность сокращения — так решать будет легче:

Как умножить смешанные дроби

Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.

Как умножить дробь на натуральное число

Метод 1. Числитель умножить на натуральное число, а знаменатель оставить без изменения. Если в результате произведения получилась неправильная дробь, нужно выделить целую часть, то есть превратить неправильную в смешанную.

Метод 2. Знаменатель разделить на натуральное число, а числитель оставить прежним.

Этот способ будет удобнее предыдущего, если знаменатель делится на натуральное число без остатка.

Решение задач

Ребятам в 5 и 6 классе нужно практиковаться как можно чаще, чтобы решать такие примеры быстро и легко.

Задание 1. Выполнить умножение 2/17 на 5.

Как решаем: перемножим делимое и натуральное число.

Ответ:

Задание 2. Выполнить умножение 4/15 и 55/6.

Как решаем:

• перемножим числители между собой и знаменатели соответственно
  

• сократим полученное

• выделим целую часть

Ответ:

Задание 3. Выполнить умножение одной целой трех седьмых на шесть.

Как решаем:

• переводим смешанное число в неправильную дробь,
• умножаем делимое на натуральное число,
• сократим полученное,
• преобразуем в смешанное число.

Ответ:

Если вопрос не ждет и ответ нужно получить как можно быстрее, можно использовать онлайн калькулятор. Умножение будет быстрым и точным:

Источник

Свойства умножения и деления

О чем эта статья:

Свойства умножения

Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.

Узнаем, какие бывают свойства умножения и как их применять.

Переместительное свойство умножения

От перестановки мест множителей произведение не меняется.

То есть, для любых чисел a и b верно равенство: a * b = b * a.

Это свойство можно применять к произведениям, в которых больше двух множителей.

• 6 * 5 = 5 * 6 = 30;
• 4 * 2 * 3 = 3 * 2 * 4 = 24.

Сочетательное свойство умножения

Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.

То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).

3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30

3 * 2 * 5 = (3 * 2) * 5 = 6 * 5 = 30.

Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.

Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.

Распределительное свойство умножения относительно сложения

Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.

То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.

Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.

В обратную сторону распределительное свойство умножения относительно сложения звучит так:

Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Распределительное свойство умножения относительно вычитания

Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.

То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.

В обратную сторону распределительное свойство умножения относительно вычитания звучит так:

Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Свойство нуля при умножении

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.

Свойство единицы при умножении

Если умножить любое целое число на единицу, то в результате получится это же число.

То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.

Свойства деления

Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.

Основные свойства деления целых чисел

1. Деление на нуль невозможно.
2. Деление нуля на число: 0 : a = 0.
3. Деление равных чисел: a : a = 1.
4. Деление на единицу: a : 1 = a.
5. Для деления переместительное свойства не выполняется: a : b ≠ b : a.
6. Деление суммы и разности на число: (a ± b) : c = (a : c) ± (b : c).
7. Деление произведения на число:
   (a * b) : c = (a : c) * b, если a делится на c;
   (a * b) : c = a * (b : с), если b делится на c;
   (a * b) : c = a * (b : с) = (a : c) * b, если a и b делятся на c.
8. Деление числа на произведение:
   a : (b * c) = (a : b) * (1 : c) = (a : c) * (1 : b).

И еще одно важное свойство деления, которое проходят в 5 классе:

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.

Применим свойства деления на практике.

Пример 1

Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?

Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.

Пример 2

Вычислить: 500 * (100 : 5).

Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.

Ответ: 500 * (100 : 5) = 10000.

Пример 3

Упростить выражение: 27a – 16a.

Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 — 16) = a * 11 = 11a.

Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.

Источник

Порядок действий в математике

О чем эта статья:

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше ( )
меньше (

Порядок вычисления простых выражений

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:

• действия выполняются по порядку слева направо
• сначала выполняется умножение и деление, а затем — сложение и вычитание.

Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.

Что первое, умножение или деление? — По порядку слева направо.

Сначала умножение или сложение? — Умножаем, потом складываем.

Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить вычисление: 11- 2 + 5.

В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.

Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.

Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.

Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.

Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.

Например, в такой последовательности можно решить пример по действиям:

Действия первой и второй ступени

В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.

• Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.

С этими терминами правило определения порядка выполнения действий звучит так:

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.

Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.

И, как всегда, рассмотрим, как это работает на примере.

Пример 1. Вычислить (4 + 1) * 3 + 62 : 3 — 7.

В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.

Подставляем полученное значение в исходное выражение:

(4 + 1) * 3 + 36 : 3 — 7.

Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:

(4 + 1) * 3 + 36 : 3 — 7 = 3 * 3 + 36 : 3 — 7 = 9 + 12 — 7 = 14.

Ответ: (3 + 1) * 2 + 62 : 3 — 7 = 14.

У нас есть статья «знаки больше, меньше или равно», она может быть полезной для тебя!

Источник