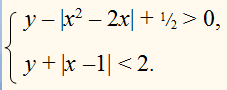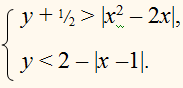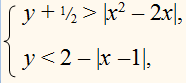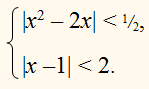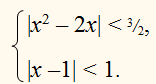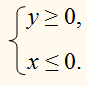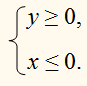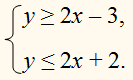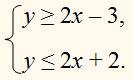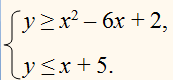Как решить систему неравенств с двумя переменными графическим способом

Содержание

Графическое решение неравенств, системы совокупностей неравенств с двумя переменными
Системы совокупностей неравенств с двумя переменными
Системы неравенств с двумя переменными
п.1. Алгоритм графического решения системы неравенств с двумя переменными
п.2. Примеры
Линейные неравенства с двумя переменными и их системы
Линейное неравенство с двумя переменными и его решение
Графическое представление линейного неравенства с двумя переменными
Графическое решение системы линейных неравенств с двумя переменными
Примеры
Уроки математики и физики для школьников и родителей
четверг, 17 октября 2019 г.
Урок 14. Система неравенств с двумя переменными

Графическое решение неравенств, системы совокупностей неравенств с двумя переменными

Пусть f(x,y) и g(x, y) – два выражения с переменными х и у и областью определения Х. Тогда неравенства вида f(x, y) > g(x, y) или f(x, y) g(x, y), поступают следующим образом. Сначала заменяют знак неравенства знаком равенства и находят линию, имеющую уравнение f(x,y) = g(x,y). Эта линия делит плоскость на несколько частей. После этого достаточно взять в каждой части по одной точке и проверить, выполняется ли в этой точке неравенство f(x, y) > g(x, y). Если оно выполняется в этой точке, то оно будет выполняться и во всей части, где лежит эта точка. Объединяя такие части, получаем множество решений.

Задача. Решить графически неравенство y > x.

Решение. Сначала заменим знак неравенства знаком равенства и построим в прямоугольной системе координат линию, имеющую уравнение y = x.

Эта линия делит плоскость на две части. После этого возьмем в каждой части по одной точке и проверим, выполняется ли в этой точке неравенство y > x.

Задача. Решить графически неравенство
х2 + у2 £ 25.

Решение. Сначала заменим знак неравенства знаком равенства и проведем линию х2 + у2 = 25. Это окружность с центром в начале координат и радиусом 5. Полученная окружность делит плоскость на две части. Проверяя выполнимость неравенства х2 + у2 £ 25 в каждой части, получаем, что графиком является множество точек окружности и части плоскости внутри окружности.

Системы совокупностей неравенств с двумя переменными

Система неравенств представляет собой конъюнкцию этих неравенств. Решением системы является всякое значение (x, y), которое обращает каждое из неравенств в истинное числовое неравенство. Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих данную систему.

Совокупность неравенств представляет собой дизъюнкцию этих неравенств. Решением совокупности является всякое значение (x, y), которое обращает в истинное числовое неравенство хотя бы одно из неравенств совокупности. Множество решений совокупности есть объединение множеств решений неравенств, образующих совокупность.

Задача. Решить графически систему неравенств

Решение. Сначала заменяем знак неравенства знаком равенства и проводим в одной системе координат линии у = х и х2 + у2 = 25. Решаем каждое неравенство системы.

Графиком системы будет множество точек плоскости, являющихся пересечением (двойная штриховка) множеств решений первого и второго неравенств.

Задача. Решить графически совокупность неравенств

Решение. Сначала заменяем знак неравенства знаком равенства и проводим в одной системе координат линии у = х + 4 и х2 + у2 = 16. Решаем каждое неравенство совокупности. Графиком совокупности будет множество точек плоскости, являющихся объединением множеств решений первого и второго неравенств.

Упражнения для самостоятельной работы

1. Решите графически неравенства: а) у > 2x; б) у 9; г) x2 + y2 £ 4.

2. Решите графически системы неравенств:

а) в)

б) г)

3. Решите графически совокупности неравенств:

а) в)

б) г)

Источник

Системы неравенств с двумя переменными

п.1. Алгоритм графического решения системы неравенств с двумя переменными

Найти на координатной плоскости множество решений системы неравенств: $$ \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. $$ Множество решений – сегмент круга, отсекаемый отрезком AB. Сам отрезок в множество решений не входит.

п.2. Примеры

Пример 1. Найдите на координатной плоскости множество решений системы неравенств.

Выразим y(x) в явном виде

Строим прямые, заштриховываем области над ними, находим пересечение.

Выразим y(x) в явном виде

Заштриховываем область под первой параболой и над второй параболой.

Выразим y(x) в явном виде

Строим гиперболу и прямую. Заштриховываем области под гиперболой и над прямой.

Заштриховываем области вне первой окружности и внутри второй.

Находим пересечение – кольцо.

Пример 2. Задайте системой неравенств треугольник с вершинами
A(2; 3), B(4; 4), C(3; 0)
Уравнения прямых, на которых лежат стороны треугольника:

Источник

Линейные неравенства с двумя переменными и их системы

Линейное неравенство с двумя переменными и его решение

Неравенство вида ax+by $ \begin \lt \\ \gt \\ \le \\ \ge \end $ c , где a, b, c — данные числа, называется линейным неравенством с двумя переменными x и y.

Например: $2x+5y \lt 6; -x+1, 5y \ge 0; \frac<1> <2>x-8y \gt 7$

Решением неравенства с двумя переменными называется упорядоченная пара значений переменных (x,y), обращающая это неравенство в истинное выражение.

Например: для неравенства $2x+5y \lt 6$

пара (-1;-2) является решением, т.к. $2\cdot(-1)+5 \cdot (-2) = -12 \lt 6$ – истина

пара (1;2) не является решением, т.к. $2\cdot1+5\cdot2=12 \not\lt 6$ – ложь

Графическое представление линейного неравенства с двумя переменными

Графическим представлением линейного неравенства с двумя переменными вида ax+by$ \begin \lt \\ \gt \\ \le \\ \ge \end $ c является полуплоскость с границей ax+by = c .

Для строгого неравенства граница не входит в представление, для нестрогого неравенства – входит.

Графическое решение системы линейных неравенств с двумя переменными

Графическим решением системы линейных неравенств с двумя переменными является пересечение их графических представлений на плоскости.

Пересечение двух множеств – это множество, которому принадлежат только те элементы, которые одновременно входят в оба множества.

Пересечение обозначают знаком $\cap$.

Найдём графическое решение системы линейных неравенств:

Решением является треугольник ABC, где A(-1;2), B(0;4), C(2;0).

Примеры

Пример 1. Найдите графическое представление линейного неравенства:

Представление – полуплоскость под границей, сама граница не входит

Представление – полуплоскость под границей, сама граница входит

Представление – полуплоскость справа от границы, сама граница входит

Представление – полуплоскость под границей, сама граница не входит

Пример 2*. Найдите графическое решение системы линейных неравенств:

Решением является квадрат ABCD, где A(-3;-1), B(0;2), C(3;1), D(0;-4)

Пример 3*. Автоперевозчику поступил заказ на перевозку 30 т груза. У него есть 5 машин грузоподъёмностью 3 т и 5 машин грузоподъёмностью 5 т.

Расход топлива для каждого типа грузовиков соответственно 20 и 24 л, общий расход не должен превышать 170 л.

Подберите состав грузовиков для выполнения заказа.

Пусть x — количество грузовиков по 3т, y – по 5т.

По условию задачи:

$$ <\left\< \begin 3x+5y \ge 30 \\ 20x+24y \le 170 \\ x \le 5 \\ y \le 5 \end \right.> $$

Решением системы неравенств является заштрихованный треугольник. Единственным целочисленным решением является точка A(2;5) Таким образом, для выполнения заказа нужно 2 грузовика по 3т и 5 грузовиков по 5т.

Их суммарная грузоподъёмность: $3 \cdot 2+5 \cdot 5 = 31 \gt 30$ достаточна

Суммарный расход топлива: $ 20 \cdot 2+24 \cdot 5 = 160 \lt 170 $ не превышает лимит

Ответ: 2 грузовика по 3т и 5 грузовиков по 5т

Источник

Уроки математики и физики для школьников и родителей

четверг, 17 октября 2019 г.

Урок 14. Система неравенств с двумя переменными

то из неравенств

Целыми числами, удовлетворяющими этому неравенству, являются лишь 0 и 1 , поэтому система

1) Если у = 0 , то система примет следующий вид :

Проверка показывает, что первому неравенству удовлетворяют

образуют решения исходной системы неравенств .

2) Если у = 1 , то система примет следующий вид :

Графический метод решения систем неравенств с двумя переменными.

Суть метода решений системы неравенств с двумя переменными проста. Находим решение каждого неравенства в отдельности, изображаем решения на одной координатной плоскости и ищем пересечение этих решений.

Решить графически систему неравенство