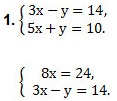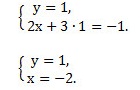Как решить системное уравнение способом сложения

6.9.3. Решение систем линейных уравнений методом сложения.

Чтобы решить систему линейных уравнений с двумя переменными методом сложения, надо:

1) умножить левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в уравнениях стали противоположными числами;

2) сложить почленно полученные уравнения и найти значение одной из переменных;

3) подставить найденное значение одной переменной в одно из данных уравнений и найти значение второй переменной.

Если в данной системе коэффициенты при одной переменной являются противоположными числами, то решение системы начнём сразу с пункта 2).

Примеры. Решить систему линейных уравнений с двумя переменными методом сложения.

Так как коэффициенты при у являются противоположными числами (-1 и 1), то решение начинаем с пункта 2). Складываем уравнения почленно и получим уравнение 8х = 24. Вторым уравнением системы можно записать любое уравнение исходной системы.

Найдём х и подставим его значение во 2-ое уравнение.

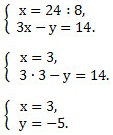
Решаем 2–ое уравнение: 9-у = 14, отсюда у = -5.

Сделаем проверку. Подставим значения х = 3 и у = -5 в первоначальную систему уравнений.

Примечание . Проверку можно сделать устно и не записывать, если наличие проверки не оговорено в условии.

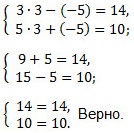
Ответ: (3; -5).

Если мы умножим 1-ое уравнение на (-2), то коэффициенты при переменной х станут противоположными числами:

Сложим эти равенства почленно.

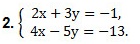
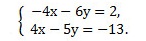
Мы получим равносильную систему уравнений, в которой 1-ое уравнение есть сумма двух уравнений прежней системы, а 2-м уравнением системы мы запишем 1-ое уравнение исходной системы (обычно записывают уравнение с меньшими коэффициентами):

Находим у из 1-го уравнения и полученное значение подставляем во 2-ое.

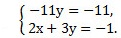
Решаем последнее уравнение системы и получаем х = -2.

Ответ: (-2; 1).

Сделаем коэффициенты при переменной у противоположными числами. Для этого все члены 1-го уравнения умножим на 5, а все члены 2-го уравнения на 2.

Подставим значение х=4 во 2-ое уравнение.

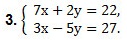
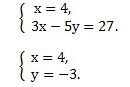
3 · 4 — 5у = 27. Упростим: 12 — 5у = 27, отсюда -5у = 15, а у = -3.

Источник

Линейные уравнения. Решение систем линейных уравнений. Способ сложения.

Метод сложения – решая системы линейных уравнений методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ, где в одном из уравнений есть лишь одна переменная.

Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:

1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.

2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.

3. Далее необходимо решить линейное уравнение, которое мы получили и найти решение системы.

Решение системы — это точки пересечения графиков функции.

Рассмотрим на примерах.

Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (–1 и 1). В таком случае уравнения легко сложить почленно:

Действия, которые обведены красным цветом, выполняем в уме.

Результатом почленного сложения стало исчезновение переменной y. Именно в этом и В этом, собственно, и заключается смысл метода – избавиться от 1-ой из переменных.

Далее очень легко: 3x + 12 = 0 → x = -4 – подставляем в 1-е уравнение системы (можете и во 2-у, но это не так удобно, так как во втором уравнении числа больше):

В виде системы решение выглядит где-то так:

В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус — когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях. А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.

Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:

Нужно подобрать число, которое можно поделить и на 3 и на 4, при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное. Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .

1-е уравнение умножаем на ,

3-е уравнение умножаем на ,

Далее из 1-го уравнения почленно вычитаем 2-е.

Обратите внимание, что можно делать и наоборот – из 2-го уравнения вычесть 1-е, разницы нет.

Далее подставляем, найденное значение в любое из уравнений системы, к примеру, в 1-е:

Ответ: .

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Решить систему уравнений

Немного теории.

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ \left\< \begin 3x+y=7 \\ -5x+2y=3 \end \right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ \left\< \begin y = 7—3x \\ -5x+2(7-3x)=3 \end \right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 \Rightarrow -5x+14-6x=3 \Rightarrow -11x=-11 \Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 \cdot 1 \Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ \left\< \begin 2x+3y=-5 \\ x-3y=38 \end \right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ \left\< \begin 3x=33 \\ x-3y=38 \end \right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение \( x-3y=38 \) получим уравнение с переменной y: \( 11-3y=38 \). Решим это уравнение:
\( -3y=27 \Rightarrow y=-9 \)

Таким образом мы нашли решение системмы уравнений способом сложения: \( x=11; y=-9 \) или \( (11; -9) \)

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.

Источник

Решение системы уравнений (ЕГЭ 2022)

Решение уравнений и систем уравнений — на самый легкий, но зато универсальный метод решения задач.

Этим методом можно решить буквально любую задачу.

Поэтому им стоит овладеть в совершенстве.

Читай эту статью и ты научишься решать системы уравнений.

Решение систем уравнений — коротко о главном

Определение:

Система уравнений –это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

Объединяем уравнения в систему с помощью фигурной скобки:

3 метода решения систем уравнений:

1. Метод подстановки — самый простой, но трудоемкий;
2. Графический метод — самый неточный, годится только для некоторых линейных уравнений;
3. Метод сложения — наиболее эффективный из трех, но не всегда удобен.

А теперь подробнее…

Что такое система уравнений

Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться, такую группу уравнений мы называем системой.

Например, ты хочешь сходить на концерт любимой группы вечером. Для этого тебе нужно согласие мамы и папы одновременно. Мама запретит – уже не идешь. 🙂

Объединяем уравнения в систему с помощью фигурной скобки:

\( \left\< \beginУравнение\ 1\\Уравнение\ 2\\Уравнение\ 3\\…\end \right.\)

3 метода решения систем уравнений

1. Метод подстановки

Нужно в одном из уравнений выразить одну переменную через другие, а затем полученное выражение подставить в остальные уравнения вместо этой переменной, повторять подобную процедуру пока не будут найдены все переменные.

2. Графический метод

Если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.

Графический метод – самый неточный. Практически его можно применять только для систем линейных уравнений (вида \( y=ax+b\)), графиками которых являются прямые.

Если же хотя бы одно из уравнений имеет более сложный вид (содержит квадрат, корень, логарифм и т.д.), то использовать графический метод не рекомендуется.

3. Метод сложения

Метод сложения основан на следующем: если сложить левые части двух (или больше) уравнений, полученное выражение будет равно сложенным правым частям этих же уравнений.

Но ни в коем случае не наоборот:

\( a+c=b+d\text< >\triangleleft \ne \triangleright \text< >\left\< \begina=b\\c=d\end \right.\)

Источник