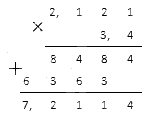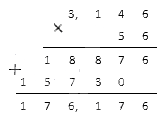Как решить рациональным способом дроби

Действия с рациональными числами: правила, примеры, решения

Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.

Действие сложения рациональных чисел

Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.

Сформулируем правила сложения рациональных чисел:

Сложение нуля с отличным от него рациональным числом

Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .

Пара простых примеров: сумма рационального числа 2 , 1 и числа 0 равно 2 , 1 и: 6 4 5 + 0 = 6 4 5 .

Сложение противоположных рациональных чисел

Сумма противоположных чисел равна нулю.

Данное правило можно записать в виде: a + ( — a ) = 0 (для любого рационального числа a ).

К примеру, числа 45 , 13 и — 45 , 13 являются противоположными, т.е. их сумма равно нулю: 45 , 13 + ( — 45 , 13 ) = 0 .

Сложение положительных рациональных чисел

В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.

Необходимо произвести сложение рациональных чисел: 0 , 6 и 5 9 .

Решение

Выполним перевод десятичной дроби в обыкновенную и тогда: 0 , 6 + 5 9 = 6 10 + 5 9 .

Осуществим сложение дробей с разными знаменателями:

6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45

Ответ: 0 , 6 + 5 9 = 1 7 45 .

Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.

Сложение рациональных чисел с разными знаками

Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.

Необходимо осуществить сложение рациональных чисел с разными знаками 8 , 2 и — 2 3 4 .

Решение

Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: | 8 , 2 | = 8 , 2 и | — 2 3 4 | = 2 3 4 . Проведя сравнение модулей — рациональных чисел, получим: 8 , 2 > 2 3 4 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8 , 2 — 2 3 4 = 8 2 10 — 2 3 4 = 5 9 20 .

Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8 , 2 + ( — 2 3 4 ) = 5 9 20 .

Сложение отрицательных рациональных чисел

Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.

Необходимо произвести сложение чисел: — 4 , 0203 и — 12 , 193 .

Решение

Модули заданных чисел соответственно равны: 4 , 0203 и 12 , 193 . Сложим их:

​​​​​​

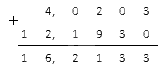
Полученному результату присваиваем знак минус: — 16 , 2133 .

Ответ: ( — 4 , 0203 ) + ( — 12 , 193 ) = — 16 , 2133 .

Действие вычитания рациональных чисел

Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c + b = a следует, что a — b = c и a — c = b . И наоборот: из равенств a — b = c и a — c = b следует, что c + b = a .

При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.

Необходимо вычислить разность рациональных чисел: 4 , ( 36 ) – 1 5 .

Решение

Сначала переведем периодическую десятичную дробь в обыкновенную: 4 , ( 36 ) = 4 + ( 0 , 36 + 0 , 0036 + … ) = 4 + 0 , 36 1 — 0 , 01 = 4 + 36 99 = 4 + 4 11 = 4 4 11

Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4 , ( 36 ) — 1 5 = 4 4 11 — 1 5 = 4 + 4 11 — 1 5 = 4 + 20 55 — 11 55 = 4 + 9 55 = 4 9 55

Ответ: 4 , ( 36 ) — 1 5 = 4 9 55

В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + ( — b ) .

Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: ( a + ( — b ) ) + b = a + ( ( — b ) + b ) = a + 0 = a . Отсюда в силу смысла действия вычитания следует, что сумма a + ( — b ) есть разность чисел a и b .

Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7

Решение

Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. — 5 3 7 . Тогда: 2 7 — 5 3 7 = 2 7 + — 5 3 7

Далее произведем сложение рациональных чисел с разными знаками: 2 7 + — 5 3 7 = — 5 3 7 — 2 7 = — 5 3 7 — 2 7 = — 5 1 7

Ответ: 2 7 + — 5 3 7 = — 5 1 7

Действие умножения рациональных чисел

Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.

Умножение на нуль

Произведение любого рационального числа a на нуль есть нуль.

Используя переместительное свойство умножения, получим: 0 · а = 0 .

К примеру, умножение рационального числа 7 13 на 0 даст 0 . Перемножив отрицательное рациональное число — 7 1 8 и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0 · 0 = 0 .

Умножение на единицу

Умножение любого рационального числа a на 1 дает число a .

Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.

К примеру, умножение рационального числа 5 , 46 на 1 даст в итоге число 5 , 46 .

Умножение взаимообратных чисел

Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а · а — 1 = 1 .

К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.

Умножение положительных рациональных чисел

В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.

Необходимо вычислить произведение положительных рациональных чисел 0 , 5 и 6 25 .

Решение

Представим заданную десятичную дробь в виде обыкновенной 0 , 5 = 5 10 = 1 2 .

Далее произведем умножение обыкновенных дробей: 1 2 · 6 25 = 6 50 = 3 25 .

Ответ: 0 , 5 · 6 25 = 3 25

Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.

Необходимо вычислить произведение рациональных чисел 2 , 121 и 3 , 4 .

Решение

Перемножим десятичные дроби столбиком:

Ответ: 2 , 121 · 3 , 4 = 7 , 2114

В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.

Умножение рациональных чисел с разными знаками

Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.

Необходимо найти произведение чисел: — 3 3 8 и 2 1 2

Решение

Согласно вышеуказанному правилу получим: — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2

Заменим смешанные дроби неправильными и найдем искомое произведение: — 3 3 8 · 2 1 2 = — 27 8 · 5 2 = — 135 16 = — 8 7 16

Ответ: — 3 3 8 · 2 1 2 = — 8 7 16

Умножение отрицательных рациональных чисел

Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.

Необходимо найти произведение отрицательных рациональных чисел — 3 , 146 и — 56 .

Решение: модули заданных чисел соответственно равны 3 , 146 и 56 .

Перемножим их столбиком:

Полученный результат и будет являться искомым произведением.

Ответ: ( — 3 , 146 ) · ( — 56 ) = 176 , 176

Деление рациональных чисел

Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b · c = a следует, что a : b = c и a : c = b . И наоборот: из равенств a : b = c и a : c = b следует, что b · c = a .

На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.

Разделить число а на число b , отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a : b = a · b — 1 .

Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств ( a · b — 1 ) · b = a · ( b — 1 · b ) = a · 1 = a , которая и доказывает равенство a : b = a · b — 1 .

Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.

Необходимо выполнить действие деления 3 1 3 : — 1 1 6

Решение

Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: — 1 1 6 = — 7 6 .

Число, обратное этой дроби, будет: — 6 7 . Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 3 1 3 — 1 1 6 = 3 1 3 · — 6 7 = 10 3 · ( — 6 7 ) = — ( 10 3 · 6 7 ) = — 20 7 = — 2 6 7

Ответ: 3 1 3 : — 1 1 6 = — 2 6 7

Источник

Дробно-рациональные уравнения

Что такое дробно-рациональные уравнения

Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:

при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.

Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.

9 x 2 — 1 3 x = 0

1 2 x + x x + 1 = 1 2

6 x + 1 = x 2 — 5 x x + 1

Уравнения, которые не являются дробно-рациональными:

Как решаются дробно-рациональные уравнения

В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.

Алгоритм действий при стандартном способе решения:

1. Выписать и определить ОДЗ.
2. Найти общий знаменатель для дробей.
3. Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
4. Записать уравнение со скобками.
5. Раскрыть скобки для приведения подобных слагаемых.
6. Найти корни полученного уравнения.
7. Выполним проверку корней в соответствии с ОДЗ.
8. Записать ответ.

Пример 1

Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:

x x — 2 — 7 x + 2 = 8 x 2 — 4

Начать следует с области допустимых значений:

x 2 — 4 ≠ 0 ⇔ x ≠ ± 2

Воспользуемся правилом сокращенного умножения:

x 2 — 4 = ( x — 2 ) ( x + 2 )

В результате общим знаменателем дробей является:

Выполним умножение каждого из членов выражения на общий знаменатель:

x x — 2 — 7 x + 2 = 8 x 2 — 4

x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )

После сокращения избавимся от скобок и приведем подобные слагаемые:

x ( x + 2 ) — 7 ( x — 2 ) = 8

x 2 + 2 x — 7 x + 14 = 8

Осталось решить квадратное уравнение:

Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:

Примеры задач с ответами для 9 класса

Требуется решить дробно-рациональное уравнение:

x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0

x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0

Определим область допустимых значений:

О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2

x 2 + 7 x + 10 ≠ 0

D = 49 — 4 · 10 = 9

x 1 ≠ — 7 + 3 2 = — 2

x 2 ≠ — 7 — 3 2 = — 5

Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:

a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Сократим дроби, избавимся от скобок, приведем подобные слагаемые:

x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —

— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0

x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0

x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0

2 x 2 + 9 x — 5 = 0

Потребуется решить квадратное уравнение:

2 x 2 + 9 x — 5 = 0

Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.

Дано дробно-рациональное уравнение, корни которого требуется найти:

4 x — 2 — 3 x + 4 = 1

В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:

4 \ ( x + 4 ) x — 2 — 3 \ ( x — 2 ) x + 4 — 1 \ ( x — 2 ) ( x + 4 ) = 0

4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0

4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0

x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0

Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:

— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0

Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:

( x — 2 ) ( x + 4 ) ≠ 0

Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:

— x 2 — x + 30 = 0 _ _ _ · ( — 1 )

Получилось квадратное уравнение, которое можно решить:

Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.

Нужно решить дробно-рациональное уравнение:

x + 2 x 2 — 2 x — x x — 2 = 3 x

На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:

x + 2 \ 1 x ( x — 2 ) — x \ x x — 2 — 3 \ ( x — 2 ) x = 0

x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0

x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0

— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0

Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.

— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )

Корни квадратного уравнения:

x 1 = — 4 ; x 2 = 2

Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.

Найти корни уравнения:

x 2 — x — 6 x — 3 = x + 2

Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:

x 2 — x — 6 \ 1 x — 3 — x \ ( x — 3 ) — 2 \ ( x — 3 ) = 0

x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0

x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0

0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0

Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:

Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.

Ответ: х — любое число, за исключением 3.

Требуется вычислить корни дробно-рационального уравнения:

5 x — 2 — 3 x + 2 = 20 x 2 — 4

На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:

5 \ ( x + 2 ) x — 2 — 3 \ ( x — 2 ) x + 2 — 20 \ 1 ( x — 2 ) ( x + 2 ) = 0

5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0

5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0

2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0

( x — 2 ) ( x + 2 ) ≠ 0

Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.

Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.

Ответ: корни отсутствуют

Нужно найти корни уравнения:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )

Начнем с определения ОДЗ:

— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0

При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )

( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )

( x — 3 ) x + x = x + 5

Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:

x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0

Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:

x 1 · x 2 = — 10 x 1 + x 2 = 3

В этом случае подходящими являются числа: -2 и 5.

Второе значение не соответствует области допустимых значений.

Источник