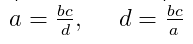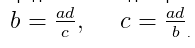Как решить пропорцию рациональным способом

Решение уравнений с пропорцией

Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию. Например, рассмотрим такое уравнение.

Для решения уравнения с пропорцией используют правило пропорции или, как его называют по-другому, правило креста.

Подробно понятие пропорции мы рассматривали в уроке «Пропорции». В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.

Правило пропорции или правило креста

Произведение крайних членов пропорции равно произведению средних.

По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции, то произведения членов пропорции, которые лежат на концах креста, равны .

Вернемся к нашему уравнению. Решим его, использую правило пропорции. Нарисуем поверх пропорции крест.

Теперь по правилу пропорции (правило креста) запишем пропорцию в виде равенства произведений крайних и средних членов пропорции.

Вспомним правило деления и решим уравнение до конца. В ответе не забудем выделить целую часть у дроби.

Рассмотрим другой пример уравнения с пропорцией.

Такое уравнение также решается с помощью правила пропорции.

Если в члене пропорции присутствуют знаки « + » или « − », обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.

Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда будете использовать правило пропорции.

После заключения в скобки члена пропорции « (2 − x) » используем правило пропорции для дальнейшего решения.

Теперь раскроем скобки с помощью правила раскрытия скобок.

Из урока «Решение линейных уравнений» используем правило переноса и правило деления для уравнений.

Не забудем при делении на отрицательное число, использовать правило знаков.

Иногда уравнения с пропорцией могут быть представлены следующим образом:

Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение, в общем для пропорции виде.

Для этого нужно вспомнить, что знак деления « : » можно заменить на дробную черту.

Источник

Задачи на пропорции

О чем эта статья:

5 класс, 7 класс, 8 класс

Понятие пропорции

Чтобы решать задачи на тему пропорции, вспомним главное определение.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.

Главное свойство пропорции:

Произведение крайних членов равно произведению средних.

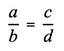
где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены.

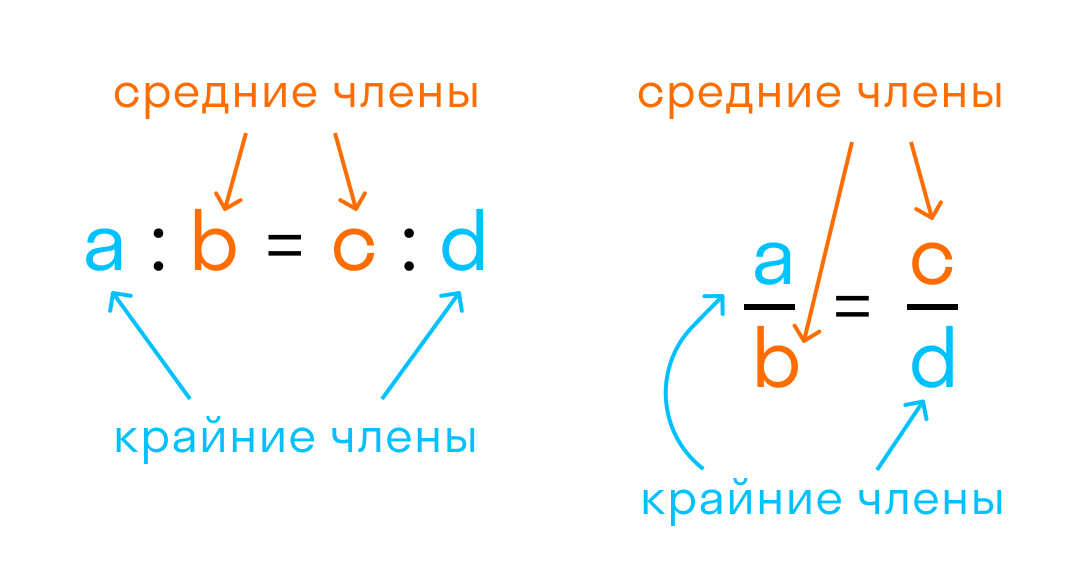
Вывод из главного свойства пропорции:

• Крайний член равен произведению средних, которые разделены на другой крайний. То есть для пропорции a/b = c/d:
  
• Средний член равен произведению крайних, которые разделены на другой средний. То есть для пропорции a/b = c/d:
  

Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.

Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.

Задачи на пропорции с решением и ответами

Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.

Задание 1. Найти неизвестный член пропорции: x/2 = 3/1

В этом примере неизвестны крайние члены, поэтому умножим средние члены и разделим полученный результат на известный крайний член:

Задание 2. Найти неизвестный член: 1/3 = 5/y

Задача 3. Решить пропорцию: 30/x = 5/8

Задание 4. Решить: 7/5 = y/10

Задание 5. Известно, что 21x = 14y. Найти отношение x — к y

Сначала сократим обе части равенства на общий множитель 7: 21x/7 = 14y/7.

Теперь разделим обе части на 3y, чтобы в левой части убрать множитель 3, а в правой части избавиться от y: 3x/3y = 2y/3y.

После сокращения отношений получилось: x/y = 2/3.

На следующем примере мы узнаем как составить пропорцию по задаче💡

Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?

Примем всех подписчиков за 100% и запишем условие задачи кратко:

Составим пропорцию: 300/108 = 100/x.

Найдем х: (108 * 100) : 300 = 36.

Ответ: 36% всех подписчиков поставили лайк под постом.

Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?

• Составим пропорцию: 5/2 = x/450.
• Найдем х: (5 * 450) : 2 = 1125.

Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.

Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?

Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.

Ответ: в 5 кг арбуза содержится 4,9 кг воды.

Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.

Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Составим пропорцию: v1/v2 = t2/t1.

Соотношения равны, но перевернуты относительно друг друга.

Подставим известные значения: 75/52 = t2/13

t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин

Ответ: 18 часов 45 минут.

Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:

Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:

Значит, 30 человек раскрутят канал за 4 дня.

Источник

Рациональные уравнения с примерами решения

Содержание:

Рациональные уравнения. Равносильные уравнения

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения — не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и — целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, — единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 — единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе — два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где — натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями — это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Источник