Как решить неравенство способом подстановки

Решение неравенств (метод подстановки).

Подстановкой в математике называется введение новой переменной. Подстановка позволяет свести решение неравенства или уравнения к двум или нескольким более простым неравенствам или уравнениям. Решая неравенство
f(x) ,,), можно сделать подстановку либо в самим неравенстве, либо при решении уравнения f(x) = 0 (третий шаг метода интервалов). Поясним это на примере. Достаточно часто, используя метод постановки, удается понизить степень уравнения или неравенства.

Пример 1. Решить неравенство х 4 — х 2 — 20.

Пусть t = х 2 . После такой подстановки получится неравенство t 2 — t — 20, которое мы решим методом интервалов.

ОДЗ: tR.

f(t) = t 2 — t — 2; эта функция непрерывна на всей области определения.

f(3) = 3 2 — 3 — 2 = 4 > 0;

Таким образом, функция f(t) = t 2 — t — 2 — t — 2 — t — 2 принимает значения небольшие 0, если -1t2. Осуществим обратный переход к переменной x, тогда -1x 2 2. Это двойное неравенство равносильно системе неравенстви, следовательно, x[-;].

Решение 2. Решим неравенство x 4 — x — 20 методом интервалов.

ОДЗ: xR.

Решим биквадратное уравнение х 4 — x 2 — 2 = 0.

Пусть t = x 2 , t 2 — t — 2 = 0, отсюда t₁ = — 1, t₂ = 2.

Производим обратный переход к переменной x.

x 2 = -1 (нет корней); x 2 = 2, x₁ = —, x₂ =.

Вычисляем значения функции f(x) = x 4 — x 2 — 2,

f(2) = 2 4 — 2 2 -2 >0;

f(0) = 04 — 02 — 2 4 — (-2) 2 — 2 >0.

Таким образом функция f(x) принимает неположительные значения на промежутке [-;].

Ответ: x[-;].

Решение 1 дает возможность свести биквадратное неравенство к квадратному
t 2 — t — 20. Далее решение этого неравенства нужно «перевести с языка t на язык х». В этом и преимущество, и недостаток решения 1. Неравенство сводится к относительно простому, но переход от х к t может вызвать затруднения. Например, если бы t = х +, то пришлось бы решать систему

Решение 2 хорошо тем, что оно дает окончательный ответ. Недостаток этого способа: при решении более сложных примеров есть опасность ошибиться в вычислениях знака функции на интервалах знакопостоянства.

Пример 2. Решить неравенство7 — x.

При решении неравенств, содержащих квадратные корни, необходимо помнить, что возведение в квадрат обеих частей неравенства, сохраняя знак неравенства, можно лишь тогда, когда обе части неравенства принимают неотрицательные значения. Если же обе части неравенства принимают неположительные значения при возведении в квадрат необходимо изменить знак неравенства на противоположный. В перечисленных случаях возможны появления посторонних решений. Возведение неравенства в квадрат в тех случаях, кода части неравенства имеют противоположные знаки, т. е. одна часть принимает неотрицательные значения, а другая неположительные значения может привести к потере решений.

Введем вспогательную переменную. Пусть t =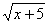, где t0, (из определения квадратного корня)
тогда t 2 = x + 5; откуда x = t 2 — 5 и имеем неравенство t7 — t 2 + 5;

t 2 + t — 120;

ОДЗ: tR.

f(t) = t 2 + t — 12; эта функция непрерывна на всей области определения. Формулу, задающую функцию, удобнее записать так f(x) = (x — 3)(x + 4).

f(4) =4 2 + 4 — 12 = 8 >0;

Таким образом, функция f(t) = t 2 + t — 12 принимает значения небольшие 0, если -4t3. Так как t0, то 0t4. Осуществим обратный переход к переменной x, тогда

03. Так как все части неравенства неотрицательны, то возведем их в квадрат 0x + 59, откуда -5x4 и, следовательно,

x[-5; 3].

Ответ: x[-5; 3].

Пример 3. Решить неравенство 2x 2 — 8x + 6 > .

В левой части неравества вынесем 2 за скобки 2 (x 2 — 4x + 3) >и введем вспомогательную переменную.

Пусть t =, тогда t > 0 и 2t 2 > t; 2t 2 — t > 0; t(2t -1) > 0.

В левой части неравенства задана квадратная функция, в которой старший коэффициент равен 1, а нули 0 и 0,5. Из свойств этой функции следует:

Таким образом неравенство 2t 2 > t равносильно неравенству t > 0,5.

Выполняем обратную замену переменных.

> 0,5, где x 3.

x 2 — 4x + 3 > 0,25;

4x 2 — 16x + 11 > 0;

D/4 = 64 — 44 = 20, D > 0.

x₁ =, x₂ =

Нетрудно установить, что 0,5 2 x — 3sinx — 2 2 — 3t — 2 2 — 42(-2) = 9 + 16 = 25, следовательно, D > 0.

3) t₁ = -0,5; t₂ = 2, поэтому решением неравенства является множество чисел
t(-; — 0,5)(2; +) (2).

Пересечение множеств (1) и (2) есть множество [-1; -0,5).

Произведем обратный переход к переменной х, получим неравенство.

-1sinx lg() + 2.

Так как -х > 0 при x lg(-x) + 2. Пусть t =, получим квадратное неравенство t 2 — 3t + 4

Источник

Решение линейных неравенств

Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.

Символ	Название	Тип знака
>	больше	строгий знак (число на границе не включается )
строгий знак (число на границе не включается )
≥	больше или равно	нестрогий знак (число на границе включается )
≤	меньше или равно	нестрогий знак (число на границе включается )

Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.

В отличии от уравнения в неравенстве вместо знака равно « = » используют любой знак сравнения: « > », « », « ≤ » или « ≥ ».

Линейным неравенством называют неравенство, в котором неизвестное стоит только в первой степени.

Рассмотрим пример линейного неравенства.

Как решить линейное неравенство

Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом « 1 ».

При решении линейных неравенств используют правило переноса и правило деления неравенства на число.

Правило переноса в неравенствах

Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот.

При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на противоположный .

Вернемся к нашему неравенству и используем правило переноса.

Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси.

Нарисуем числовую ось для неизвестного « x » и отметим на ней число « 14 ».

При нанесении числа на числовую ось соблюдаются следующие правила:

• если неравенство строгое, то число отмечается как «пустая» точка. Это означает, что число не входит в область решения;
• если неравенство нестрогое, то число отмечается как «заполненная» точка. Это означает, что число входит в область решения.

Заштрихуем на числовой оси по полученному ответу « x » все решения неравенства, то есть область слева от числа « 14 ».

Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство « x − 6 » даст верный результат.

Возьмем, например число « 12 » из заштрихованной области и подставим его вместо « x » в исходное неравенство « x − 6 ».

Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.

Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат.

Решением неравенства называют множество чисел из заштрихованной области на числовой оси.

В нашем примере ответ « x » можно понимать так: любое число из заштрихованной области (то есть любое число меньшее « 14 ») будет являться решением неравенства « x − 6 ».

Правило умножения или деления неравенства на число

Рассмотрим другое неравенство.

Используем правило переноса и перенесём все числа без неизвестного, в правую часть.

Теперь нам нужно сделать так, чтобы при неизвестном « x » стоял коэффициент « 1 ». Для этого достаточно разделить и левую, и правую часть на число « 2 ».

При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.

• Если неравенство умножается (делится) на положительное число, то
  знак самого неравенства остаётся прежним .
• Если неравенство умножается (делится) на отрицательное число, то
  знак самого неравенства меняется на противоположный .

Разделим « 2x > 16 » на « 2 ». Так как « 2 » — положительное число, знак неравенства останется прежним.

Рассмотрим другое неравенство.

Разделим неравенство на « −3 ». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.

Источник