Как решить модель задачи линейного программирования графическим способом

Решение задач линейного программирования графическим методом

Описание метода

Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.

Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1) ;
(1.2)
Здесь , есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки , так и знаки .

Построение области допустимых решений

Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.

Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой . С одной стороны от этой прямой , а с другой стороны . На самой прямой . Чтобы узнать, с какой стороны выполняется неравенство (1.2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).

Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.

Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.

Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.

Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).

Нахождение экстремума целевой функции

Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.

Теперь мы можем искать экстремум целевой функции
(1.1) .

Для этого выбираем любое число и строим прямую
(3) .
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР. На этой прямой целевая функция постоянна и равна . такая прямая называется линией уровня функции . Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение . С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение . Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .

Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.

Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.

Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.

Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений. Решением является любая точка, расположенная на отрезке между точками и , включая сами точки и .

Пример решения задачи линейного программирования графическим методом

Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида — 10 м, третьего вида — 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В — 300 ден. ед.

Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.

Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)

Тогда экономико-математическая модель задачи имеет вид:

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).

Прямые и являются осями координат.

Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

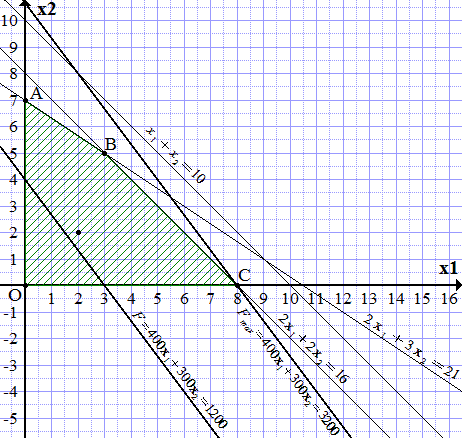
Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.

Строим произвольную линию уровня целевой функции, например,
(П1.1) .
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).

Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и . Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.

Пример 2

Решить задачу линейного программирования графическим методом.

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).

Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).

Строим прямую .
Строим прямую (ось абсцисс).

Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

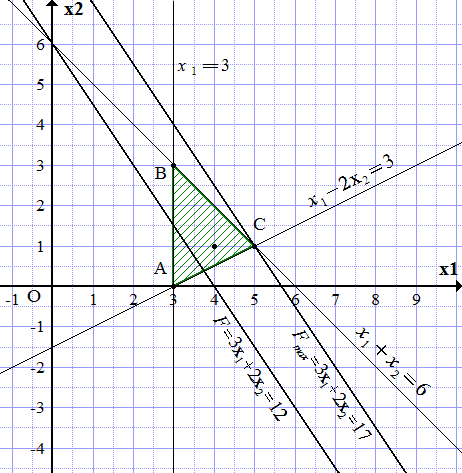
Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.

Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и , то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

Пример отсутствия решения

Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.

Решаем задачу графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).

Прямые и являются осями координат.

Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

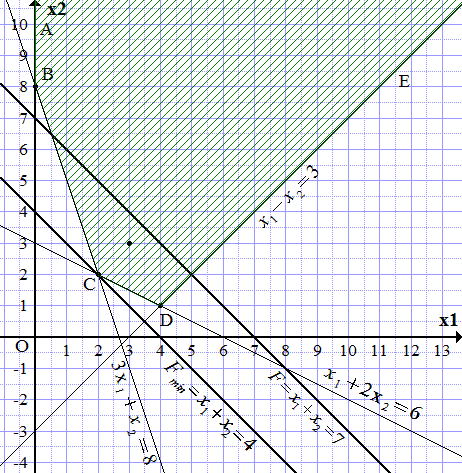
Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.

Строим произвольную линию уровня целевой функции, например,
(П3.1) .
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .

Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE. Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.

Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания , и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:

Максимального значения не существует.
Минимальное значение
.

Автор: Олег Одинцов . Опубликовано: 08-08-2016

Источник

Общая постановка задачи линейного программирования и ее графическое решение

Общая постановка задачи линейного программирования и ее графическое решение.

Задачей линейного программирования (ЗЛП) называется задача вида

где — это управляющие переменные или решения задачи,

Система неравенств (1.1.1) называется системой ограничений задачи.

Неравенства (1.1.2) – условие не отрицательности переменных.

Функция (1.1.3) – функция цели (целевая функция).

Вектор , удовлетворяющий неравенствам (1.1.1) и (1.1.2), называется планом задачи линейного программирования или допустимым вектором, или допустимым решением.

Решить задачу линейного программирования – это значит найти значения управляющих переменных , удовлетворяющих ограничениям (1.1.1) и (1.1.2), при которых це6левая функция (1.1.3) принимает минимальное или максимальное значение.

Множество всех допустимых векторов будем обозначать буквой и называть допустимым множеством или множеством планов.

Вектор называется оптимальным решением или оптимальным планом, если для всех .

Если оптимальное решение может быть найдено, то задача называется разрешимой, если же оптимального решения не существует, то задача называется неразрешимой.

Причины, по которым не может быть найдено оптимальное решение:

Функция на допустимом множестве неограниченна. Эта задача называется неразрешимой из-за неограниченности целевой функции.

Допустимое множество пусто , то есть не существует допустимых решений. Такая задача называется несовместимой.

Графический метод решения задачи линейного программирования.

Геометрически задача линейного программирования представляет собой поиск такой точки многогранника решений, координаты которой доставляют линейной функции наибольшее (наименьшее) значение, причем допустимыми решениями являются все точки многогранника решений.

Если задача линейного программирования имеет две переменные и , то ее можно решить графически.

Решение задачи происходит в два этапа.

На первом этапе необходимо на плоскости изобразить допустимое множество, а на втором найти оптимальную точку, если она существует, а в противном случае убедиться в неразрешимости задачи.

Этап 1. Построение допустимого множества.

Каждое неравенство в рассматриваемой задаче представляет собой полуплоскость, а допустимое множество – пересечение этих полуплоскостей. Если неравенства в задаче заменить уравнениями, то получим уравнения прямой. Каждую прямую можно построить по двум точкам. Для того чтобы выделить необходимую полуплоскость, надо взять точку, не лежащую на прямой, и подставить ее координаты в левую часть неравенства. Если неравенство выполнено, то выбираем полуплоскость, содержащую данную точку, в противном случае – другую полуплоскость.

Если в ограничениях присутствуют ограничения неотрицательности переменных, то рассматривается только первый координатный угол.

Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых составляют решение данной системы. Совокупность этих точек, отрезок, луч, замкнутый многоугольник, неограниченная многоугольная область.

Алгоритм выполнения первого этапа.

Шаг 1. Выделение первого координатного угла, если присутствуют ограничения неотрицательности переменных.

Шаг 3. -е неравенство записывается как уравнение.

Шаг 4. Полагаем, находим из уравнения.

Шаг 5. Полагаем, находим из уравнения.

Шаг 6. Через точку и проводится прямая.

Шаг 7. Если правая часть не равна нулю, то в качестве пробной точки удобнее всего выбрать начало координат (0,0), иначе можно взять любую точку, не лежащую на этой прямой. В левую часть неравенства подставляются координаты этой точки. Если неравенство выполнено, то выбирается полуплоскость, содержащая заданную точку, в противном случае – противоположная полуплоскость.

Шаг 8. Если , то , переходим к Шагу 3, иначе Шаг 9.

Шаг 9. Допустимое множество получено. Если оно пустое, то выписывается ответ: «Задача несовместна», иначе переход к Этапу 2.

Этап 2. Поиск оптимальной точки.

Рассмотрим градиент функции . Так как функция линейна, то ее градиент есть постоянный вектор с координатами .

Известно, что движение в направлении градиента увеличивает значение функции.

Прямая, перпендикулярная вектору-градиенту, называется линией уровня, так как значения функции в любой точке этой прямой одинаковы.

Алгоритм выполнения второго этапа.

Шаг 1. Строится вектор-градиент .

Шаг 2. Кладется линейка перпендикулярно вектору-градиенту.

Шаг 3. Линейка сдвигается параллельно самой себе по направлению вектора-градиента, пока хотя бы одна точка соответствующей прямой принадлежит допустимому множеству.

Шаг 4. Если при любом положении линейки перпендикулярно вектору-градиенту имеются точки допустимого множества, то выписывается ответ: «Задача неразрешима из-за неограниченности целевой функции» и переход к Шагу 10. Иначе Шаг 5.

Шаг 5. Находится последняя точка допустимого множества, лежащая на соответствующей линии уровня.

Шаг 6. Если эта точка не единственная, то выбирается точка, которая является пересечением двух прямых, ограничивающих допустимое множество.

Шаг 7. Выписывается система двух уравнений с двумя неизвестными.

Шаг 8. Из системы уравнений находится оптимальная точка .

Шаг 9. Находится оптимальное значение целевой функции .

При решении некоторых ЗЛП графическим методом может встретиться случай, когда линии уровня параллельна одной из сторон выпуклого многоугольника допустимых решений, причем эта сторона расположена в направлении смещения линии уровня при стремлении целевой функции к своему оптимуму. В этом случае оптимальное значение целевой функции достигается не в одной, а в двух угловых точках (вершинах) многоугольника решений и, следовательно, во всех точках отрезка, соединяющего эти вершины, то есть задача будет иметь бесчисленное множество решений.

Если область допустимых решений является незамкнутым выпуклым многоугольником в направлении оптимизации целевой функции, то целевая функция будет неограниченной и ЗЛП не будет иметь решений.

Очевидно также, что ЗЛП не будет иметь решений в случае, когда область допустимых решений есть пустое множество, то есть система ограничений ЗЛП содержит противоречивые неравенства, и на координатной плоскости нет ни одной точки, удовлетворяющей этим ограничениям.

Пример решения задачи:

Дана задача линейного программирования. Решить ее графически.

1. Построим допустимое множество решений. Для этого определим множество, как пересечение полуплоскостей всех заданных неравенств.

1) Построим прямую

Построим прямую Построим прямую

При оптимизации целевой функции на максимум крайней точкой допустимого множества является точка пересечения третей прямой с осью абсцисс. Определим эту точку:

получаем точку с координатами — это оптимальная точка.

Рассчитаем значение целевой функции в этой точке:

Источник