Как решить аналитический способ

Аналитический метод решения

При аналитическом методе решения отправляются не от условия задачи, как это делают при синтетическом методе, а от ее требования, вопроса. Это характерно для всех разновидностей аналитического метода, применяемых при решении задач.

Решение задач аналитическим методом начинается с постановки следующего вопроса, связанного с требованием решаемой задачи: «Что нужно знать, чтобы ответить на вопрос данной задачи (выполнить требование)?» Для правильного ответа на поставленный вопрос необходимо знать данные задачи и учитывать те зависимости, которые связывают их с искомым числом.

Пусть для вычисления искомого Y основной задачи требуется знать, например, числа p₁ и q₁, из которых при помощи некоторого математического действия можно получить Y, т.е. решить основную задачу. Итак, основная задача с требованием Y преобразовалась в первую серию вспомогательных задач с искомыми p₁ и q₁. Обозначим первую серию вспомогательных задач через В₁. Ставим тот же вопрос к каждой из вспомогательных задач: «Что нужно знать, чтобы найти p₁ (q₁)?» и опять при ответе на этот вопрос используем условие А основной задачи, а также арсенал математической теории.

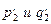
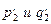
Пусть для вычисления p₁ нужно знать p₂ и q₂, а для вычисления q₁ – знать . Теперь основная задача преобразовалась во вторую серию (В₂) вспомогательных задач, включающих задачи по нахождению p₂, q₂, .

Продолжая процесс преобразования, получаем, наконец, такую серию (В_n) вспомогательных задач, искомые которых содержатся во множестве данных основной задачи.

Итак основная задача решена аналитическим методом, поскольку этим методом проведен поиск и найден путь решения задачи; главное здесь именно в этом, а не в оформлении записи уже известного решения.

Найденное аналитическое решение можно изложить различными способами, в том числе и синтетическим. В последнем случае пришлось бы следовать от конца аналитического рассуждения к его началу, не производя при этом никаких поисков.

Если основную задачу условно записать формулой А У, описанный выше аналитический путь преобразования задачи изобразится схемой:

,

Где А В_n, В_n B_n-1, . . . , В₁ У, откуда А У.

К рассмотренной в предыдущем пункте текстовой задаче применим аналитический метод решения. Наличие двух искомых в задаче несколько осложняет построение рассуждений, поэтому можно ограничиться сначала одним искомым, найти его и затем воспользоваться им как уже известным числом при отыскании пути получения второго искомого. Рассмотрим схему:

• За сколько часов может выполнить всю работу, работая отдельно, та машина, которая продолжила работу?
• Часть всей работы, выполненная этой машиной.
• Сколько часов работала эта машина отдельно когда она работала отдельно
• Объем всей работы
• Часть всей работы, выполненная двумя машинами совместно
• За сколько часов машины вместе Выполнят всю работу?
• Сколько часов они работали совместно?

Такой поиск обычно проводится устно и завершается составлением плана решения. Аналогично теперь можно построить схему аналитического поиска второго числа основной задачи (сделайте самостоятельно!).

В практике решения задач методы анализа и синтеза полностью разделить, изолировать друг от друга невозможно. Они полезно сочетаются. При аналитическом методе имеют место скрытые элементы синтеза. Например, преобразуя требование основной задачи в требования первой серии вспомогательных задач, мы неявно проверяем правильность этого преобразования, возможность синтезирования из искомых чисел задач первой серии искомого основной задачи.

Широкое применение находит аналитический метод при решении геометрических задач на вычисление. Здесь удобно начинать решение с соответствующей формулы, которая и показывает, какой будет первая серия вспомогательных задач и т.д. Кратко продемонстрируем это на примере следующей геометрической задачи.

Задача. В конус вписана пирамида, основанием которой служит прямоугольный треугольник и боковая грань которой, проходящая через один из катетов основания, образует с плоскостью основания двугранный угол α. Найти объем пирамиды, если образующая конуса равна l и наклонена к плоскости основания под углом β.

Р е ш е н и е. Начертим конус с вписанной в него пирамидой МАВС, в которой длины боковых ребер МА = МВ = МС = l, АС – гипотенуза треугольника АВС, центр основания конуса – точка О, Ао = ОС, ÐМАО=β, ÐМDО = α.

Формула объема пирамиды 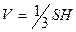. Задача сводится к нахождению площади основания S и высоты H = MO. (Первая серия из двух вспомогательных задач; последнюю из этих задач можно решить по имеющимся данным.).

Из прямоугольного треугольника ОМА находим Н = ОМ = lsinβ.

Для нахождения площади основания надо найти длины катетов АВ и ВС. (Получаем вторую серию из двух вспомогательных задач.)

Для определения АВ достаточно найти ОD – длину средней линии треугольника АВС, а для вычисления ВС надо найти АС ( третья серия из двух вспомогательных задач; решение первой задачи уже известно):

OD = MO ctgα = l sinβ ctg α.

Для получения АС достаточно знать АО ( четвертая серия – одна задача, которую можно решить):

; ; ;

;

;

.

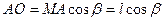
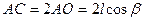
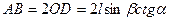
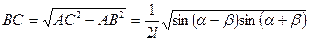
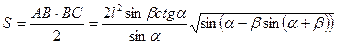
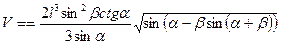
Приведенное решение является очень кратким (отсутствуют выкладки, обоснования), чтобы выделить метод решения. Учащиеся, чтобы научиться решать задачи, должны делать полные математические выкладки и уметь обосновывать каждый свой шаг в процессе решения ссылкой на условие задачи или изученную математическую теорию.

Хотя путь поиска на основе аналитического метода решения не всегда однозначен, однако он все же менее многозначен и более определен, чем путь поиска при синтетическом методе решения. Аналитический метод удобен для поиска пути решения новой для учащихся задачи, он опирается на определенное умение школьника рассуждать и эффективно способствует развитию его продуктивного, логического и функционального мышления. В результате систематического применения аналитического метода решения задач у учащихся быстрее формируется умение cамостоятельно решать новые для них задачи, чем при пользовании синтетическим методом.

Источник

Аналитические методы решения задач с параметрами

АНАЛИТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ

Проблема исследования — Традиционно задачи с параметром включаются в варианты письменных экзаменов в вузы, централизованного тестирования и Единого государственного экзамен, поэтому мною выбрана актуальная тема «Аналитические методы решения задач с параметрами».

Цель работы – систематизировать методы решения задач с параметрами, сводящихся к исследованию квадратного.

В ходе исследования решались следующие задачи –

разработать блок схемы, отображающие всевозможные варианты, возникающие при решении квадратных уравнений с параметрами.

систематизировать наиболее часто встречаемые задачи с параметрами, выделить классы задач, решаемых по единой схеме, выработать приёмы для их решения

Методика – В процессе работы изучалась, обобщалась и анализировалась теория научных работ известных математиков, таких как Г.А. Ястребинского, С.А Шестакова, Е.В Юрченко и других.

Результаты – Разработанные блок – схемы помогут учащимся решать задачи с параметрами, которые включаются в варианты предлагаемого Единого государственного экзамена, а также при подготовке к вступительным экзаменам по математике в вузы.

Аналитические методы решения задач с параметрами

Знаки корней квадратного уравнения…..………… …………..…………..…. 6

Задачи с параметрами являются наиболее трудным разделом в школьном курсе математики. Трудности решения такого рода задач вызваны прежде всего тем, что в любом случае, даже при решении простейших уравнений и неравенств ,содержащих параметры ,приходится производить ветвление всех значений параметров на отдельные классы, при каждом из которых задача имеет решение. При этом необходимо чётко следить за сохранением равносильности решаемых уравнений и неравенств с учётом области определения выражений, входящих в уравнение или неравенство.

Основной целью исследовательской работы была систематизация (в форме блок-схем)наиболее часто встречающихся и наиболее типичных задач с параметром, связанных с исследованием квадратного трехчлена. Используя блок-схемы, выполнено решение ряда заданий из сборника задач лицея ТРТУ.

Традиционно задачи с параметрами включаются в варианты письменных экзаменов в вузы, централизованного тестирования и Единого государственного экзамена.

Аналитические методы решения задач с параметрами

Определение 1 . Уравнение вида ax 2 + bx + c , где a , b , c Є R , a ≠0 , называется квадратным уравнением относительно переменной x .

Ситуации, возникающие при решении квадратных уравнений, отразим в блок-схеме I .

корня

два различных корня

Пример 1 . При каких значениях параметра c уравнение ( c -2) x 2 +2( c -2)+2=0 не имеет корней?

Решение: Рассмотрим два случая:

2) если с-2=0, с=2, то заданное уравнение примет вид 0 x 2 +0 x +2=0, 2=0, т.е.

уравнение не имеет корней.

Пример 2 . При каких значениях параметра a уравнение

(a 2 -6 a +8) x 2 +( a 2 -4) x +10-3 a — a 2 =0 имеет более двух корней?

Решение: Так как квадратное не может иметь более двух корней, а линейное может иметь бесконечно много корней, то в силу схему VI имеем

10-3a-a 2 =0 a=-5, a=2, a=2.

Пример 3 . При каких значениях параметра m уравнение

Решение: Уравнение mx 2 -( m +1) x +2 m -1=0 имеет два различных действительных корня, если D>0, m≠0.

( m +1) 2 -4(2 m -1) m >0 m 2 +2 m +1-8 m 2 +4 m >0

Знаки корней квадратного уравнения .

Всевозможные комбинации знаков корней квадратного уравнения отразим в блок-схеме II.

Корни разных знаков

Корни одного знака

Пример 1. При каких значениях параметра с уравнение

(с-1)x 2 +( c +4) x + c +7=0 имеет отрицательные корни?

Решение: Рассмотрим два случая (линейный и квадратичный):

1)если с-1=0, с=1, то уравнение примет вид 5х+8=0, х=-5/8-отрицательный корень;

2)если с-1≠0, с≠1, то следуя схеме II, получим систему:

с

1

_{-22/3 2} с

с

_{-4 1} с

-22/3≤с c ≤2 . Объединяя результаты обоих случаев, получим:

Пример 2. При каких значениях а уравнение (а-1)х 2 +2(2а+1)х+4а+3=0 имеет корни одного знака?

Рашение: Рассмотрим два случая:

1)если а-1=0, а=1, то уравнение примет вид 6х=-7, х=-7/6-один корень.

2)если а-1≠0, а≠1, то следуя схеме II:

Ответ:

Определение. Функция вида y = ax 2 + bx + c , где а≠0 , называется квадратичной. График квадратичной функции называется параболой. Абсциссы точек пересечения параболы y = ax 2 + bx + c с осью (ОХ) являются корнями уравнения ax 2 + bx + c =0 .

Отразим взаимное расположение параболы и оси (ОХ) в блок-схеме III.

Пересекает ось (ОХ)

Касается оси (ОХ)

Не пе ресекает ось (ОХ)

Лежат выше оси (ОХ)

Лежат ниже оси (ОХ)

Пример 1. При каких значениях параметра а вершина параболы

Решение: Пусть (х ₀ ; у ₀ )- координаты вершины параболы. В силу замечания имеем х ₀ =7а, у ₀ =а 2 -10 +3а. Так как вершина параболы лежит в третьей четверти, то

-5 a

Пример 2. При каких значениях параметра b график функции лежит ниже оси (ОХ) ?

Решение: Рассмотрим два случая:

1)Если b =2 , то прямая у=8х-1 не лежит ниже оси (ОХ).

2)Если . b =-2 , то прямая у=-1 лежит ниже оси (ОХ) .

2.Пусть 4-b 2 ≠0 , тогда в соответствии со схемой III получим:

Настоящая исследовательская работа «Аналитические методы решения задач с параметрами» посвящена актуальному вопросу, систематизации методов решения задач с параметрами, сводящихся к исследованию квадратного трёхчлена.

В процессе работы были разработаны блок схемы, отображающие всевозможные варианты, возникающие при решении квадратных уравнений, исследованию корней квадратных уравнений.

Разработанные блок – схемы помогут учащимся решать задачи с параметрами, которые традиционно включаются в варианты предлагаемого Единого государственного экзамена, а также при подготовке к вступительным экзаменам по математике в вузы.

В процессе работы изучалась, обобщалась и анализировалась теория научных работ известных математиков, таких как Г.А. Ястребинского, С.А Шестакова, Е.В Юрченко и других.

1. Г. А. Ястребинецкий «Задачи с параметрами» Москва: «Просвещение», 1988 год

2. С. А. Шестаков, Е. В. Юрченко «Уравнения с параметром» Москва, 1993 г

3. И. А. Кушнир «Неравенства» Киев: Астарта, 1996 г.

4. П. И. Горнштейн, В. Б. Полонский «Задачи с параметрами»

М.: Илекса, 1998 г

5. И. А. Лепская, А. Е. Лепский «Методы решения задач с параметрами», материалы II методического семинара, Таганрог: ТРТУ, 2003 г.

Источник