Как решать задачи геометрическим способом

Как решать задачи геометрическим способом

При решении геометрических задач обычно используются три основных метода: геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем; алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений; комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других — алгебраическим.

Какой бы путь решения ни был выбран, успешность его использования зависит, естественно, от знания теорем и умения их применять.

Метод дополнительного построения

Всякое геометрическое решение геометрической задачи начинается с работы над чертежом. При этом иногда на «естественном» чертеже (т.е. на чертеже, на котором изображено только условие) трудно заметить связи между данными и искомыми величинами, а если фигуру достроить, эти связи становятся очевидными.

Две фигуры F и F ₁ называются подобными, если они переводятся друг в друга преобразованием подобия, т.е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз.

Признаки подобия треугольников:

1) Если два угла одного соответственно равны двум углам другого;

2) Если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами равны;

3) Если три стороны одного треугольника пропорциональны трем сторонам другого.

Метод замены широко применяется в алгебре, но не менее эффективно «замена» может быть применена в геометрии. Сущность этого приема решения геометрических задач состоит в следующем: фигура, о которой идет речь в условии задачи, так заменяется фигурой с той же искомой величиной, чтобы найти эту величину было легче.

Метод введения вспомогательного неизвестного

Суть метода заключается в том, что исходя из условия задачи составляют уравнение (или систему уравнений). В качестве вспомогательных аргументов удобно выбирать величины, которые вместе с данными из условия задачи дают набор элементов, однозначно задающих некоторую фигуру.

В математических задачах часто бывает полезен такой прием: двумя способами найти одну и ту же величину и приравнять полученные для нее выражения. Пусть мы, например, двумя способами нашли площадь некоторой фигуры. Если в одном из выражений для площади входит, скажем синус какого-либо угла α, то при помощи соотношения из полученного равенства можно получить некоторое неравенство, порой интересное.

Метод «вспомогательных объёмов»

Для нахождения расстояния от точки до плоскости или при нахождении углов между прямой и плоскостью метод «вспомогательного объёма» во многих случаях оказывается наиболее эффективным. Суть метода заключается в том, что объём некоторой фигуры выражается двумя способами, а затем из полученных равенств выражается искомая величина. Причём в этом методе нет необходимости строить проекцию прямой на плоскость или проекцию точки, что во многих случаях оказывается очень затруднительным.

Применение критериев коллинеарности и компланарности векторов в решении задач.

Критерии коллинеарности и компланарности векторов служат основной для применения векторной алгебры в решении стереометрических задач. Они позволяют выразить в виде векторных равенств различные утверждения о расположенных точках, прямых и плоскостей в пространстве. Переход от векторных равенств к скалярным происходит на основе единственности разложения вектора по двум неколлинеарным и трём некомпланарным векторам.

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. И, решая ту или иную геометрическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще, удобнее. Некоторые виды координатных систем, отличные от прямоугольных.

1.Косоугольные (аффинные) координаты.

Рассмотрим самые употребительные и простые координаты в пространстве, называемые прямоугольными. Их называют ещё декартовыми по имени Рене Декарта (1596-1650) – французского учёного и философа, впервые ввёдшего координаты в геометрию (на плоскость).

Источник

Как решать задачи геометрическим способом

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

• Главная
• 9-Класс
• Алгебра
• Видеоурок «Геометрический способ решения текстовых задач»

Существует несколько способов решения текстовых задач:

арифметический способ – это способ решения текстовой задачи с помощью чисел и знаков арифметических действий сложения, вычитания, умножения и деления, то есть с помощью нескольких действий над числами, связанных между собой;

алгебраический способ – это способ решения текстовой задачи с помощью введения переменных и составления соответствующего уравнения или неравенства, или системы уравнений или неравенств;

геометрический способ – это способ решения текстовой задачи с помощью применения геометрических знаний;

схематический способ – это способ решения текстовой задачи с помощью схем;

графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной системе координат.

Каждый из этих способов предполагает перевод условий задачи на язык математики. Это действие математики называют математическим моделированием. Результат этого действия называют математической моделью. При применении различных способов решения получаются различные математические модели. В арифметическом способе математической моделью является числовое выражение, то есть числовой пример с несколькими действиями, а конечный результат вычислений будет решением задачи. В алгебраическом способе математической моделью чаще всего является уравнение, а решение уравнения даёт решение задачи. В геометрическом способе математической моделью является геометрическая фигура, а решение задачи – это один из найденных элементов этой фигуры. В схематическом способе математической моделью является схема, с помощью которой находят решение задачи. В графическом способе математической моделью является график, построенный по условию задачи. При этом способе решением задачи являются координаты определённых точек графиков.

На этом занятии мы рассмотрим геометрический способ решения текстовых задач.

Геометрический способ решения текстовых задач заключается в применении свойств геометрических фигур и взаимосвязи их элементов в процессе решения задачи. Этот способ делает решение текстовой задачи более наглядным и позволяет избежать громоздких вычислений. Для составления математических моделей задач геометрическим способом чаще всего применяются отрезки и их длины, а также прямоугольники и их площади. Рассмотрим следующую задачу.

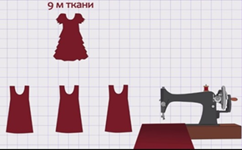
На одно платье и три сарафана пошло 9м ткани, а на три таких же платья и пять сарафанов – 19м ткани. Сколько ткани требуется на одно платье и на один сарафан?

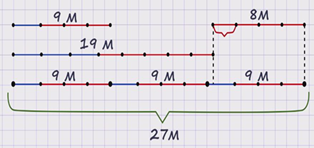
Во-первых, составим геометрическую модель этой задачи. Изобразим одно платье синим отрезком одной длины, а три сарафана – тремя синими отрезками другой длины. Все четыре отрезка будут моделировать количество ткани, использованное для пошива платья и трёх сарафанов, то есть 9м. Ниже смоделируем соответствующими отрезками условие задачи, что на три таких же платья и пять сарафанов потратили 19м ткани, значит, начертим три синих и пять красных соответствующих отрезка. Так как во втором условии задачи платьев в три раза больше, чем в первом условии, то в третьей строке начертим три фигуры первой строки, получим три синих и девять красных отрезков общей условной длиной 27м.

Получили, что длина третьей фигуры отличается от длины второй фигуры на 4 равных синих отрезка, а длина их соответствует 27 – 19метрам, то есть 8-ми метрам. Итак, получили, что на 4 сарафана потрачено 8 м ткани, значит, на один сарафан – 2м. Найти длину ткани, потраченной на платье, позволит первая фигура. Очевидно, что длина синего отрезка соответствует 9 – 3 умноженное на 2м, то есть 3м ткани. Таким образом, мы ответили на главные вопросы задачи: 3м ткани требуется на одно платье и 2м на один сарафан.

Рассмотрим другую задачу на применение геометрического метода с использованием свойств площади прямоугольника.

Токарь должен был изготовлять по 24 детали в день, чтобы выполнить задание в срок. Однако он делал в день на 15 деталей больше и уже за 6 дней до срока изготовил 21 деталь сверх плана. Сколько деталей должен был изготовить токарь?

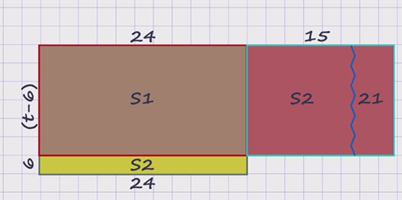
Так как в этой задаче общий объём изготовленных деталей зависит от производительности и времени работы токаря, то наиболее удобной моделью этой задачи будет прямоугольник. Одна из его сторон будет характеризовать производительность, а другая – время работы. Так как объём выполненной работы равен произведению скорости выполнения работы на время, а площадь прямоугольника равна произведению её сторон, то общее количество сделанных деталей будет отражать площадь смоделированного прямоугольника. По условию задачи токарь должен был изготовлять по 24 детали в день, чтобы выполнить задание в срок, значит, изобразим прямоугольник длиной 24условных единицы и шириной t единиц, где t – характеризует время, необходимое для выполнения задания в срок.

Однако по условию задачи токарь делал в день на 15 деталей больше и уже за 6 дней до срока изготовил 21 деталь сверх плана. Значит, смоделируем новый прямоугольник длиной большей на 15 условных единиц и шириной меньшей на 6 условных единиц и наложим для сравнения его на первоначальный прямоугольник. Таким образом, плановое выполнение деталей соответствует сумме площадей двух прямоугольников S1 + S2, а фактическое выполнение больше плана на 21 деталь, то есть S1 + S2 + 21. Из чертежа несложно определить, что S2 = 24умноженное на 6, то есть S2 = 144(деталям). Значит, площадь красного прямоугольника будет выражена 15умноженное на t – 6 с одной стороны, и 144 + 21 с другой стороны. Решая несложное уравнение 15t – 90 = 165, получаем, что t = 17. Таким образом, по плану токарь должен был затратить 17 дней. Следовательно, по плану токарь должен изготовить 17 умноженное на 24 деталей, то есть 408 деталей.

Мы рассмотрели геометрический способ. Этот способ полезен тем, что он позволяет избежать громоздких вычислений. Для успешного применения этого способа важно научиться видеть фигуры, позволяющие увязать известные и неизвестные величины из условия задачи.

Чтобы решить текстовую задачу геометрическим способом, надо

1. смоделировать условия задачи в геометрические фигуры, чаще это отрезки или прямоугольники;

2. увязать числовые данные и неизвестные искомые величины, упомянутые в условии задачи;

3. опираясь на свойство отрезков, что длина отрезка равна сумме всех его частей, на которые он разбивается любой его точкой, или на свойство площади прямоугольника, что площадь прямоугольника равна сумме площадей всех его фигур, на которые он разбит, составить числовое выражение или несложное уравнение с переменной. Значение числового выражения или решение уравнения позволят ответить на главный вопрос задачи.

Источник

Геометрический метод (подобия) решения текстовых задач (на движение, работу) в курсе математики (8-9 класс)

НЕСТАНДАРТНЫЕ МЕТОДЫ РЕШЕНИЯ ТЕКСТОВЫХ ЗАДАЧ В КУРСЕ МАТЕМАТИКИ

Умение решать текстовые задачи является одним из показателей уровня математического развития. Решение задач есть вид творческой деятельности, а поиск решения – процесс изобретательства.

В настоящее время в КИМах ЕГЭ по математике присутствуют разнообразные текстовые задачи. Среди них встречаются задачи на движение по замкнутой дороге, на движение протяженных тел, задачи на неявный объем работы, задачи на сложные проценты, на концентрацию.

В связи с этим возникла необходимость восполнить недостаток программы по математике за курс средней школы, ознакомить учащихся с разными методами решения задач, выработать у них умения и навыки решать задачи алгебраическим методом.

Решения задач на движение методом подобия.

Основное преимущество геометрического метода в его наглядности. Оно позволяет увидеть то, что в алгебраическом методе скрыто за аналитическими выкладками. Кроме того, выполненный рисунок позволяет рассуждать, делать выводы. Недаром еще великий Р. Декарт в своем труде “ Правила для руководства ума” специально выделял правило о том, что “полезно чертить… фигуры и преподносить их внешним чувствам, для того чтобы таким образом нам было легче сосредотачивать внимание нашего ума”. Особую ценность это правило имеет при решении текстовых задач.

Два пешехода вышли одновременно из двух сел А и В навстречу друг другу. После встречи первый пешеход шел 25 минут до села В, а второй шел 36 минут до села А. Сколько минут они шли до встречи?

Пусть до встречи пешеходы шли Х минут. Тогда первый был в пути (Х +25) минут, второй (Х + 36) минут. В 1 минуту первый пешеход проходил 1/(х +25)м., а второй 1/(х +36)м. расстояния АВ. Вместе они проходили в 1 минуту 1/х м. расстояния АВ. Составим уравнение:

Это уравнение имеет единственный положительный корень Х= 30. Следовательно, пешеходы шли до встречи 30 минут.

Теперь рассмотрим метод подобия, часто помогающий избежать громоздких рассуждений и составления сложного уравнения (или нескольких уравнений).

Пусть до встречи пешеходы шли Х минут. Построим графики движения пешеходов. Так как в задаче работа рассматривается как равномерный процесс, то отрезок АО – график движения первого пешехода, а отрезок ВР – график движения второго пешехода, АК – изображает время движения до встречи, МО– время движения первого пешехода после встречи до села В, МО=25,КР– время движения второго пешехода после встречи до села А, КР = 36. Проведем МК ‖ АВ и рассмотрим образовавшиеся треугольники.

Из подобия двух пар треугольников BNM и PNK, MNO и KNA (по двум углам) следует, что

Это уравнение имеет единственный положительный корень Х = 30. Следовательно, пешеходы шли до встречи 30 минут.

Из двух городов навстречу друг другу вышли одновременно два курьера. После встречи один был в пути 16 часов, а другой – 9 часов. Сколько времени был в пути каждый?

Можно составить систему из двух уравнений с тремя неизвестными, которая сводится к квадратному уравнению, дающему ответ t ₁ = 21, t ₂ = 28.

А мы условие задачи представим графически, смотри рис. 3.

Аналогично решению предыдущей задачи из подобия треугольников имеем ; t 2 =144; t = 12.

12 +6 =28(Ч), 12 + 9 =21(ч).

Ответ: 21 ч, 28 ч.

Три пункта – А, В, С – расположены на одной прямой, причем пункт В расположен между А и С. Из пунктов А и В по направлению к С одновременно выехали две машины. Через 5 часов расстояние между ними составило треть расстояния ВС, а еще через 5 часов они одновременно прибыли в С. Найдите отношение скоростей автомобилей.

Сразу рисуем графики, соответствующие условию данной задачи (рис. 4) и начинаем размышлять.

Из пункта А в пункт В вышел пешеход. Вслед за ним через 2 ч из пункта А выехал велосипедист, а еще через 30 мин – мотоциклист. Пешеход, велосипедист и мотоциклист двигались равномерно и без остановок. Через некоторое время после выезда мотоциклиста оказалось, что к этому моменту времени все трое преодолели одинаковую часть пути от А до В. На сколько минут раньше пешехода в пункт В прибыл велосипедист, если пешеход прибыл в пункт В на 1 ч позже мотоциклиста?

Для алгебраического решения задачи ситуация, описанная в ней, требует введения целого ряда неизвестных и составления системы из нескольких уравнений. В целях экономии времени не будем решать задачу с помощью системы. Итак, рассмотрим решение этой задачи геометрическим методом. Ситуацию, описанную в задаче, изобразим графически.

Поскольку все движения равномерные, то условию задачи соответствует рисунок 2.

А теперь, как говорили древние математики– индусы, “Смотри!”:

Из подобия треугольников (опустим доказательство ) следует пропорция

Ответ: на 48 мин.

Вывод: Благодаря интеграции алгебраического и геометрического методов, математические знания предстают перед вами как “живая”, динамическая система, способная решать любые задачи.

Некоторые задачи на работу аналогичны задачам на движение. Давайте попробуем применить описанный способ к решению такой задачи.

Решения задач на работу методом подобия.

Чан наполняется водой при помощи двух кранов А и В. Наполнение чана только с помощью крана А длится на 22 минуты дольше, чем наполнение через кран В. Если же оба крана открыть одновременно, то чан наполнится водой за 1 час. За какое время может наполнить водой чан только кран В?

Рассмотрим рисунок. На нем АА1 и BВ1 – графики зависимости выполненного объема работы от времени наполнения чанов водой кранами А и В соответственно.

По условию задачи ВК = АN = 1 час = 60 минут. В1М = 22 минуты. Используем подобие треугольников:

ΔBКО подобен ΔВ1NO, тогда BK/NB1 = KO/ON; 60/x = KO/ON.

Δ KOA1 подобен Δ NOA, тогда KA1/AN = KO/ON; (x + 22)/60 = KO/ON.

Таким образом, имеем пропорцию 60/x = (x + 22)/60.

Перепишем в виде квадратного уравнения:

х 2 + 22х – 3600 = 0;

х = 50 или х = -72.

По смыслу задачи х = 50 минут.

Таким образом, АВ1 = AN + NВ1 = 60 + 50 = 110 (минут).

Ответ: 110 минут.

Двое рабочих, выполняя задание вместе, могли бы закончить его за 12 дней. Если сначала будет работать только один из них, а когда он выполнит половину всей работы, его сменит второй рабочий, то все задание будет закончено за 38 дней. За сколько дней каждый рабочий в отдельности может выполнить все задание?

Алгебраический метод решения приводит к уравнению

Где Х– количество дней, за которое первый рабочий выполнит все задание.

2 способ. Теперь рассмотрим метод подобия.

Построим графическую модель задачи (рис. 5).

Для определенности предположим, что первый рабочий работает быстрее, чем второй. Так как в задаче работа рассматривается как равномерный процесс, то отрезок AN – график работы первого рабочего, а отрезок BD – график работы второго рабочего, AQ изображает время совместной работы, AQ = 12. Проведем NK ІІ BD, тогда AK = 50. Далее используем подобие образовавшихся треугольников.

Треугольники NMA, PQA и PCN подобны по двум углам, отсюда следует, что

Треугольники NMK, PQD и PCB подобны по двум углам, отсюда следует, что

Составим уравнение: . Решая это уравнение, находим: х ₁ =18, х ₂ = 8. Учитывая, что первый рабочий работает быстрее, то Х ₁ , его изображает отрезок AM, равно 20 ч, а время t ₂ , его изображает отрезок MK,равно 30 ч.

Ответ: 20 ч, 30 ч.

Задание 1 . Двое рабочих, выполняя некоторое задание вместе, могли бы справиться с ним за 12 дней. Если сначала будет работать только один из них, а когда он выполнит половину всей работы, его сменит второй рабочий, то все задание будет выполнено за 25 дней. За какой срок, работая один, второй рабочий сможет выполнить все задание?

Источник