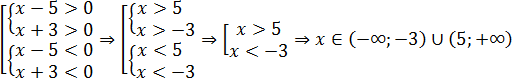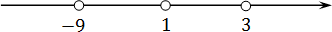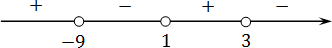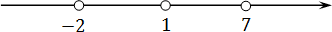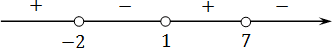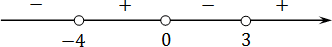- Метод интервалов: решение простейших строгих неравенств
- Почему эти методы неэффективны?
- Замечание по поводу знаков функции
- Квадратные неравенства. Метод интервалов
- Как решить квадратное неравенство
- Что такое метод интервалов
- Краткая запись решения методом интервалов
- Другие примеры решения квадратных неравенств
Метод интервалов: решение простейших строгих неравенств
Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 x + 3
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
x 2 − 2 x − 15 > 0
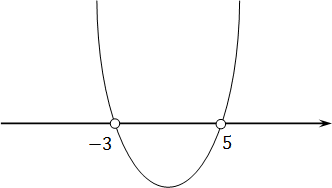
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:
Функция больше нуля там, где она проходит выше оси OX . В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
( x − 7)( x − 1)( x + 4)( x + 9) f ( x ) > 0 и f ( x ) f ( x ) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f ( x ) > 0, или знаком «−», если неравенство имеет вид f ( x ) x − 2)( x + 7) x − 2)( x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f ( x ) = ( x − 2)( x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f (3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
Вернемся к исходному неравенству, которое имело вид:
( x − 2)( x + 7) x + 9)( x − 3)(1 − x ) x + 9)( x − 3)(1 − x ) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f ( x ) = ( x + 9)( x − 3)(1 − x );
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
( x + 9)( x − 3)(1 − x ) f ( x ) x ∈ (−9; 1) ∪ (3; +∞)
Это и есть ответ.
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
- Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f ( x ) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
- Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид ( a ; +∞), где a — самый большой корень уравнения f ( x ) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:
( x − 1)(2 + x )(7 − x ) f ( x ) = ( x − 1)(2 + x )(7 − x );
( x − 1)(2 + x )(7 − x ) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
Требуется найти знак функции f ( x ) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f ( x ) = −1 и f ( x ) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f ( x ) = ( x − 1)(2 + x )(7 − x )
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: ( x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x ). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x ). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
Исходное неравенство имело вид:
( x − 1)(2 + x )(7 − x ) x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Заменяем неравенство уравнением и решаем его:
x (2 x + 8)( x − 3) = 0;
x = 0;
2 x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f ( x ) = x (2 x + 8)( x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
Источник
Квадратные неравенства.
Метод интервалов
Прежде чем разбираться, как решать квадратное неравенство, давайте рассмотрим, какое неравенство называют квадратным.
Неравенство называют квадратным, если старшая (наибольшая) степень неизвестного « x » равна двум.
Потренируемся определять тип неравенства на примерах.
| Неравенство | Тип |
|---|---|
| x − 7 2 + 5x ≥ 0 | квадратное |
| 2x − 7 > 5 | линейное |
| x 2 + x − 12 ≤ 0 | квадратное |
Как решить квадратное неравенство
В предыдущих уроках мы разбирали, как решать линейные неравенства. Но в отличие от линейных неравенств квадратные решаются совсем иным образом.
Решать квадратное неравенство таким же образом как и линейное нельзя !
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Что такое метод интервалов
Методом интервалов называют специальный способ решения квадратных неравенств. Ниже мы объясним, как использовать этот метод и почему он получил такое название.
Чтобы решить квадратное неравенство методом интервалов нужно:
- перенести все члены неравенства в левую часть, так чтобы в правой остался только ноль;
- сделать так, чтобы при неизвестном « x 2 » стоял положительный коэффициент;
- приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение;
- полученные корни уравнения разместить на числовой оси в порядке возрастания;
- нарисовать «арки» для интервалов. Справа налево, начиная с « + », проставить чередуя знаки « + » и « − »;
- выбрать необходимые интервалы и записать их в ответ.
Мы понимаем, что правила, описанные выше, трудно воспринимать только в теории, поэтому сразу рассмотрим пример решения квадратного неравенства по алгоритму выше.
Требуется решить квадратное неравенство.
Переходим к п.2. Необходимо сделать так, чтобы перед « x 2 » стоял положительный коэффициент. В неравенстве « x 2 + x − 12 » при « x 2 » стоит положительный коэффициент « 1 », значит, снова нам ничего делать не требуется.
Согласно п.3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
x1;2 =
| −1 ± √ 1 2 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
| −1 ± √ 1 + 48 |
| 2 |
x1;2 =
| −1 ± √ 49 |
| 2 |
x1;2 =
| −1 ± 7 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = −4 | x2 = 3 |
Теперь по п.4 отметим полученные корни на числовой оси в порядке возрастания.
Помните, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси разным образом.
Теперь, как сказано в п.5, нарисуем «арки» над интервалами между отмеченными точками.
Проставим знаки внутри интервалов. Справа налево чередуя, начиная с « + », отметим знаки.
Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ. Вернемся к нашему неравенству.
Так как в нашем неравенстве , значит, нам требуются отрицательные интервалы. Заштрихуем все отрицательные области на числовой оси и выпишем их в ответ.
Отрицательным интервалом оказался лишь один, который находится между числами « −4 » и « 3 », поэтому запишем его в ответ в виде двойного неравенства
−4 .
Запишем полученный ответ квадратного неравенства.
Именно из-за того, что при решении квадратного неравенства мы рассматриваем интервалы между числами, метод интервалов и получил свое название.
После получения ответа имеет смысл сделать его проверку, чтобы убедиться в правильности решения.
Выберем любое число, которое находится в заштрихованной области полученного ответа −4 и подставим его вместо « x » в исходное неравенство. Если мы получим верное неравенство, значит мы нашли ответ квадратного неравенства верно.
Возьмем, например, из интервала число « 0 ». Подставим его в исходное неравенство « x 2 + x − 12 ».
Мы получили верное неравенство при подстановке числа из области решений, значит ответ найден правильно.
Краткая запись решения методом интервалов
Сокращенно запись решения квадратного неравенства методом интервалов будет выглядеть так:
x 2 + x − 12 2 + x − 12 = 0
x1;2 =
| −1 ± √ 1 2 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
| −1 ± √ 1 + 48 |
| 2 |
x1;2 =
| −1 ± √ 49 |
| 2 |
x1;2 =
| −1 ± 7 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = −4 | x2 = 3 |

Другие примеры решения квадратных неравенств
Рассмотрим решение других примеров квадратных неравенств. Требуется решить квадратное неравенство:
В правой части неравенство уже стоит ноль. При « x 2 » стоит « 2 » ( положительный коэффициент), значит можно сразу переходить к поиску корней.
x1;2 =
| −(−1) ± √ (−1 2 ) − 4 · 2 · 0 |
| 2 · 2 |
x1;2 =
| 1 ± √ 1 |
| 4 |
x1;2 =
| 1 ± 1 |
| 4 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
x1 =
| x2 = 0 |

| 1 |
| 2 |
Рассмотрим пример, где перед « x 2 » в квадратном неравенстве стоит отрицательный коэффициент.
По п.2 общих правил решения методом интервалов нам нужно сделать так, чтобы перед « x 2 » стоял положительный коэффициент. Для этого умножим все неравенство на « −1 ».
Помните, что при умножении неравенства на отрицательное число, знак неравенства меняется на противоположный .
Можно переходить к п.4 и п.5. Приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение. Затем расположим полученные корни на числовой оси и проведем между ними «арки».
x1;2 =
| −3 ± √ 3 2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
| −3 ± √ 9 + 16 |
| 2 |
x1;2 =
| −3 ± √ 25 |
| 2 |
x1;2 =
| −3 ± 5 |
| 2 |
x2 =
| x1 =
| ||||
x2 =
| x1 =
| ||||
| x2 = −4 | x1 = 1 |

При определении того какие интервалы нам нужно брать в ответ, исходить нужно из самого последнего изменения неравенства перед нахождением его корней.
В нашем случае самая последняя версия неравенства перед поиском корней уравнения это « x 2 + 3x − 4 ≤ 0 ».
Значит для ответа нужно выбирать интервалы со знаком « − ».

К сожалению, при решении квадратного неравенства не всегда получаются два корня и все идет по общему плану выше. Возможны случаи, когда получается один корень или даже ни одного корня.
Как решить квадратные неравенства в таких случаях, мы разберем в следующем уроке «Квадратные неравенства с одним корнем или без корней».
Источник