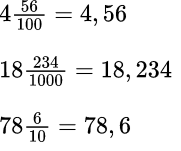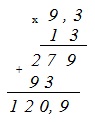Как решать удобным способом десятичные дроби

Десятичные дроби

теория по математике 📈 числа и вычисления

Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).

Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:

4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых

Чтение десятичных дробей

Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).

Десятичные дроби получаются из обыкновенных дробей:

Сложение (вычитание) десятичных дробей

Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:

1. Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
2. Уравнять количество знаков после запятой, добавляя недостающие нулями.
3. Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
4. Поставить запятую под запятыми.

Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.

Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.

34,145 + 5,678 = 39,823

34,145 5,678 39,823

Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.

9,235 – 2,34 = 6,895

Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.

Умножение десятичных дробей

При умножении двух десятичных дробей в столбик необходимо:

1. Написать числа одно под другим, не обращая внимания на запятую
2. Выполнить умножение в столбик
3. В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.

Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.

0,125 × 2,3 00375 0250 0,2875

Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.

Умножение десятичных дробей на 10, 100, 1000…

Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.

Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.

Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.

Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.

Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…

При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.

Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.

Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.

Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.

Деление десятичных дробей

1. При делении десятичной дроби на целое число выполняют сначала деление целой части, а затем десятичной.
2. При делении десятичной дроби на другую десятичную дробь необходимо в делителе убрать запятую, а в делимом передвинуть ее вправо на столько цифр, сколько их в делителе после запятой. Затем выполнить деление на целое число.
3. Есть случаи, когда цифр после запятой при переносе запятой у дроби не хватает. Тогда необходимо дополнить число нулями.

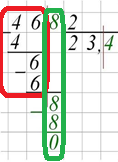
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4

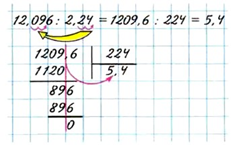
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.

Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.

Деление десятичной дроби на 10, 100, 1000…

При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.

Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.

Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.

Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…

При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.

Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.

Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.

На координатной прямой точки А, В, С и D соответствуют числам -0,201; -0,012; -0,304; 0,021.

Какой точке соответствует число -0,304?

1) А 2) В 3) С 4) D

Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.

Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304

pазбирался: Даниил Романович | обсудить разбор | оценить

–0,3·(–10) 4 +4·(–10) 2 –59

Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.

Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:

Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:

Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:

Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:

pазбирался: Даниил Романович | обсудить разбор | оценить

Это задание требует простого умения выполнять арифметические действия с десятичными дробями.

Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:

Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:

Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:

pазбирался: Даниил Романович | обсудить разбор | оценить

Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.

Вычислим значение знаменателя:

Можно произвести вычисления в столбик, тогда получим:

Либо перевести дробь к простому виду:

4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4

Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:

9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )

9 и 45 можно сократить на 9:

( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

Повторение курса

1. Десятичная дробь – это форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д.

Например, 1/100 = 0,01; 7/10 = 0,7 ; 19/1000 = 0,019

2. Запятая в десятичной дроби отделяет:

— целую часть от дробной;

— столько знаков, сколько нулей в знаменателе обыкновенной дроби.

3. Как перевести десятичную дробь в обыкновенную?

Запишите в числитель все число без запятой, а в знаменатель – единицу и столько нулей, столько цифр было отделено запятой в десятичной дроби.

4. Как обыкновенную дробь перевести в десятичную?

1 способ (хорошо работает, когда в знаменателе дроби: 2, 5, 20, 25… и т. д., то есть когда сразу понятно, на что надо умножать): домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получилось 10, 100, 1000 и т.д., а потом записать результат в десятичном виде.

2 способ: поделить числитель обыкновенной дроби на ее знаменатель (см. раздел сайта: 5 класс/десятичные дроби).

5. Сложение и вычитание десятичных дробей:

Сложение (вычитание) десятичных дробей выполняется так же, как сложение (вычитание) натуральных чисел, в столбик: главное, чтобы запятая во втором числе стояла под запятой в первом. Например:

6. Умножение десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/умножение десятичных дробей):

Чтобы перемножить две десятичные дроби, нужно умножить их как обычные числа, не обращая внимания на запятые. Потом сложить количество знаков после запятой в первом множителе и во втором множителе, а затем отделить полученное количество знаков в произведении, считая справа налево. Например:

7. Деление десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/деление десятичных дробей):

Чтобы разделить десятичную дробь на десятичную дробь, надо перенести запятую в делителе вправо на столько позиций, пока он не станет целым. Потом на столько же позиций перенести запятую в делимом. Затем разделить получившиеся числа как обычно, в столбик. При этом в ответе нужно будет не забыть поставить запятую сразу же, как мы «перейдем за запятую» в делимом. Например:

1. Вычислите:

30,75 + 5,6136 21,6 — 13,823 7,05 * 0,0308 15,6672 : 3,84

5,52 + 994,48 406,01 — 75,997 507,8 * 3,005 0,03729 : 6,78

2. Найдите значение выражения:

а) (12 — 8,4) : 0,09 * 0,7 — 0,3 * (0,6 + 3,12) : (14,18 — 7,98) : 0,01

б) 10 * (0,056 : 0,8 * 700 — 40,2832) : (16 * 0,6 — 0 : 3,2) + 5,4 : 9 : 30

3. В летнем лагере за смену в 28 дней израсходовали 1 т картофеля. В первые 12 дней расход картофеля составил 38 кг в день. Каким будет расход картофеля в оставшиеся дни, если каждый день он будет одинаковым?

4. Найдите истинные высказывания. Расположите соответствующие им ответы в порядке возрастания, сопоставив их соответствующим буквам, и расшифруйте астрономический термин. Примеры, в которых допущена ошибка, решите правильно и запишите их в тетрадь.

Р 0,4 + 3 = 3,4 Д 9,1 — 1,05 = 8,05 А 0,8 * 0,04 = 0,032

У 6 + 0,12 = 0,18 Г 0,854 — 0,85 = 0,04 К 5 : 1000 = 0,05

Н 0,25 + 0,5 = 0,3 Б 0,5 * 3 = 0,15 Т 3,6 : 9 = 0,4

О 3,28 + 1,3 = 4,58 И 4 * 1,7 = 6,8 Я 12,3 : 5 = 24,6

Е 2,6 — 0,01 = 2,59 Ж 17,2 * 10 = 1,72 С 0,056 : 0,7 = 0,08

5. У дачника было три улья. С первого улья он получил 24,8 кг мёда, со второго — на 6,4 кг меньше, чем с первого, а с третьего — половину того, что собрал с первых двух ульев вместе. Весь мёд он разложил поровну в 18 банок. По скольку килограммов мёда было в каждой банке?

6. Существует версия, что «золотое руно», за которым отправились аргонавты в Колхиду, есть не что иное, как секрет выделки одного растения. Его-то и продавали на вес золота в Древнем мире. Голубой венчик этого растения — это «цвет неба», — считали жрецы Исиды и носили одежды только из этого растения. Что это за растение? Чтобы ответить на этот вопрос, вычислите рационально:

18,7 * 3,6 — 3,6 * 8,7 + 4,4

17,3 * 18,9 — 18,9 * 3,1 + 15,8 * 18,9

37,2 * 18,2 — 18,2 * 21,3 + 19,2 * 15,9 + 15,9 * 2,6

Е=40,4 ; Д=36 ; С=8 ; Н=567 ; У=684,18 ; Л=636 ; Б=728 ; И=872.

7. Соком этого растения был отравлен король датский, отец Гамлета. Сейчас оно входит в состав мазей для лечения простуды, бронхита, плеврита, т. к. вещества, входящие в его состав, оказывают спазмолитическое действие. Что это за растение? (Результат каждого действия даёт букву.)

227,36 : (865,6 — 20,8 * 40,5) * 8,38 + 1,12 — 44

А=842,4 ; К=844,2 ; Е=23,2; С=93,5 ; Е=9,8 ; О=84,24 ; Н=82,124 ; Б=83,244 ; Л=39,244 ; Я=83,2.

8. Этого симпатичного зверька на латыни именовали «королём зелени». Назовите его:

(68,344 — 3,09 : 1,5) : 7,3 + 2,7 * 8,5 — 2,03

Б=26 ; О=2,06 ; В=2,6 ; И=66,284 ; А=681,38 ; Л=9,08 ; А=9,8 ; Ц=98 ; Н=229,5 ; Е=0,3203 ; Р=22,95 ; К=32,03 ; К=30.

9. Выполните действия и округлите полученный результат с точностью:

• до десятков: 2987,4 + 7,85; 100,1 — 47,907; 39,5 * 5,09; 163,846 : 0,79
• до единиц: 82,435 + 7,0684; 203 — 75,48; 470,5 * 0,804; 0,43236 : 0,045;
• до десятых: 205,038 + 9,47; 4,2 — 1,517; 320 * 0,0564; 0,06111 : 0,063;
• до сотых: 1,514 + 0,4872; 5,1002 — 0,005; 5,7 * 0,053; 0,649636 : 0,806

Источник