Как решать системы неравенств с двумя переменными графическим способом

Системы неравенств с двумя переменными

п.1. Алгоритм графического решения системы неравенств с двумя переменными

Найти на координатной плоскости множество решений системы неравенств: $$ \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. $$ Множество решений – сегмент круга, отсекаемый отрезком AB. Сам отрезок в множество решений не входит.

п.2. Примеры

Пример 1. Найдите на координатной плоскости множество решений системы неравенств.

Выразим y(x) в явном виде

Строим прямые, заштриховываем области над ними, находим пересечение.

Выразим y(x) в явном виде

Заштриховываем область под первой параболой и над второй параболой.

Выразим y(x) в явном виде

Строим гиперболу и прямую. Заштриховываем области под гиперболой и над прямой.

Заштриховываем области вне первой окружности и внутри второй.

Находим пересечение – кольцо.

Пример 2. Задайте системой неравенств треугольник с вершинами
A(2; 3), B(4; 4), C(3; 0)
Уравнения прямых, на которых лежат стороны треугольника:

Источник

Графическое решение неравенств, системы совокупностей неравенств с двумя переменными

Пусть f(x,y) и g(x, y) – два выражения с переменными х и у и областью определения Х. Тогда неравенства вида f(x, y) > g(x, y) или f(x, y) g(x, y), поступают следующим образом. Сначала заменяют знак неравенства знаком равенства и находят линию, имеющую уравнение f(x,y) = g(x,y). Эта линия делит плоскость на несколько частей. После этого достаточно взять в каждой части по одной точке и проверить, выполняется ли в этой точке неравенство f(x, y) > g(x, y). Если оно выполняется в этой точке, то оно будет выполняться и во всей части, где лежит эта точка. Объединяя такие части, получаем множество решений.

Задача. Решить графически неравенство y > x.

Решение. Сначала заменим знак неравенства знаком равенства и построим в прямоугольной системе координат линию, имеющую уравнение y = x.

Эта линия делит плоскость на две части. После этого возьмем в каждой части по одной точке и проверим, выполняется ли в этой точке неравенство y > x.

Задача. Решить графически неравенство
х2 + у2 £ 25.

Решение. Сначала заменим знак неравенства знаком равенства и проведем линию х2 + у2 = 25. Это окружность с центром в начале координат и радиусом 5. Полученная окружность делит плоскость на две части. Проверяя выполнимость неравенства х2 + у2 £ 25 в каждой части, получаем, что графиком является множество точек окружности и части плоскости внутри окружности.

Системы совокупностей неравенств с двумя переменными

Система неравенств представляет собой конъюнкцию этих неравенств. Решением системы является всякое значение (x, y), которое обращает каждое из неравенств в истинное числовое неравенство. Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих данную систему.

Совокупность неравенств представляет собой дизъюнкцию этих неравенств. Решением совокупности является всякое значение (x, y), которое обращает в истинное числовое неравенство хотя бы одно из неравенств совокупности. Множество решений совокупности есть объединение множеств решений неравенств, образующих совокупность.

Задача. Решить графически систему неравенств

Решение. Сначала заменяем знак неравенства знаком равенства и проводим в одной системе координат линии у = х и х2 + у2 = 25. Решаем каждое неравенство системы.

Графиком системы будет множество точек плоскости, являющихся пересечением (двойная штриховка) множеств решений первого и второго неравенств.

Задача. Решить графически совокупность неравенств

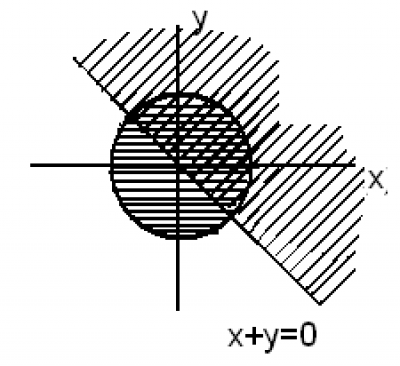
Решение. Сначала заменяем знак неравенства знаком равенства и проводим в одной системе координат линии у = х + 4 и х2 + у2 = 16. Решаем каждое неравенство совокупности. Графиком совокупности будет множество точек плоскости, являющихся объединением множеств решений первого и второго неравенств.

Упражнения для самостоятельной работы

1. Решите графически неравенства: а) у > 2x; б) у 9; г) x2 + y2 £ 4.

2. Решите графически системы неравенств:

а) в)

б) г)

3. Решите графически совокупности неравенств:

а) в)

б) г)

Источник

Линейные неравенства с двумя переменными и их системы

Линейное неравенство с двумя переменными и его решение

Неравенство вида ax+by $ \begin \lt \\ \gt \\ \le \\ \ge \end $ c , где a, b, c — данные числа, называется линейным неравенством с двумя переменными x и y.

Например: $2x+5y \lt 6; -x+1, 5y \ge 0; \frac<1> <2>x-8y \gt 7$

Решением неравенства с двумя переменными называется упорядоченная пара значений переменных (x,y), обращающая это неравенство в истинное выражение.

Например: для неравенства $2x+5y \lt 6$

пара (-1;-2) является решением, т.к. $2\cdot(-1)+5 \cdot (-2) = -12 \lt 6$ – истина

пара (1;2) не является решением, т.к. $2\cdot1+5\cdot2=12 \not\lt 6$ – ложь

Графическое представление линейного неравенства с двумя переменными

Графическим представлением линейного неравенства с двумя переменными вида ax+by$ \begin \lt \\ \gt \\ \le \\ \ge \end $ c является полуплоскость с границей ax+by = c .

Для строгого неравенства граница не входит в представление, для нестрогого неравенства – входит.

Графическое решение системы линейных неравенств с двумя переменными

Графическим решением системы линейных неравенств с двумя переменными является пересечение их графических представлений на плоскости.

Пересечение двух множеств – это множество, которому принадлежат только те элементы, которые одновременно входят в оба множества.

Пересечение обозначают знаком $\cap$.

Найдём графическое решение системы линейных неравенств:

Решением является треугольник ABC, где A(-1;2), B(0;4), C(2;0).

Примеры

Пример 1. Найдите графическое представление линейного неравенства:

Представление – полуплоскость под границей, сама граница не входит

Представление – полуплоскость под границей, сама граница входит

Представление – полуплоскость справа от границы, сама граница входит

Представление – полуплоскость под границей, сама граница не входит

Пример 2*. Найдите графическое решение системы линейных неравенств:

Решением является квадрат ABCD, где A(-3;-1), B(0;2), C(3;1), D(0;-4)

Пример 3*. Автоперевозчику поступил заказ на перевозку 30 т груза. У него есть 5 машин грузоподъёмностью 3 т и 5 машин грузоподъёмностью 5 т.

Расход топлива для каждого типа грузовиков соответственно 20 и 24 л, общий расход не должен превышать 170 л.

Подберите состав грузовиков для выполнения заказа.

Пусть x — количество грузовиков по 3т, y – по 5т.

По условию задачи:

$$ <\left\< \begin 3x+5y \ge 30 \\ 20x+24y \le 170 \\ x \le 5 \\ y \le 5 \end \right.> $$

Решением системы неравенств является заштрихованный треугольник. Единственным целочисленным решением является точка A(2;5) Таким образом, для выполнения заказа нужно 2 грузовика по 3т и 5 грузовиков по 5т.

Их суммарная грузоподъёмность: $3 \cdot 2+5 \cdot 5 = 31 \gt 30$ достаточна

Суммарный расход топлива: $ 20 \cdot 2+24 \cdot 5 = 160 \lt 170 $ не превышает лимит

Ответ: 2 грузовика по 3т и 5 грузовиков по 5т

Источник

Как решать системы неравенств с двумя переменными графическим способом

• Главная
• Обучение
• Предварительный просмотр

• Мероприятия / ВИШР
• Обучение
• Тренажер ЕГЭ
• Учебные пособия
• Игры
• 120 лет ТПУ. Викторина онлайн
• Университетские субботы
• Высшая инженерная школа России

Математика

2.2.10. Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем

Графическое решение неравенства с двумя переменными

Часто приходится изображать на координатной плоскости мно­жество решений неравенства с двумя переменными. Решением неравенства с двумя переменными называют пару значений этих переменных, которая обращает данное неравенство в верное числовое неравенство.

Изобразим на координатной плоскости множество решений нера­венства 2у + Зх 2 + 2х + у 2 — 4у + 1 > 0 на координатной плоскости.

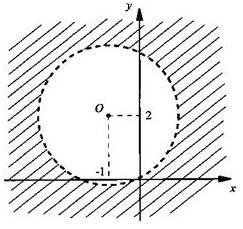
Построим сначала график уравнения х 2 + 2х + у 2 — 4у + 1 = 0. Вы­делим в этом уравнении уравнение окружности: (х 2 + 2х + 1) + (у 2 — 4у + 4) = 4, или (х + 1) 2 + (у — 2) 2 = 2 2 .

Это уравнение окружности с центром в точке 0 (-1; 2) и радиусом R = 2. Построим эту окружность.

Так как данное неравенство строгое и точки, лежащие на самой окружности, неравенству не удовлетворяют, то строим окружность пунктирной линией.

Легко проверить, что координаты центра О окружности данному неравенству не удовлетворяют. Выражение х 2 + 2х + у 2 — 4у + 1 ме­няет свой знак на построенной окружности. Тогда неравенству удовлетворяют точки, расположенные вне окружности. Эти точки заштрихованы.

Пример

Изобразим на координатной плоскости множество решений нера­венства

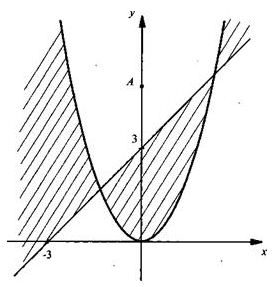
(у — х 2 )(у — х — 3) 2 )(у — х — 3) = 0. Им яв­ляется парабола у = х 2 и прямая у = х + 3. Построим эти линии и отметим, что изменение знака выражения (у — х 2 )(у — х — 3) проис­ходит только на этих линиях. Для точки А (0; 5) определим знак это­го выражения: (5- 3) > 0 (т. е. данное неравенство не выполняется). Теперь легко отметить множество точек, для кото­рых данное неравенство выполнено (эти области заштрихованы).

Алгоритм решения неравенств с двумя переменными

1. Приведем неравенство к виду f (х; у) 0; f (х; у) ≤ 0; f (х; у) ≥ 0;)

2. Записываем равенство f (х; у) = 0

3. Распознаем графики, записанные в левой части.

4. Строим эти графики. Если неравенство строгое (f (х; у) 0), то — штрихами, если неравенство нестрогое (f (х; у) ≤ 0 или f (х; у) ≥ 0), то — сплошной линией.

5. Определяем, на сколько частей графики разбили координатную плоскость

6. Выбираем в одной из этих частей контрольную точку. Определяем знак выражения f (х; у)

7. Расставляем знаки в других частях плоскости с учетом чередования (как по методу интервалов)

8. Выбираем нужные нам части в соответствии со знаком неравенства, которое мы решаем, и наносим штриховку

Источник

Читайте также:  Гексикон свечи инструкция способ применения