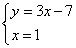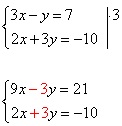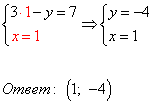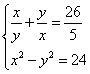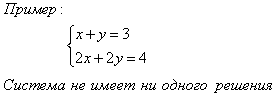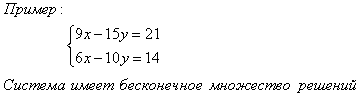Как решать систему неравенства способом подстановки

Математика

Тестирование онлайн

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену 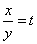, тогда

Переходим к первоначальным переменным

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если 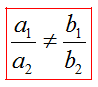, то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Метод Гаусса*

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

Источник

Решение неравенств (метод подстановки).

Подстановкой в математике называется введение новой переменной. Подстановка позволяет свести решение неравенства или уравнения к двум или нескольким более простым неравенствам или уравнениям. Решая неравенство
f(x) ,,), можно сделать подстановку либо в самим неравенстве, либо при решении уравнения f(x) = 0 (третий шаг метода интервалов). Поясним это на примере. Достаточно часто, используя метод постановки, удается понизить степень уравнения или неравенства.

Пример 1. Решить неравенство х 4 — х 2 — 20.

Пусть t = х 2 . После такой подстановки получится неравенство t 2 — t — 20, которое мы решим методом интервалов.

ОДЗ: tR.

f(t) = t 2 — t — 2; эта функция непрерывна на всей области определения.

f(3) = 3 2 — 3 — 2 = 4 > 0;

Таким образом, функция f(t) = t 2 — t — 2 — t — 2 — t — 2 принимает значения небольшие 0, если -1t2. Осуществим обратный переход к переменной x, тогда -1x 2 2. Это двойное неравенство равносильно системе неравенстви, следовательно, x[-;].

Решение 2. Решим неравенство x 4 — x — 20 методом интервалов.

ОДЗ: xR.

Решим биквадратное уравнение х 4 — x 2 — 2 = 0.

Пусть t = x 2 , t 2 — t — 2 = 0, отсюда t₁ = — 1, t₂ = 2.

Производим обратный переход к переменной x.

x 2 = -1 (нет корней); x 2 = 2, x₁ = —, x₂ =.

Вычисляем значения функции f(x) = x 4 — x 2 — 2,

f(2) = 2 4 — 2 2 -2 >0;

f(0) = 04 — 02 — 2 4 — (-2) 2 — 2 >0.

Таким образом функция f(x) принимает неположительные значения на промежутке [-;].

Ответ: x[-;].

Решение 1 дает возможность свести биквадратное неравенство к квадратному
t 2 — t — 20. Далее решение этого неравенства нужно «перевести с языка t на язык х». В этом и преимущество, и недостаток решения 1. Неравенство сводится к относительно простому, но переход от х к t может вызвать затруднения. Например, если бы t = х +, то пришлось бы решать систему

Решение 2 хорошо тем, что оно дает окончательный ответ. Недостаток этого способа: при решении более сложных примеров есть опасность ошибиться в вычислениях знака функции на интервалах знакопостоянства.

Пример 2. Решить неравенство7 — x.

При решении неравенств, содержащих квадратные корни, необходимо помнить, что возведение в квадрат обеих частей неравенства, сохраняя знак неравенства, можно лишь тогда, когда обе части неравенства принимают неотрицательные значения. Если же обе части неравенства принимают неположительные значения при возведении в квадрат необходимо изменить знак неравенства на противоположный. В перечисленных случаях возможны появления посторонних решений. Возведение неравенства в квадрат в тех случаях, кода части неравенства имеют противоположные знаки, т. е. одна часть принимает неотрицательные значения, а другая неположительные значения может привести к потере решений.

Введем вспогательную переменную. Пусть t =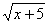, где t0, (из определения квадратного корня)
тогда t 2 = x + 5; откуда x = t 2 — 5 и имеем неравенство t7 — t 2 + 5;

t 2 + t — 120;

ОДЗ: tR.

f(t) = t 2 + t — 12; эта функция непрерывна на всей области определения. Формулу, задающую функцию, удобнее записать так f(x) = (x — 3)(x + 4).

f(4) =4 2 + 4 — 12 = 8 >0;

Таким образом, функция f(t) = t 2 + t — 12 принимает значения небольшие 0, если -4t3. Так как t0, то 0t4. Осуществим обратный переход к переменной x, тогда

03. Так как все части неравенства неотрицательны, то возведем их в квадрат 0x + 59, откуда -5x4 и, следовательно,

x[-5; 3].

Ответ: x[-5; 3].

Пример 3. Решить неравенство 2x 2 — 8x + 6 > .

В левой части неравества вынесем 2 за скобки 2 (x 2 — 4x + 3) >и введем вспомогательную переменную.

Пусть t =, тогда t > 0 и 2t 2 > t; 2t 2 — t > 0; t(2t -1) > 0.

В левой части неравенства задана квадратная функция, в которой старший коэффициент равен 1, а нули 0 и 0,5. Из свойств этой функции следует:

Таким образом неравенство 2t 2 > t равносильно неравенству t > 0,5.

Выполняем обратную замену переменных.

> 0,5, где x 3.

x 2 — 4x + 3 > 0,25;

4x 2 — 16x + 11 > 0;

D/4 = 64 — 44 = 20, D > 0.

x₁ =, x₂ =

Нетрудно установить, что 0,5 2 x — 3sinx — 2 2 — 3t — 2 2 — 42(-2) = 9 + 16 = 25, следовательно, D > 0.

3) t₁ = -0,5; t₂ = 2, поэтому решением неравенства является множество чисел
t(-; — 0,5)(2; +) (2).

Пересечение множеств (1) и (2) есть множество [-1; -0,5).

Произведем обратный переход к переменной х, получим неравенство.

-1sinx lg() + 2.

Так как -х > 0 при x lg(-x) + 2. Пусть t =, получим квадратное неравенство t 2 — 3t + 4

Источник