Как решать разными способами отрезки

Как узнать на сколько сантиметров один отрезок длиннее другого, разными способами

Ответ или решение 2

Рассмотрим варианты определения разности длины отрезков.

Первый способ

Предположим, что у нас имеют два отрезка, каждый из которых имеет свою длину. Наша задача определить определить на сколько сантиметров один из отрезков больше другого.

определяемся с отрезками и первым способом решения:

• первый отрезок имеет длину X см и он больше второго отрезка;
• второй отрезок имеет длину Y cм и он меньше первого отрезка;
• нужно определить на сколько см первый отрезок больше второго.

В результате решением будет: X-Y= Z, где Z это величина в сантиметрах на которую первый отрезок больше другого. И характерность этого способа в том, что мы узнавали насколько именно сантиметров первый отрезок длиннее второго.

Второй способ

Второй способ также подразумевает наличие двух отрезков разной длинны. Но во втором способе нашей задачей будет определение длины отрезка, который нужно добавить до величины второго отрезка, чтобы достичь длины первого отрезка

В этом способе решение будет выглядеть как: Y+Z=X

Разница способов заключается в подходе, который зависит от условия задачи. Если нужно определить, на сколько один отрезок больше другого, мы пользуемся первым способом. Если нужно определить, какой длинны отрезок нужно добавить до второго отрезка, чтобы получить первым, тогда мы используем второй способ.

Оба способа одинаково хороши и отличаются лишь акцентом в задаче, который изначально ставиться для задания пути желаемого решения. В обеих случаях используется одинаковый логический подход, одна общая формула.

Способ 1. Необходимо измерить длину каждого отрезка, а затем вычислить их разность математическим способом.

Способ 2. Нужно совместить начала отрезков (при этом они должны располагаться на одной прямой) и измерить расстояние от конца одного отрезка до другого.

Источник

Отрезок. Ломаная линия

Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.

Рис. 1 Отрезок на прямой

Чтобы понять, о каком именно отрезке идет речь, называют концы этого отрезка , то есть две точки, ограничивающие его. Так, на рисунке 1 обозначен отрезок AB , лежащий на прямой a .

На одной прямой можно отметить бесконечное число отрезков . Например, на рисунке 2 изображена прямая c и точки M , O , N и P принадлежащие этой прямой. Они делят участок прямой на следующие отрезки:

Рис. 2 Несколько отрезков на прямой

Называть отрезок (то есть точки, которые являются его концами) можно как слева направо, так и справа налево. Так, в последнем примере «отрезок MN » и «отрезок NM » являются названиями одного и того же отрезка. Но принято, что при обозначении отрезка мы называем его конечные точки слева направо .

Отрезок делит прямую линию на три объекта (смотри рисунок 3):

• отрезок DE
• луч a с началом в точке D
• луч b с началом в точке E

То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.

Рис. 3 Отрезок и лучи прямой

В большинстве случаев в школьном курсе математики отрезки рассматриваются без привязки к прямой , которой они принадлежат. То есть, рисуют сам отрезок, а остальную часть прямой (образовавшиеся лучи) просто «отбрасывают».

Рис. 4 Отрезок без прямой

И наоборот, если продлить отрезок , нарисованный как на рисунке 4, в обе стороны за концы этого отрезка, то мы получим прямую , на которой лежит данный отрезок.

Если точки лежат на одной прямой с отрезком и находятся между концами этого отрезка, то говорят, что эти точки принадлежат отрезку .

Рис. 5 Отрезок и принадлежащие ему точки

Так, на рисунке 5 видно, что:

• (·) C ∈AB – точка C принадлежит отрезку AB;
• (·) D ∈AB – точка D принадлежит отрезку AB;
• (·) E ∉AB – точка E не принадлежит отрезку AB;
• (·) F ∉AB – точка F не принадлежит отрезку AB.

В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.

Точки, которые лежат на отрезке, делят его на более короткие отрезки . На рисунке 6 видно, что точка O поделила отрезок LM на меньшие отрезки LO и OM . Каждый из этих двух меньших отрезков называются частью отрезка .

Рис. 6 Отрезок и части отрезка

Построение и измерение отрезка

Произвольный отрезок можно построить двумя способами:

1. Отметить часть прямой линии, обозначив края этой части точками (рисунок 7-а).
2. Обозначить на листе бумаги (на плоскости) две произвольные точки и соединить их между собой прямой линией (рисунок 7-б).

Рис. 7 Построение произвольного отрезка

В отличие от прямой линии и луча, которые длятся бесконечно, отрезок имеет длину , поэтому его можно измерить .

Измерить отрезок можно:

• относительным способом (сравнить отрезки между собой);
• абсолютным способом (определить его длину измерительным инструментом).

Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).

После этого нужно перенести циркуль на второй отрезок и поставить одну иглу на любой его конец. Если вторая игла циркуля совпадает со вторым концом отрезка, тогда эти отрезки равны .

Рис. 8 Сравнение отрезков

На рисунке 8 видно, что:

• отрезок AB равен отрезку DE (записывают просто AB=DE);
• FG
• HK>AB

Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.

Длина отрезка – это расстояние между концами этого отрезка.

Равные отрезки — это такие отрезки, которые имеют одинаковую длину.

На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?

Рис. 9 Измерение длины отрезка

Кроме произвольного, также требуется построить отрезок определенной длины .

Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.

Рис. 10 Построение отрезка заданной длины

Отрезок — это самое короткое расстояние между двумя точками.

В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.

Рис. 11 Кривая, ломаная, отрезок

Ломаная линия

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

Вершинами ломаной линии называются концы отрезков , из которых она состоит.
Звеньями ломаной линии называются составляющие ее отрезки .
Смежные звенья – это звенья, которые имеют общие вершины .
Смежные звенья не могут принадлежать одной прямой.
Длина ломаной линии – это сумма длин всех входящих в ее состав звеньев.

На рисунке 12 видно, что:

• KLMN – ломаная линия;
• K, L, M, N – вершины ломаной KLMN;
• KL, LM, MN – звенья ломаной KLMN;
• KL и LM – смежные звенья;
• LM и MN – смежные звенья;
• KL и MN – не являются смежными звеньями.

Называют ломаную линию по названию ее вершин, соблюдая их последовательность. Так, называть ломаную на рисунке 11 как KLMN или NMLK – правильно , а MLKN или MNLK – не правильно .

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Название разомкнутой ломаной начинается с названия вершины, с которой она начинается. Замкнутую ломаную можно называть , начиная с любой ее вершины.

• ABCDE — замкнутая ломаная;
• FGHKLM — разомкнутая ломаная

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

На рисунке 13 у замкнутой ломаной ABCD два пересекающихся звена: BC ∩ DA , а у разомкнутой ломаной EFGHI – три: EF ∩ HI и FG ∩ HI .

Источник

Узнай длину каждого отрезка. Какой из них длиннее и на сколько сантиметров? Решить задачу разными способами.

Ответ или решение 1

Нам дан рисунок на котором изображены два отрезка http://bit.ly/2BiFMZ3 красный и зеленый. Нужно найти длины отрезков и на сколько один отрезок длиннее второго разными способами.

Чтобы решить задачу будем действовать по следующему алгоритму действий

• на рисунке помимо отрезков изображена еще и линейка, с помощью нее мы можем ответить на вопрос какая длина красного отрезка;
• вторым шагом мы можем с помощью линейка найти на сколько длина красного отрезка больше длинны зеленого;
• третьим шагом зная длину красного отрезка и на сколько зеленый отрезок меньше красного мы можем найти длину зеленого отрезка;
• второй способ решения задачи измерить длину двух отрезков, а затем найти на сколько один отрезок длиннее второго.

Узнаем длины отрезков и на сколько один отрезок длиннее второго

Первый способ решения задачи.

Смотрим на рисунок и определяем длину красного отрезка. Она равна 10 см.

Длину зеленого отрезка вычислить сложнее, так как его начало не совпадает с началом числового луча.

Зато мы можем сна рисунке увидеть на сколько красный отрезок длиннее зеленого.

Смотрим на рисунок и видим, что эта разница в длинах равна 3 см.

Теперь мы можем легко найти длину зеленого отрезка. Для этого из длины красного отрезка вычтем разницу в длинах красного и зеленого отрезков и получим длину зеленого отрезка.

10 см — 3 см = 7 см длина зеленого отрезка.

Второй способ решения задачи.

Длинна красного отрезка видна с рисунка и равна 10 см, берем линейку и меряем длину зеленого отрезка — он равен 7 см.

Разница в длине: 10 см — 7 см = 3 см.

Ответ: красный отрезок 10 см, зеленый отрезок 7 см, разница в длине 3 см.

Источник

Сравнение отрезков. Действия над отрезками.

Равные и неравные отрезки

Пусть нам даны два отрезка АВ и СD (рис.). Наложим отрезок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и отрезок АВ направим по отрезку CD. Если точка В совпадаете точкой D, то отрезки АВ и CD равны; АВ = CD.

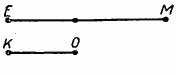
Сравним два отрезка КО и ЕМ (рис.).

Наложим отрезок КО на отрезок ЕМ так, чтобы точки К и Е совпали. Отрезок КО направим по отрезку ЕМ. Если точка О окажется где-нибудь между точками Е и М, то говорят, что отрезок ЕМ больше отрезка КО; отрезок КО меньше отрезка ЕМ.

Записывается это тaк: ЕМ > КО, КО 1 /₅ часть отрезка МN.

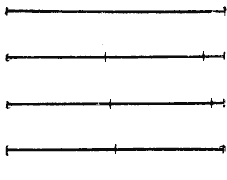
в) Чтобы разделить отрезок на равные части с помощью циркуля, поступают таким образом. Например, если нужно разделить отрезок на две равные части, то циркуль раздвигают на глаз так, чтобы раствор циркуля составлял примерно половину отрезка. Затем на данном отрезке от его конца последовательно один за другим откладывают этим раствором циркуля два отрезка. Если полученная сумма отрезков будет меньше данного отрезка, тo раствор циркуля увеличивают; если сумма окажется больше данного отрезка, то раствор циркуля уменьшают. Так, постепенно исправляя ошибку, можно отыскать довольно точнo половину отрезка (рис.).

Таким же образом выполняется приближённое деление отрезка на 3, 4, 5 и т. д. равных частей. Только в этом случае надо брать на глаз 1 /₃; 1 /₄; 1 /₅ . отрезка и откладывать взятый отрезок 3, 4, 5. раз, смотря по тому, на сколько равных частей надо разделить данный отрезок.

Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла

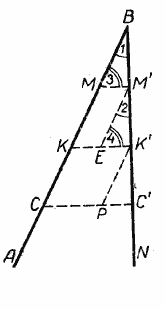
Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (рис.) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.

На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что ВМ’ = М’К’ = К’С’.

Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.

Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:

∠1 = ∠2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;

∠3 = ∠4, как острые углы 1 с соответственно параллельными сторонами (АВ || М’Е и ММ’ || КК’).

ВМ = МК по построению;

МК = М’Е, как противоположные стороны параллелограмма.

Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится.

Следовательно, ВМ = М’Е. Таким образом, ΔВММ’ = ΔМ’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’.

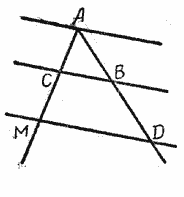
Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны.

В этом случае вершину угла на чертеже можно не отмечать (рис.).

Теорема справедлива и для случая, когда прямые КО и МР параллельны.

Пропорциональные отрезки

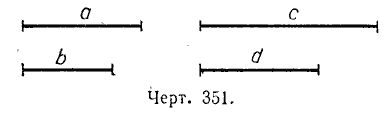
Из арифметики известно, что равенство двух отношений называется пропорцией. Например: 16 /₄ = 20 /₅; 2 /₃ = 4 /₆ To же самое имеем и в геометрии: если даны две пары отрезков, отношения которых равны, то можно составить пропорцию.

отрезки а, b, c, d называются пропорциональными.

Отношение a /_b называется, как и в арифметике, первым отношением, c /_d — вторым отношением; а и d называются крайними членами пропорции, b и с — средними членами.

В пропорции можно поменять местами отношения; можно переставить крайние члены, средние члены; можно переставить те и другие одновременно.

Поскольку в пропорции a /_b = c /_d под буквами подразумевают числа, выражающие длины отрезков, то произведение крайних членов её равно произведению средних членов. Отсюда, зная три члена пропорции, можно найти неизвестный четвёртый её член. Так, в пропорции a /_x = c /_d x = a • d /_c

Отметим ещё некоторые свойства пропорций, которыми придётся в дальнейшем пользоваться при доказательстве некоторых теорем и при решении задач.

а) Если три члена одной пропорции соответственно равны трём членам другой пропорции, то равны и четвёртые члены этих пропорций.

б) Если в пропорции равны предыдущие члены, то равны и последующие, т. е. если a /_x = a /_y , то х = у.

Чтобы убедиться в этом, переставим средние члены в этой пропорции.

А это возможно лишь в том случае, когда числитель и знаменатель дроби равны, т. е.

в) Если в пропорции равны последующие члены, то равны и предыдущие, т. е. если x /_a = y /_a , то х = у.

В справедливости этого свойства предлагается вам убедиться самостоятельно. Для этого проведите рассуждение, аналогичное предыдущему.

Построение пропорциональных отрезков

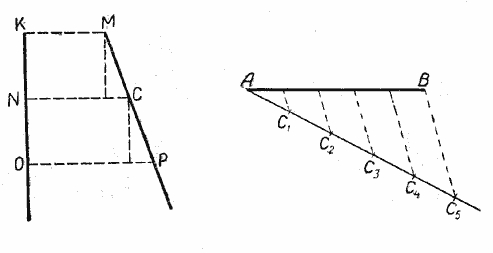
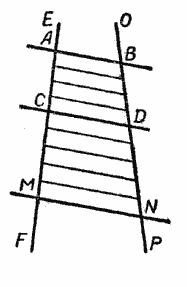
Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (рис.).

Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.

Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.

Например, р = 4 см. и q = 5 см.

Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на рисунке.

Тогда на прямой ОР отложатся равные между собой отрезки, при этом на отрезке BD их будет 4, а на отрезке DN — 5.

Отношение АС к СМ равно 4 /₅ , точно так же и отношение ВD к DN равно 4 /₅.

Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. AC /_AM = BD /_BN,

Теорема будет справедлива и при любых других целых значениях р и q.

Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.

Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых. Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток.

Источник