Решение нелинейных уравнений
Уравнения, в которых содержатся неизвестные функции, произведенные в степень больше единицы, называются нелинейными.
Например, y=ax+b – линейное уравнение, х^3 – 0,2x^2 + 0,5x + 1,5 = 0 – нелинейное (в общем виде записывается как F(x)=0).
Системой нелинейных уравнений считается одновременное решение нескольких нелинейных уравнений с одной или несколькими переменными.
Существует множество методов решения нелинейных уравнений и систем нелинейных уравнений, которые принято относить в 3 группы: численные, графические и аналитические. Аналитические методы позволяют определить точные значения решения уравнений. Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений. Численное решение нелинейных уравнений предполагает прохождения двух этапов: отделение корня и его уточнение до определенно заданной точности.
Отделение корней осуществляется различными способами: графически, при помощи различных специализированных компьютерных программ и др.
Рассмотрим несколько методов уточнения корней с определенно заданной точностью.
Методы численного решения нелинейных уравнений
Метод половинного деления.
Суть метода половинного деления заключается в делении интервала [a,b] пополам (с=(a+b)/2) и отбрасывании той части интервала, в которой отсутствует корень, т.е. условие F(a)xF(b)
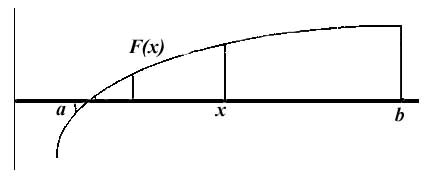
Рис.1. Использование метода половинного деления при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0, то начала отрезка a переносится в x (a=x), иначе, конец отрезка b переносится в точку x (b=x). Полученный отрезок делим опять пополам и т.д. Весь произведенный расчет отражен ниже в таблице.
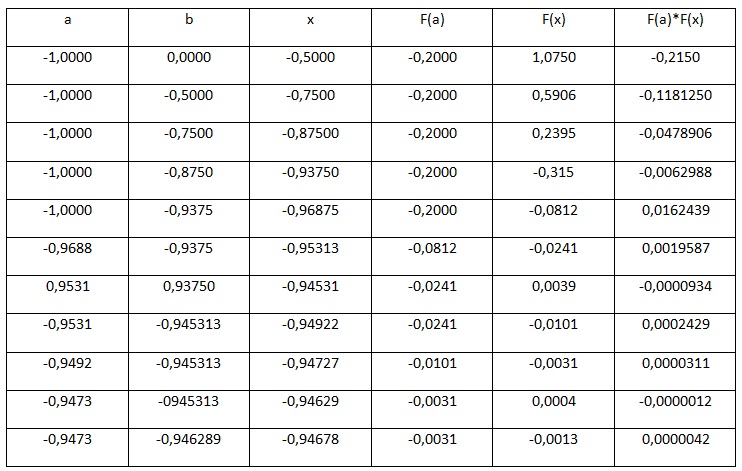
Рис.2. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
При использовании метода хорд, задается отрезок [a,b], в котором есть только один корень с установленной точностью e. Через точки в отрезке a и b, которые имеют координаты (x(F(a);y(F(b)), проводится линия (хорда). Далее определяются точки пересечения этой линии с осью абсцисс (точка z).
Если F(a)xF(z)
Рис.3. Использование метода хорд при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0;
Определим вторую производную F’’(x) = 6x-0,4.
F’’(-1)=-6,4 0 соблюдается, поэтому для определения корня уравнения воспользуемся формулой:
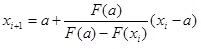
, где x0=b, F(a)=F(-1)=-0,2
Весь произведенный расчет отражен ниже в таблице.
Рис.4. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
Метод касательных (Ньютона)
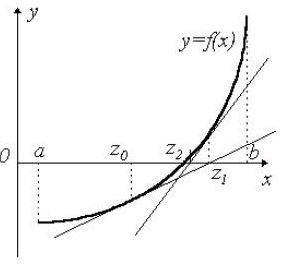
Данный метод основывается на построении касательных к графику, которые проводятся на одном из концов интервала [a,b]. В точке пересечения с осью X (z1) строится новая касательная. Данная процедура продолжается до тех пор, пока полученное значение не будет сравним с нужным параметром точности e (F(zi)
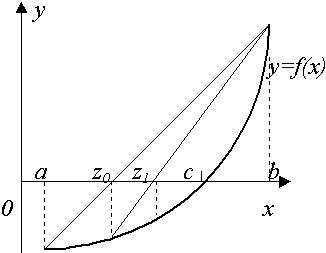
Рис.5. Использование метода касательных (Ньютона) при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0 выполняется, поэтому расчеты производим по формуле:
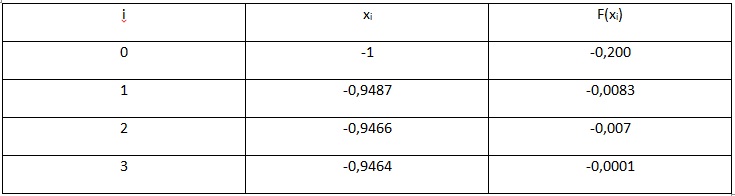
Весь произведенный расчет отражен ниже в таблице.
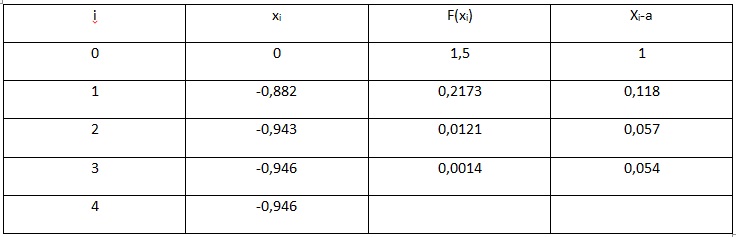
Рис.6. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Источник
Вопрос 3.Решение нелинейных уравнений. Графический метод



При решении уравнения F(x) = 0прежде всего важно предварительно изучить расположение корней и заключить каждый корень в малую область, содержащую только один корень. Эту операцию удобно выполнять с использованием пакета MathCAD
(Лабораторная работа №2).
Для этой цели часто применяют графические методы. Если требуется найти только действительные корни уравнения, то для отыскания грубых значений корней можно построить график функции F(x) = 0и найти абсциссы точек пересечения графика с осью X. Эти приближенные значения точек пересечения графика функции с осью X и принимают за начальные приближения к корням уравнения.
Если уравнение не имеет близких между собой корней, то этим способом они легко отделяются.
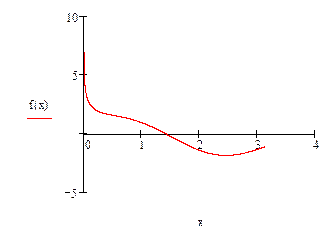
Иногда удобно представить уравнение F(x) = 0в виде F1(x) = F2(x)и затем, построив графики функций y1 = F1(x)и y2 = F2(x),найти абсциссы точек пересечения, которые и будут приближенными значениями корней.
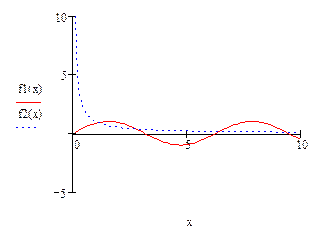
Корни уравнения симметричны относительно X=0. Поэтому мы можем рассматривать только положительные корни.
Значения x1, x2, x3 и еще нескольких корней можно довольно точно определить графически. Но на графике не будет xn для больших значений n. Значения xn при больших n будут близки к πn.
Эти значения можно уточнить.
Пусть 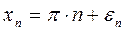
где εn – некоторые небольшие добавки.
Т.к. 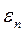
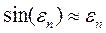
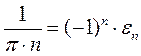

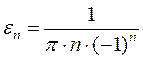
В результате получим улучшенное значение корня
Преимущества графического метода решения – удобство и простота. Недостаток – данный метод применим только для грубого отделения корня.
Источник
Графический метод решения задач нелинейного программирования
Чтобы найти ее оптимальное решение, нужно выполнить следующие действия:
- Найти ОДР, определяемую ограничениями задачи. Если окажется, что эта область пуста, то это означает, что задача не имеет решения.
- Построить семейство линий уровня целевой функции f(х1, х2) = C при различных значениях числового параметра С.
- При решении задачи на минимум определить направление убывания, а для задачи на максимум — направление возрастания линий уровня ЦФ.
- Найти точку ОДР, через которую проходит линия уровня с наименьшим в задаче на минимум (соответственно, наибольшим в задачи на максимум) значением параметра С. Эта точка будет оптимальным решением. Если ЦФ не ограничена снизу в задаче на минимум (сверху — в задаче на максимум), то это означает, что задача не имеет оптимального решения.
- Найти координаты точки оптимума и определить в ней значение ЦФ.
Отметим, что в отличие от задачи ЛП точка оптимума в задаче НП не обязательно находится на границе ОДР. Ею также может быть внутренняя точка этого множества.
Пример . В задаче выпуклого программирования требуется:
- найти решение графическим методом;
- написать функцию Лагранжа и найти ее седловую точку, используя решение, полученное графически.
F(X) = x1 2 +(x2-2) 2
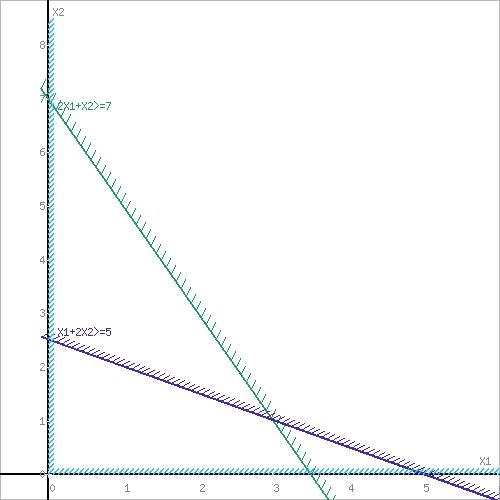
2x1+x2 ≥ 7
x1+2x2 ≥ 5
Решение. 1) Строим два ограничения, тем самым определяя ОДР. Можно использовать этот калькулятор. Также удобно строить ограничения через этот сервис.
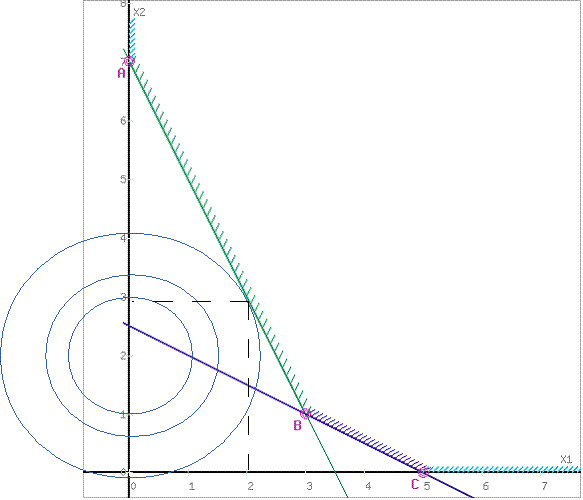
Затем строим функцию цели. В данном случае это окружность.
Поскольку задача минимума, то ищем первое касание линии уровня области ОДР. В данном случае это точка пересечения с прямой 2x1+x2-7=0.
Найдем точку пересечения. Для этого построим уравнение касательной, проходящей через центр окружности O(0;2) и перпендикулярно прямой 2x1+x2-7=0 (можно использовать этот калькулятор). Получаем: 2x2-x1-4=0. Решая систему уравнений:
2x1+x2-7=0
2x2-x1-4=0,
получаем: x1=2, x2=3.
2) Найдем экстремум функции F(X) = x1 2 +(x2-2) 2 , используя калькулятор Функция Лагранжа :
L( X , λ )=F( X )+∑(λi·φi)
где F( X ) — целевая функция вектора X; φi(X) — ограничения в неявном виде (i=1..n)
В качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция: F(X) = x1 2 +(x2-2) 2
Перепишем ограничение задачи в неявном виде:
φ1(X) = 7 — (2*x1+x2) = 0 (X1)
φ2(X) = 5 — (x1+2*x2) = 0 (X2)
Составим вспомогательную функцию Лагранжа: L(X, λ) = x1 2 +(x2-2) 2 — λ1*(7 — (2*x1+x2)) — λ2*(5 — (x1+2*x2))
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенным множителям λ.
Составим систему:
∂L/∂x1 = 2*λ1+λ2+2*x1 = 0
∂L/∂x2 = λ1+2*λ2+2*x2-4 = 0
∂L/∂λ1 = 2*x1+x2-7 = 0
∂L/∂λ2 = x1+2*x2-5 = 0
Решив данную систему, получаем:
а) для случая X1: x1 = λ1/2 + λ2 + 2; x2 = 7 — 2x1
Откуда можно найти такие λ1 ≥ 0, λ2 ≥ 0. Пусть λ2 = 0. Тогда λ1 = 2; x1 = 2; x2 = 3.
Поскольку λ2 ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Zmin(2;3)=5
б) для случая X2: x2 = λ1/2 + λ2 + 2; x1 = 5 — 2x2
Откуда можно найти такие λ1 ≥ 0, λ2 ≥ 0. Пусть λ2 = 0. Тогда λ1 = 2/5; x1 = 11/5; x2 = 3/5.
Поскольку λ1 ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Zmin(11/5;3/5)=6.8
Минимальное значение составит Zmin(2;3)=5.
Источник
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; \найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Источник

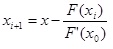



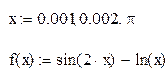
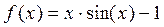
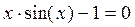
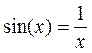
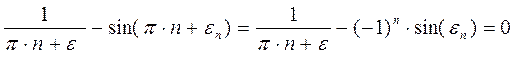
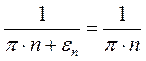

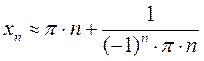















 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):



