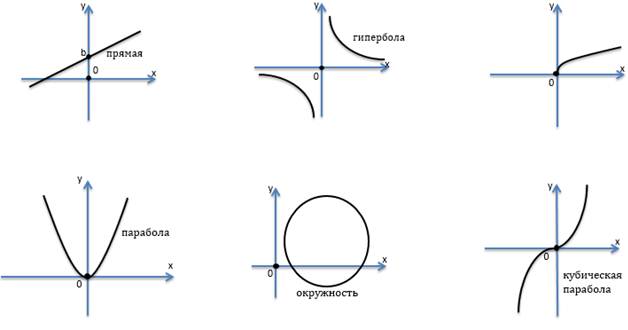
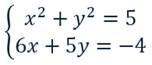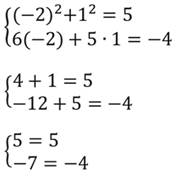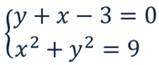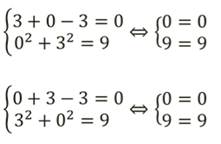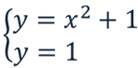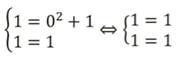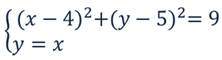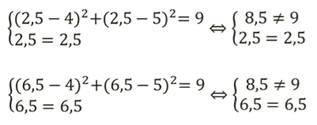- Системы уравнений с двумя переменными
- п.1. Понятие системы уравнений с двумя переменными и её решения
- п.2. Графический метод решения системы уравнений с двумя переменными
- п.3. Примеры
- Графический способ решения систем уравнений
- Урок 16. Алгебра 9 класс ФГОС
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Графический способ решения систем уравнений»
- Графический способ решения систем уравнений (9 класс)
- Как решать графический способ решения систем уравнений 9 класс
- Графический метод
- Пример 1
- Пример 2
- Пример 3
- Пример 4
- Пример 5
- Видео YouTube
Системы уравнений с двумя переменными
п.1. Понятие системы уравнений с двумя переменными и её решения
п.2. Графический метод решения системы уравнений с двумя переменными
Поскольку каждое из уравнений с двумя переменными можно изобразить в виде графика на плоскости, графический метод решения систем таких уравнений достаточно удобен.
п.3. Примеры
Пример 1. Решите графическим способом систему уравнений:
а) \( \left\< \begin
\( \mathrm
\( \mathrm <4x+3y=0>\) – прямая \( \mathrm
Система имеет два решения (–3; 4) и (3; –4)
Ответ: <(–3; 4) ; (3; –4)>.
б) \( \left\< \begin
\( \mathrm
y – x = 4 – прямая y = x + 4
Система имеет два решения (–5; –1) и (1; 5)
Ответ: <(–5; –1) ; (1; 5)>.
в) \( \left\< \begin
x 2 + y = 1 – парабола y = –x 2 + 1
x 2 – y = 7 – парабола y = x 2 – 7
Система имеет два решения (–2; –3) и (2; –3)
Ответ: <(–2; –3) ; (2; –3)>.
г) \( \left\< \begin
xy = 1 – гипербола \( \mathrm
x 2 + y 2 = 2 – окружность с центром в начале координат, радиусом \( \mathrm<\sqrt<2>> \)
Система имеет два решения (–1; –1) и (1; 1)
Ответ: <(–1; –1) ; (1; 1)>.
Пример 2*. Решите графическим способом систему уравнений
a) \( \left\< \begin
x 3 – y = 1 – кубическая парабола y = x 3 – 1, смещённая на 1 вниз.
\( \mathrm <\frac1x-y=1>\) – гипербола \( \mathrm
Система имеет два решения (–1; –2) и (1; 0)
Ответ: <(–1; –2) ; (1; 0)>.
б) \( \left\< \begin
|x| + |y| = 2 – квадрат с диагоналями 4, лежащими на осях
x 2 + y 2 = 4 – окружность с центром в начале координат, радиусом 2
Система имеет четыре решения (2; 0), (0; 2) , (–2; 0) и (0; –2)
Ответ: <(2; 0) ; (0; 2) ; (–2; 0) ; (0; –2)>.
в) \( \left\< \begin
y – x 2 = 4x + 6 – парабола y = (x 2 + 4x + 4) + 2 = (x + 2) 2 + 2, ветками вверх, смещённая на 2 влево и на 2 вверх
y + |x| = 6 – ломаная, y = –|x| + 6. Для x > 0, y = –x + 6, для x 0, y = x, для x
Источник
Графический способ решения систем уравнений
Урок 16. Алгебра 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Графический способ решения систем уравнений»
Графиками таких уравнений могут являться различные линии.
Решить систему — значит найти все её решения или доказать, что их нет.
Решением системы называется пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство.
Нужно проверить, обращают ли пара значений уравнения системы в верные равенства.
1. Первая пара (-2, 1). Подставим их в систему:
Первое уравнение обратилось в верное равенство, а второе — нет. Значит, пара чисел (-2;1) не является решением данной системы.
2. Вторая пара (1;-2). Поставим эти значения в систему:
Получаем два верных равенства. Значит, пара чисел (1;-2) является решением данной системы.
Решить систему двух уравнений:
Изобразим график системы:
Видим, что графики пересеклись в двух точках. Их координаты и являются решением системы. Данная система имеет два решения: (0;3) и (3;0).
Проверим, действительно ли они являются решениями. Подставим эти значения в систему:
Проверка необходима потому, что графический метод позволяет получить приближённые значения. Иногда их сложно указать точно.
Получили две пары значений: (0;3) и (3;0).
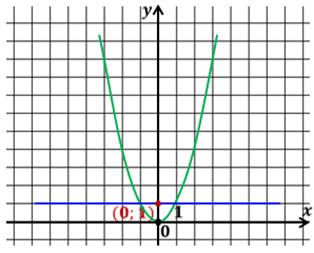
Решить систему уравнений:
Изобразим график системы:
Точку пересечения этих графиков имеет координаты (0;1). Подставим значения в систему:
Получили верные равенства. Значит, решением данной системы является пара чисел (0;1).
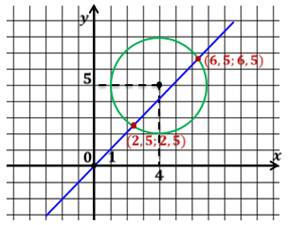
Решить систему двух уравнений:
Изобразим график системы:
Видим две точки пересечения. Их координаты трудно указать точно. Поэтому прежде чем записать ответ, полученные значения нужно подставить в систему:
Решением системы будут две пары чисел(2,5;2,5) и (6,5;6,5).
Источник
Графический способ решения систем уравнений (9 класс)
Выбранный для просмотра документ графический способ решения систем уравнений.ppt
Описание презентации по отдельным слайдам:
Французский писатель Анатоль Франс «Учиться можно только весело … Чтобы переваривать знания, надо поглощать их с аппетитом»
Тест Проанализируйте уравнения. Выберите, уравнение, соответствующее данному графику:
y=x+1 y+1=0 y=1 xy=1 2
xy=-1 x+y=2 х²+y²=25 xy=1 3
Проверь себя: y=-x²+1 у = — 1 xy=1 у=|х| х²+y²=1
Решить систему уравнений
Графический способ решения систем уравнений.
Задание 1. Решить графически систему уравнений. 1. 2. Построим графики функций в одной системе координат. 3. Составим таблицы значений функций. х -3 -2 -1 0 1 2 3 у 9 4 1 0 1 4 9 х 0 -3 у 3 -3
Задание 1. Ответ: ( -1; 1); (3; 9) А В х 0 -3 у 3 -3 х -3 -2 -1 0 1 2 3 у 9 4 1 0 1 4 9
Задание 2. Решить графически систему уравнений. 1. 2. Построим графики функций в одной системе координат. 3. Составим таблицы значений функций. х -8 -4 -2 -1 1 2 4 8 у -1 -2 -4 -8 8 4 2 1 х 0 -3 у -3 0
Задание 2. Ответ: решений нет х -8 -4 -2 -1 1 2 4 8 у -1 -2 -4 -8 8 4 2 1 х 0 -3 у -3 0
Задание 3. Решить графически систему уравнений. Подробно х 0 3 у 3 -3 х -4 -2 -1 1 2 4 у 0,5 1 2 -2 -1 -0,5
х – любое действительное число. 1. 2. Графиком функции является парабола, ветви которой направлены вверх. a > 0 3. Найдём координаты вершины параболы 4. Дополнительные точки: М ( 2; -1) х 0 1 2 3 4 5 у 3 0 -1 0 3 8
Решить графически системы уравнений 1 2 3
Самостоятельно. Решить графически систему уравнений. Проверка (2) Ответ: ( -3; 4); (3; 4); (-1; 4,9); (1; 4,9)
Самостоятельно. Решить графически систему уравнений. Проверка (2) Ответ: решений нет
Самостоятельно. Решить графически систему уравнений. Проверка (2) Ответ: (2; 4)
Рефлексия: Мизинец – Мне сейчас … Безымянный – Я хочу … Средний – Я буду… Указательный – Чего я жду от урока… Большой – Мне интересно …
Домашнее задание: Выполнить дома: №418, №421 (а,б)
Выбранный для просмотра документ урок в 9 а классе Графический способ решения систем уравнений.docx
Тип урока: урок нового знания
Тема урока: Графический способ решения систем уравнений
— дидактические: организация деятельности учащихся по восприятию, осмыслению, первичному запоминанию и закреплению знаний по теме « Графический способ решения систем уравнений »; обобщение и углубление знаний, умений учащихся применять графические способы решения уравнений и систем уравнений и их комбинаций;
— развивающие: развитие логического мышления, культуры графического построения, наблюдательности, памяти, умения анализировать, сравнивать и делать выводы;
— воспитательные: средствами учебного занятия создать условия, способствующие формированию умения искать пути выхода из затруднения.
— предметные: освоение учащимися новой темы « Графический способ решения систем уравнений » и применение её при решении задач;
— метапредметные (регулятивные – Р, коммуникативные – К, познавательные – П): умение определять понятия, создавать обобщения, устанавливать аналогии, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение и делать выводы;
— личностные (Л) – установление учащимися связи между целью учебной деятельности и ее мотивом.
Оборудование: м ультимедийный проектор, экран, компьютер, электронные презентации для устной работы и изучения новой темы, выполненная в Microsoft Power Point,
(указать цель на каждом этапе)
(с указанием форм деятельности)
Формируемые УУД (конкретные)
1. Мотивация к учебной деятельности
выработка на личностно значимом уровне положительного самоопределения ученика к деятельности на уроке
Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело … Чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием.
Перед вами лежит листок бумаги. Обведите на нём свою руку. Продолжите предложения, характеризующие ваше эмоциональное состояние в данный момент:
Мизинец – Мне сейчас …
Безымянный – Я хочу …
Средний – Я буду…
Указательный – Чего я жду от урока…
Большой – Мне интересно …
Организация рабочего места, постановка перед собой целей
-действовать, запоминать, усваивать
К: планирование учебного сотрудничества
2. Актуализация знаний (5-7 мин) Цель: формулирование цели и темы урока
Повторение: Что называется графиком уравнения с двумя переменными?
В тетрадях записать уравнение, которое соответствует данному графику.
Взаимопроверка: обменяться тетрадями и проверить. Слайд 8
Решить систему уравнений:
Уравнения какой степени входят в систему уравнений?
В 7 классе мы рассматривали системы уравнений первой степени с двумя переменными. Теперь займёмся решением систем, составленных из двух уравнений второй степени или из одного уравнения первой степени, а другого второй степени.
Вспомним, что решением системы двух уравнений с двумя переменными является пара чисел, обращающая каждое уравнение системы в верное равенство. Решить систему – значит найти все её решения или доказать, что решений нет.
Какие способы решения систем уравнений вы знаете?
Тема нашего урока «Графический способ решения систем уравнений»
Перед вами стоит задача – показать свои знания и умения по решению систем уравнений с помощью графиков.
Источник
Как решать графический способ решения систем уравнений 9 класс
Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться , такую группу уравнений мы называем системой.
Объединяем уравнения в систему с помощью фигурной скобки:
Графический метод
Недаром ответ записывается так же, как координаты какой-нибудь точки.
Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Например, построим графики уравнений из предыдущего примера.
Пример 1
Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):
Для того чтобы графически решить систему уравнений с двумя переменными нужно:
1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);
Разберем это задание на примере.
Решить графически систему линейных уравнений.
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Пример 2
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Пример 3
Графическое решение системы
Пример 4
Решить графическим способом систему уравнений.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Пример 5

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.
Видео YouTube
Источник