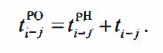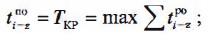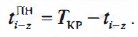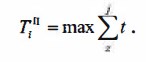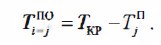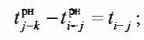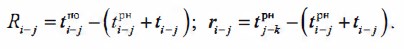Как рассчитать сетевой график табличным способом

Анализ сетевого графика

Выберите нужный тип вершины и нажмите левой кнопкой мыши на графическом полотне

Размеры графического полотна

Созданный сетевой график можно сохранить в форматах docx и png (меню Действия ). Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).

Инструкция к сервису

Основные определения

На сетевой модели событиям соответствуют вершины графа.

Правила построения сетевой модели

Правило 2 . Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.

Правило 3 . При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:
а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?
б) Какие операции должны непосредственно следовать после завершения данной операции?
в) Какие операции могут выполняться одновременно с рассматриваемой?

При построении сетевого графика следует соблюдать следующие правила:

• в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
• В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
• в сети не должно быть замкнутых контуров (рис.1);
• Любые два события должны быть непосредственно связаны не более чем одной работой.
• В сети рекомендуется иметь одно исходное и одно завершающее событие.
• Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелка
завершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.

Источник

Сетевое планирование и управление

2.2. Практическое занятие по структурному планированию

Целью занятия является получение навыков составления сетевых графиков, расчета раннего и позднего времени начала работ , нахождения критического пути.

Форма занятия – практическое занятие с использованием рабочей тетради.

Продолжительность – два академических часа.

2.2.1. Пример составления и расчета сетевого графика

Предположим, что мы составляем проект Внедрение бухгалтерской системы для небольшой бухгалтерии, содержащей порядка 10 рабочих мест.

Этап 1. Составление перечня работ

В результате анализа выделяем перечень работ по проекту и оцениваем их длительность в днях. Результаты заносим в табл.2.4.

Таблица 2.4.

№	Название работы	Длительность
1	Начало проекта	—
2	Выбор системы	15
3	Приобретение программного обеспечения	7
4	Составление проекта сети	7
5	Приобретение компьютеров и сетевого оборудования	15
6	Обучение администратора и программиста	30
7	Монтаж локальной сети	20
8	Установка ПО на компьютеры	5
9	Установка сетевого ПО, настройка сети	25
10	Ввод начальных данных в информационную базу	40
11	Обучение персонала	30
12	Передача в эксплуатацию	5
13	Конец проекта	—

Этап 2. Определение взаимосвязей между работами

Для каждой работы из табл.2.4 требуется установить номера тех работ, до окончания которых она не может быть начата. Результат заносится в табл.2.5.

Таблица 2.5.

№	Название работы	Предшественники
1	Начало проекта	—
2	Выбор системы	1
3	Приобретение программного обеспечения	2
4	Составление проекта сети	2
5	Приобретение компьютеров и сетевого оборудования	2
6	Обучение администратора и программиста	4
7	Монтаж локальной сети	4; 5
8	Установка ПО на компьютеры	3; 5
9	Установка сетевого ПО, настройка сети	6; 7; 8
10	Ввод начальных данных в информационную базу	9
11	Обучение персонала	9
12	Передача в эксплуатацию	10; 11
13	Конец проекта	—

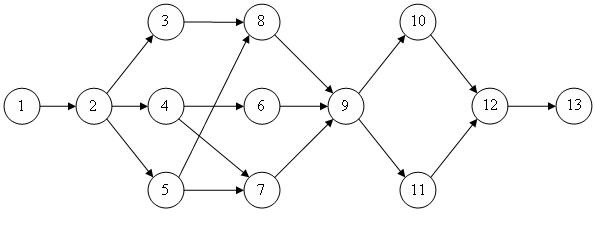
Этап 3. Составление сетевого графика работ

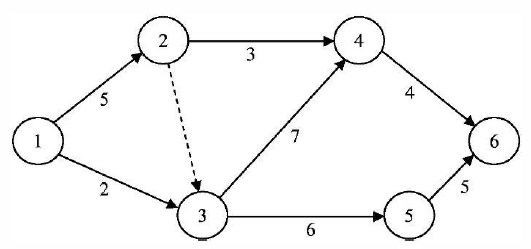
Каждая из работ табл.2.5 на сетевом графике обозначается кружком, в который заносится ее номер. Кружки соединяются стрелками. Стрелка соответствует одному из чисел столбца Предшественники и соединяет работу-предшественник с работой-последователем. Результат изображен на рис.2.9.

Этап 4. Вычисление раннего времени начала работ

В соответствии со схемой, приведенной на рис.2.2 вычисляем раннее время начала работ с учетом их длительностей из табл.2.4 и связей, задаваемых сетевым графиком на рис.2.9. Вычисления начинаются с первой и заканчиваются последней работой проекта. Последовательность вычислений приведена в табл.2.6. Результат показывает, что длительность проекта равна 122 дня.

Источник

18.3 Расчет сетевых графиков

Расчет сетевых графиков сводиться к численному определению его пара-метров. Поэтому сначала перечислим их.

При расчете сетевых графиков определяются следующие параметры:

— ранние начала и окончания работ;

— поздние начала и окончания работ;

— продолжительность критического пути;

— общие и частные резервы работ.

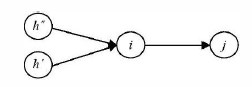
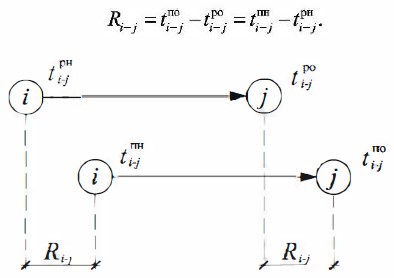
За расчетную схему (рис. 18.8) выберем расположение работ, закодирован­ных буквами: h — предшествующая работа, i — рассматриваемая работа,j — после­дующая работа.

​

Рис. 18.8 Расчетная модель

Раннее начало работы — самый ранний из возможных сроков начала рабо­ты, который обуславливается выполнением всех предшествующих работ.

Раннее начало работы (рис. 18.9) равно продолжительности максимально­го пути от исходного события графика до начального события данной работы:

​

Рис. 18.9 Модель расчета ранних начал

Раннее окончание работы — самый ранний из возможных сроков окончания работы. Оно равно сумме раннего начала работы и ее продолжительности:

​

Для начальных (исходных) работ:

— раннее начало принимается равным 0;

— раннее окончание численно равно продолжительности работы. Максимальное раннее окончание одной из завершающих работ определяет продолжительность критического пути.

Позднее начало работы — самый поздний допустимый срок начала работы, при котором планируемый срок достижения конечной цели не меняется.

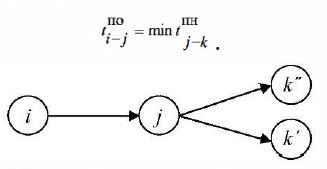
Позднее окончание работы определяется разностью между продолжитель­ностью критического пути и продолжительностью максимального пути от ко­нечного события данной работы до завершающего события графика.

Позднее окончание любой работы (рис. 18.1 О) равно наименьшему из поздних начал последующих работ:

​

Рис. 18.10 Модель расчета поздних окончаний

Позднее начало работы равно разности между величинами ее позднего окончания и продолжительности.

Для завершающих работ сетевого графика:

— позднее окончание равно величине продолжительности критического пути:

​

= позднее начало завершающей работы равно разности между продол­жительностью критического пути и продолжительностью данной работы:

​

Общий (или полный) резерв времени работы R;-1 (рис. 18.11) — это макси­мальное время, на которое можно увеличить продолжительность данной рабо­ты или перенести ее начало без увеличения продолжительности критического пути. Он равен разности между одноименными поздними и ранними парамет­рами этой работы:

​

Рис. 18.11 Модель расчета общих резервов

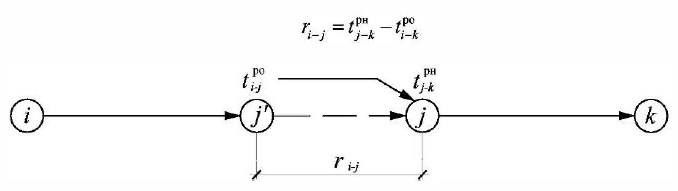
Частный резерв времени (рис. 18.12) — это максимальное время, на которое можно увеличить продолжительность данной работы или перенести ее начало без изменения ранних сроков начала последующих работ. Он равен разности между ранним началом последующей работы и ранним окончанием данной работы:

​

Рис. 18.12 Модель расчета частных резервов

Частный резерв времени отличается от нуля, если в конечное событие ра­боты входят две и более работы.

Методы расчета сетевых графиков

Сетевые графики можно рассчитывать с помощью компьютерной техники и вручную. В настоящее время известно несколько методов расчета сетевых графиков вручную: табличный метод; расчет на графике — четырехсекторный метод; метод дроби; метод потенциалов и др.

Классическим методом, положившим начало теории расчета сетевых гра­фиков, является табличный метод, или, как говорят, алгоритм расчета сетево­го графика по таблице.

Пример графика для расчета табличным методом приведен на рис. 18.13. В этом случае определение параметров сетевого графика выполняется в таблице.

​

Рис. 18.13 Пример графика для расчета табличным методом и методом потенциалов

Заполнение таблицы ведется в следующем порядке.

1) В первые три графы заносят исходные данные по каждой работе. Необходимо последовательно записывать все работы, выходящие из первого события ( по часовой стрелке), затем — все работы, выходящие из второго события:, и т.д.

2) Производят расчет ранних параметров работ построчно сверху вниз.

­3) Определяют продолжительность критического пути, равная максималь­ному из ранних окончаний завершающих работ.

4) Рассчитывают поздние параметры работ. Расчет ведется построчно сни­зу вверх, от завершающих работ до исходных.

5) Определяют общие и частные резервы времени (их можно определить по каждой работе вразбивку).

Определяют перечень работ, составляющих критический путь, т.е. работ, не имеющих резервов времени.

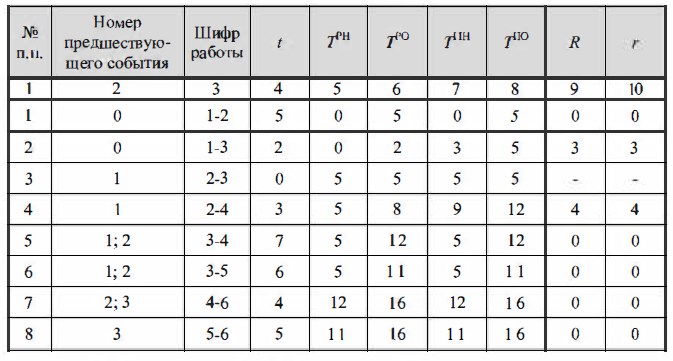
При расчете сетевых графиков табличным методом заполняют следующую таблицу (табл. 18.1).

Расчет сетевого графика

​

В графу 3 заносят шифр (код) каждой работы, запись ведут последова­тельно, начиная с первого события. Когда из события выходят несколько ра­бот, запись ведут в порядке возрастания номеров их конечных событий. После этой процедуры в графу 2 записывают номера событий, предшествующих каж­дой работе.

Следующей заполняют графу 4. Против каждой работы, записанной в гра­фе 3 из сетевого графика, проставляют её продолжительность t.

Графы 5 (раннее начало работы ТРН) и 6 (раннее окончание работы ТРН за­полняются одновременно. У работ 1-2 и 1-3 предшествующих событий нет; следовательно, их раннее начало равно нулю. Раннее окончание работы равно сумме его раннего начала и продолжительности . Таким образом, в графу 6 вно­сят сумму цифр граф 4 и 5. Для работы 2-4 раннее начало равно раннему окон­чанию предшествующей работы, т.е. работы 1-2 (в графе 2 записано предшест­вующее событие 1 ); следовательно, раннее начало работ, начинающихся с события 2 (2-3, 2-4), также равно 5 дням. Прибавляя к ранним началам работ их продолжительности, получим их раннее окончание. Если у работы есть два и более предшествующих события (например, работа 4-6), то в этом случае вы­бирают максимальное значение раннего окончания этих работ и заносят в гра­фу 5, и на ее основе определяют ранее окончание.

Максимальное раннее окончание последней работы равно величине кри­тического пути.

Дальше заполняют графы 7 и 8. Позднее начало ТПН и окончание ТПО запи­сываем в таблицу 18.1, начиная с конца графы.

Критический путь, а следовательно, и позднее окончание завершающей работы, равен 16 дням. Вносим эту цифру в строку 8 графы 8. Позднее начало работы равно разности его позднего окончания и продолжительности.

Общий резерв R (графа 9) определяют как разность между числами в гра­фах 8 и 6 или 7 и 5.

Частный резерв r (графа 10) подсчитывают как разность между ранним на­чалом последующей работы и ранним началом данной. При заполнении данной графы необходимо учитывать следующее, если в конечное событие данной ра­боты входит только одна стрелка, то частный резерв ее равен нулю. Для работ, не лежащих на критическом пути, но входящих в события, лежащие на нем, общие и частные резервы численно равны. Частные и общие резервы работ, лежащих на критическом пути, равны нулю.

Правильность расчета сетевого графика подтверждают проверкой:

— ранние параметры никогда не превосходят по численному значению поздние параметры;

— критический путь должен представлять собой непрерывную последова­тельность работ от исходного события до завершающего;

— величина частного резерва времени работы не должна превосходить ве­личину общего резерва времени;

— позднее начало одной из исходных работ обязательно должно быть ну­левым.

Расчет сетевых графиков методом потенциалов

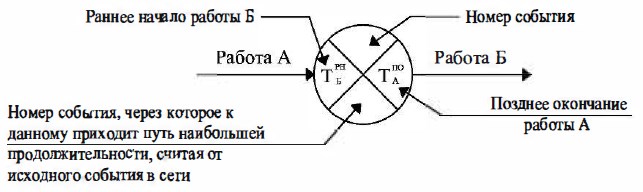
Потенциалом i-го события (ТjП ) называют величину наиболее продолжи­тельного пути от данного события до завершающего:

​

Потенциал события (рис. 18.14) показывает, сколько дней осталось от дан­ного события до завершения всех работ планируемой программы. Потенциал определяют последовательно, начиная от завершающего события сети.

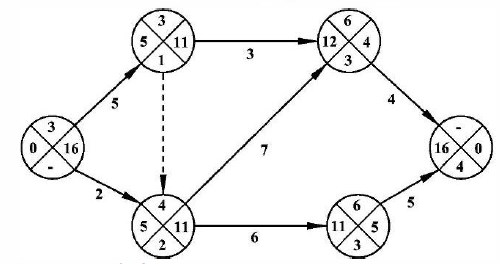
В качестве примера рассмотрим тот же график, размещенный на рис. 18.13. Расчет (рис. 18.15) начинают с завершающего события 6, потенциал ко­торого равен О. В верхний сектор ставим прочерк, в правый записываем О и пе­реходим к последующему событию.

​

Рис. 18.14 Запись в секторах при расчете методом потенциалов

​

Рис. 18.15. Пример расчета методом потенциалов

( номера событий соответствуют рис. 18.1 З)

Потенциал события 5 (продолжительность работы 5-6) равен 5 дням. Циф­ру 5 записываем в правый сектор события 5, цифру 6 — в его верхний сектор.

Потенциал события 4 Т4П = 0 + 4 = 4. Для события 2 потенциал определяют следующим образом: от события 3 — Т2П = 11 + О = 11 и от события 4 — Т2П = 4

+ 3 = 7; выбирают наибольшее значение 11. Аналогичным образом рассчиты­вают остальные события. Потенциал исходного события составляет 16 дней, т.е. равен величине критического пути.

Зная потенциал события, позднее окончание работ можно определить по формуле

​

Поскольку ранние начала работ записаны в левых секторах, а на графике показаны продолжительности работ, по уже приведенным формулам частного и общего резерва времени можно определить их значение.

Изменения, возникающие в ходе выполнения работ, не влияют на потен­циалы последующих событий; поэтому оперативный пересчет графика занимает мало времени. В этом заключается главное преимущество расчета методом потенциалов.

Четырехсекторпый ,метод расчета сетевых графиков

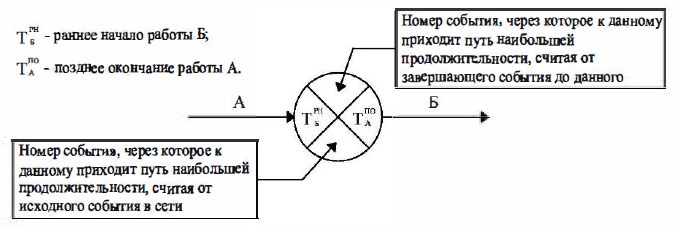
При этом методе каждое событие (рис. 18.16) графиком делится на 4 сек­тора, в которых указываются необходимые расчетные данные.

​

Рис. 18.16 Условные обозначения при четырехсекторном методе расчета

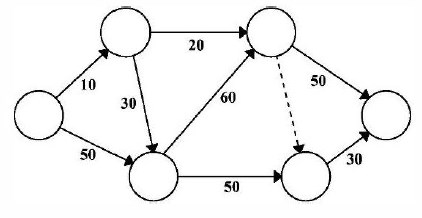
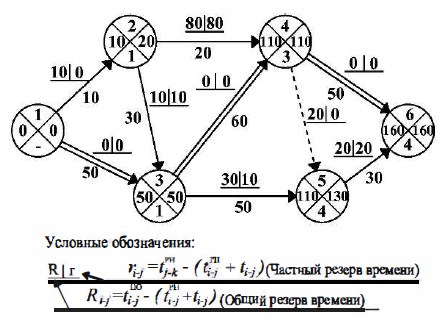
Исходным графиком для расчета четырехсекторным методом служит гра­фик, приведенный на рис. 18.17.

​

Рис. 18.17 Исходный график для расчета четырехсекторным методом

Вначале от исходного события до завершающего определяют все ранние начала работ.

Для завершающего события графика значения в левом и правом секторах равны, поскольку максимальное из ранних окончаний завершающей работы равно позднему окончанию этой работы.

Затем рассчитывают поздние окончания работ от завершающего к начально­му событию. Рассчитанный график будет иметь вид показанный на рис. 18.18.

Дополнительным требованием к критическим работам является требова­ние по соблюдению условия

​

20-12 = 8; 25-5 = 20; 25-11 = 12; следовательно, работы нижнего пути- не­критические.

​

Рис. 18.18 График, рассчитанный четырехсекторным методом

Резервы времени работ графика можно отметить на самом графике в виде Rr, а рассчитать их следует по формулам:

​

Четырехсекторный способ расчета сетевых графиков позволяет быстрее осуществить расчет и определить продолжительность критического пути (ино­гда требуется прикидочный расчет), но при повторном расчете требуется пере­бирать данные на графике. Этого не требуется при табличном способе, где пе­ресчитывается сама таблица. Кроме того, в таблице наглядно прослеживаются все без исключения параметры сетевого графика (включая резервы времени).

Построение сетевых графиков «вершины-работы»

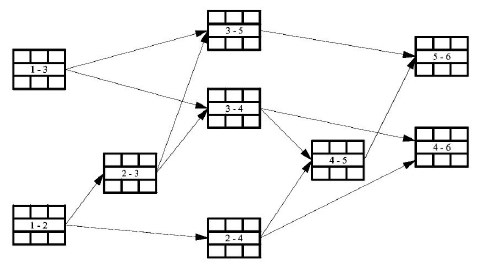
В последнее время построение сетевых графиков всё чаще выполняют по принципу «вершины-работы», а не по принципу «вершины-события», как это было в предыдущих примерах (рис.18.19).

Для расчета сетевого графика «вершины-работы>> прямоугольник, изобра­жающий работу, делят на 7 частей (рис. 18.20). В верхних трех частях прямо­угольника записывают раннее начало, продолжительность и раннее окончание работы, в трех нижних — позднее начало, резервы времени и позднее оконча­ние. Центральная часть содержит код (номер) и наименование работы.

Расчет сетевого графика начинают с определения ранних сроков. Раннее начало и окончание вычисляют последовательно от исходной до завершающей работы, раннее начало исходной работы равно О, раннее окончание — сумме раннего начала работы и ее продолжительности.

Раннее начало последующей работы равно раннему окончанию предыду­щей работы. Если работе непосредственно предшествует несколько работ, то ее раннее начало будет равно максимальному значению из ранних окончаний предшествующих работ.

​

Рис. 18.19 График типа «вершины-работы»

​

Рис. 18.20 Изображение работы в сетевом графике «вершины-работы»

Раннее окончание завершающей работы определяет продолжительность критического пути.

Расчет поздних сроков ведут в обратном порядке, от завершающей работы до исходной. Позднее окончание завершающей работы равно ее раннему окон­чанию, т.е. продолжительности критического пути.

Позднее начало определяют как разность позднего окончания и продолжи­тельности работы.

Полный ( общий) резерв времени, равный разности поздних и ранних сро­ков, заносят в числитель середины нижней части.

Частный резерв времени, равный разности между минимальным ранним началом последующих работ и ранним окончанием данной работы, записывают в знаменатель середины нижней части.

Частный резерв всегда меньше полного резерва работы или равен ему. По­следовательность работ с нулевыми резервами времени является критическим путем сетевого графика.

› Содержание › 18.3 Расчет сетевых графиков

Источник