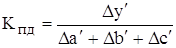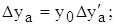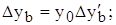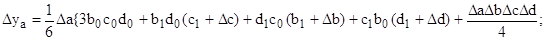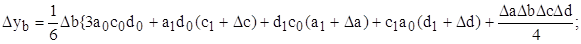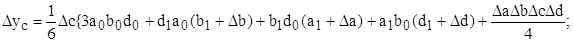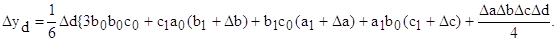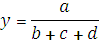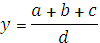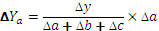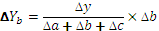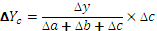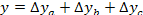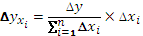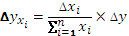Пропорциональное деление
Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.
Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.
Деление числа на пропорциональные части
Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.
Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:
Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:
Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.
90 : (1 + 2 + 3) = 90 : 6 = 15;
Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.
Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.
Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:
значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то
a = (66 : 33) · 15 = 30;
b = (66 : 33) · 10 = 20;
c = (66 : 33) · 8 = 16.
Второй способ: обозначим искомые части буквами a, b и c:
Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:
Следовательно, c равно:
| c = | 2 · 4 | = | 8 | , |
| 5 | 5 |
| a:b:c = 3:2: | 8 | . |
| 5 |
Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:
так как 15 + 10 + 8 = 33, то
a = (66 : 33) · 15 = 30;
b = (66 : 33) · 10 = 20;
c = (66 : 33) · 8 = 16.
Деление на части, обратно пропорциональные числам
Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как
| 1 | : | 1 | : | 1 | . |
| 2 | 3 | 5 |
Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:
Источник
Способ пропорционального деления или долевого участия
5. Способ пропорционального деления или долевого участия
Сущность способа пропорционального деления состоит в пропорциональном делении прироста результативного показателя по факторам его обусловившим, а долевого участия — в определении доли участия каждого фактора в общем приросте результативного показателя.
Эти способы применяются для аддитивных, мультипликативных, кратных и смешанных моделей типа 
.
Для определения влияния отдельных факторов на прирост результативного показателя рассчитывается один из следующих коэффициентов:
1) коэффициент пропорционального деления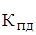 
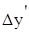
, как отношение общего относительного прироста результативного показателя 
к сумме относительных изменений факторных показателей.
При аддитивных типах моделей рассчитывается один коэффициент пропорциональности, а при других типах моделей — он определяется для каждого порядка факторов в отдельности.
При исходной модели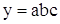 
, 
(изменения всех составляющих взяты в относительных единицах).
;
; 
;
.
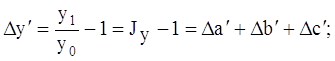
2) коэффициент долевого участия 
, который определяется как отношение относительного прироста i‑го факторного показателя к сумме относительных изменений факторных показателей.
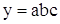
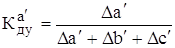
Например, для исходной факторной модели , коэффициент долевого участия для фактора «а»:
.
Тогда для приведенной исходной мультипликативной модели:
;
;
;
.
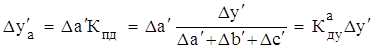
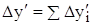
Переход от относительных единиц к абсолютным осуществляется по формулам:
; 
.
Если взаимосвязь факторов двух уровневая (n-уровневая), то необходимо рассчитывать коэффициент пропорционального деления для каждого уровня, а коэффициент долевого участия для каждого факторного показателя соответствующего уровня.
6. Интегральный способ
Для приемов элиминирования характерны следующие недостатки:
величина влияния фактора на изменение результативного показателя зависит от места расположения фактора в детерминированной модели;
дополнительный прирост результативного показателя, полученный от совместного взаимодействия факторов, присоединяется к последнему фактору.
Интегральный метод не имеет этих недостатков. Величина влияния фактора на изменение результативного показателя не зависит от места расположения фактора в детерминированной модели. Дополнительный прирост от совместного взаимодействия факторов, распределяется между ними поровну.
Метод применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях типа 
.
Для мультипликативных моделей:
Исходная модель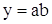 
.
; 
.
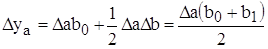
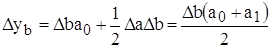
Исходная модель
; 
;
.
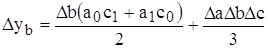
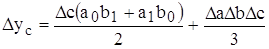
Исходная модель 
Кратная модель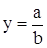 
; 
; 
.
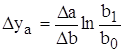
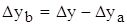
Смешанная модель типа: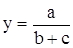 
; 
;
;
;
;
;
;
.
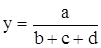
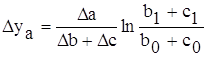
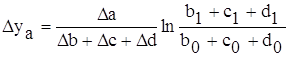
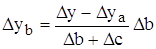
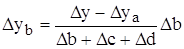
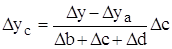
7. Способ логарифмирования
Применяется для измерения влияния факторов в мультипликативных моделях.
Результат расчета влияния факторов на результативный показатель при этом способе не зависит от места расположения факторов в модели. Дополнительный прирост от совместного взаимодействия факторов распределяется между ними пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя.
Исходная модель
; 
; 
.
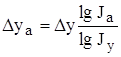
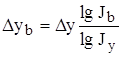
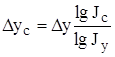
1. Экономика предприятия (фирмы): Учебник / Под. ред. проф. О.И.Волкова. – М.: ИНФРА-М, 2005. – 601 с.
2. Грузинов В.П., Грибов В.Д. Экономика предприятия: Учеб. пособие – М.: Финансы и статистика, 2005. – 208 с.
3. Сергеев И.В. Экономика предприятия. Учеб. пособие. – М.: Финансы и статистика, 2005. – 304 с.
4. Экономика предприятия / Под ред. Е.Л.Кантора. – СПб.: Питер, 2006. – 352 с.
Источник
Способы пропорционального деления и долевого участия
Способ пропорционального деления. Данный способ применяется для определения величины влияния факторов на изменение результативного показателя в аддитивных и смешанных моделях кратно-аддитивного типа:
Суть способа пропорционального деления состоит в том, что необходимо общее изменение результативного показателя распределить пропорционально влиянию каждого фактора.
Алгоритм расчета влияния факторов на изменение результативного показателя в аддитивных моделях включает следующие этапы:
1 этап. Построение факторной модели результативного показателя:
где у — результативный показатель;
а, b, с — факторные показатели, имеющие с результативным показателем аддитивную зависимость.
2 этап. Определение абсолютного изменения результативного показателя:
базисное значение результативного показателя:у0 = а0 + b0 + с0;
фактическое значение результативного показателя: у1 = а1 + b1 + c1
3 этап. Расчет влияния факторов на изменение результативного показателя:
4 этап. Проведение балансовой увязки полученных результатов:
∆ 
5 этап. Формулирование выводов по результатам проведенного анализа.
Таким образом, рассчитать влияние факторов в аддитивной факторной модели способом пропорционального деления можно следующим образом:
где ∆уXi— абсолютное изменение результативного показателя под влиянием хi-го фактора;
∆у — абсолютное изменение результативного показателя;
∆хi — абсолютное отклонение хi-го фактора, влияющего на изменение результативного показателя;
п — количество факторов, влияющих на изменение результативного показателя.
Способ долевого участия. Данный способ применяется для расчета влияния факторов в аддитивных и смешанных моделях кратно-аддитивного типа.
Суть способа долевого участия состоит в том, что необходимо определить долю влияния каждого фактора в общем изменении результативного показателя, которая затем умножается на общий прирост результативного показателя.
В аддитивной модели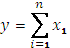 
расчет влияния факторов производится следующим образом:
Алгоритм расчета влияния факторов будет выглядеть следующим образом:
Источник
