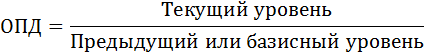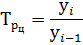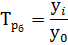Как рассчитать относительные величины динамики базисным способом

Статистика: Учебник / Под ред. Елисеевой.- М., 2006. С. 168-172

Оглавление

Показатели динамики (цепные и базисные)

Показатели динамики нашли широкое применения для формирования более наглядного представления о тенденции изменения уровней динамического ряда. Рост и снижение уровня ряда могут происходить либо равномерно, либо ускоренно, либо замедленно. Аналитические возможности показателей динамики раскрывает следующий фрагмент из учебника «Статистика»:

«Уровни временного ряда могут изменяться в самых разных, направлениях: они могут возрастать или убывать, повторять ранее достигнутый уровень. Интенсивность их изменения бывает различной. Уровни ряда могут изменяться быстрее или медленнее. Для характеристики развития явления во времени применяются следующие показатели:

• абсолютные приросты (_у);
• темпы роста (Т_р);
• темпы прироста (снижения) (Т_р);
• абсолютное ускорение или замедление ();
• относительное ускорение (Т_р).

Абсолютный прирост (абсолютное изменение) уровней ряда рассчи­тывается как разность двух уровней. Он показывает, на сколько единиц уровень одного периода больше или меньше уровня другого периода.

В зависимости от базы сравнения абсолютные приросты могут быть цепными и базисными:

Если каждый последующий уровень ряда динамики сравнивается со своим предыдущим уровнем, то прирост называется цепным. Если же в качестве базы сравнения выступает за ряд лет один и тот же период, то прирост называется базисным.

Один и тот же по величине абсолютный прирост может означать разную интенсивность изменения уровней (см. табл. 9.4).

Абсолютные приросты, тыс. шт.

Темпы роста, %

Темпы прироста, %

цепные

базисные

цепные

базисные

базисные

В нашем примере в 1996 и 1998 гг. абсолютное изменение объема продукции было одинаковым — 5 тыс. шт., но интенсивность рос­та объема произведенной продукции в эти годы была различной: в 1996 г. прирост в 5 тыс. ед. по сравнению с предыдущим годом составил 25%, а в 1998 г. по сравнению с предыдущим годом — лишь 14,3%. Аналогично один и тот же прирост в 10 тыс. ед. для 1997 и 1999 гг. означает разную интенсивность роста: в 1997 г. — прирост составил по сравнению с предыдущим годом, 40%, а в 1999 г. – 25%.

Интенсивность изменения уровней временного ряда характеризуется темпами роста и прироста.

Темп роста есть отношение двух уровней ряда. Как и абсолютные приросты, темпы роста могут рассчитываться как цепные и как базисные:

Если база сравнения по периодам меняется, то найденные темпы роста называются цепными. Если же база сравнения по периодам неизменна (y₀), то темпы роста называются базисными.

Темпы роста, выраженные в коэффициентах, принято называть коэффициентами роста:

В анализе используется один из этих показателей: либо темп роста, либо коэффициент роста, ибо экономическое их содержание одно и то же, но по-разному выражено: в % (Т_р) и в разах (К_р). Так по данным табл. 9.4 можно сделать вывод, что наибольшая интенсивность роста была достигнута в 1997 г., когда темп роста составил 140%, или в 1,4 раза превысил уровень предыдущего года.

Если цепные темпы роста характеризуют интенсивность изменения уровней от года к году (от месяца к месяцу), то базисные темпы роста фиксируют интенсивность роста, (снижения) за весь интервал времени между текущим и базисным уровнями. Так в примере базисный темп роста за весь период с 1996 по 1999 г. составил 250% (1995 г. взят за базу сравнения).

Темп прироста есть отношение абсолютного прироста к предыдущему уровню динамического ряда (цепной показатель) и к уровню, принятому за базу сравнения по динамическому ряду (базисный показатель):

По данным табл. 9.4, темп прироста для 1999 г. составит: цепной — 25% (·100) и базисный – 150% (·100), т.е. в 1999 г. объем продукции увеличился по сравнению с 1998 г. на 25%, а в целом за весь рассматриваемый период прирост составил 150%.

Между цепными и базисными показателями изменения уровней ряда существует следующая взаимосвязь:

• сумма цепных абсолютных приростов равна базисному приросту (см. табл. 9.4, где в итоговой строке накопленный прирост за 1996 — 1999 гг. – 30 тыс. шт. – совпадает с базисным абсолютным приростом для 1999 г.);
• произведение цепных коэффициентов роста равно базисному или равносильное этому деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентам роста. Так, по данным табл. 9.4, имеем:

, или 250% – базисный темп роста;

200/175=1,143, или 114,3% – цепной коэффициент роста для 1998 г. Взаимосвязь цепных и базисных темпов (коэффициентов) роста позволяет при анализе, если необходимо, переходить от цепных показателей к базисным и наоборот;

• темп прироста связан с темпом роста: (см. табл. 9.4, где темпы прироста меньше темпов роста на 100). Поэтому при анализе обычно приводится какой-то один из них: темп роста либо темп прироста. Зная цепные темпы прироста, можно определить базисный темп прироста. Для этого нужно от темпов прироста перейти к темпам (коэффициентам) роста и далее воспользоваться указанной выше взаимосвязью коэффициентов роста.

Так, например, изменение цен на потребительские товары и услуги за I квартал 2001 г. оказалось в Санкт-Петербурге следующим (см. гл. 9.5).

Изменение цен (в % к предыдущему месяцу)

В целом за I квартал прирост цен составит:

, т.е. в марте 2001 г. по сравнению с декабрем 2000 г. цены выросли на 7,4%.

Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за тот же промежуток времени:

или

Иными словами, абсолютное значение 1% прироста в данном периоде есть сотая часть достигнутого уровня в предыдущем периоде (см. табл. 9.4, последнюю графу). В связи с этим расчет абсолютного значения 1% прироста базисным методом не имеет смысла, ибо для каждого периода это будет одна и та же величина – сотая часть уровня базисного периода.

Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. Если они систематически возрастают, то ряд развивается с ускорением. Величина абсолютного ускорения определяется как т.е. по аналогии с цепным абсолютным приростом, но сравниваются между собой не уровни ряда, а их скорости. По табл. 9.4 в нашем примере ускорение имело место лишь в 1997 и в 1999 гг., когда =10-5=5 тыс. шт.

Если систематически растут цепные темпы роста, то ряд развивается с относительным ускорением. Относительное ускорение можно определить как разность следующих друг за другом темпов роста или прироста:

или

Полученная величина выражается в процентных пунктах (п.п.). По данным табл. 9.4, относительное ускорение имело место лишь в 1997 г.– 15 процентных пунктов по сравнению с предыдущим годом.

Относительное ускорение может быть измерено и с помощью коэффициента опережения.

Коэффициент опережения определяется как отношение последующего темпа роста к предыдущему:

В нашем примере коэффициент опережения для 1997 г. составил:

140/125=1,12, что означает, что в 1997 г. темп роста был в 1,12 раза больше, чем в 1996 г.

Коэффициенты опережения принято рассчитывать в сравнительном анализе нескольких рядов динамики. При параллельном изучении нескольких рядов динамики обычно их приводят к одному основанию путем расчета базисных темпов роста с одинаковой по времени базой сравнения для всех рядов. Это позволяет наглядно видеть, для какого ряда интенсивность изменения уровней наибольшая. Сравнивая далее наибольшие темпы роста с наименьшими, определяют коэффициенты опережения в развитии одного явления по отношению к другому (табл. 9.6).

Динамика доходов предприятия за 1-е полугодие 2004 г.(тыс. руб.)

Месяцы

Прибыль от реализации продукции

Прибыль от продажи прочих актов

Источник

Задача №18. Расчёт относительных показателей динамики

Имеются следующие данные о производстве одной из моделей iPhone компанией Apple за 2013 год:

Годы	Произведено продукция, тыс. шт.	Абсолютное значении 1 % прироста, тыс. шт.

I квартал	II квартал	III квартал	IV квартал
Произведено смартфонов, млн. штук	82,0	75,3	60,1	50,8

Определите относительные показатели динамики с переменной и постоянной базой сравнения. Проверьте их взаимосвязь.

Решение:

Относительная величина динамики характеризует развитие изучаемого явления во времени.

Относительный показатель динамики ( ОПД ) представляет собой отношение уровня изучаемого процесса или явления за данный период времени и уровня этого же процесса или явления в прошлом:

Относительный показатель динамики с переменной базой сравнения рассчитывается тогда, когда происходит сравнение с предыдущим уровнем. Его ещё также называют цепным темпом роста, так как основание относительной величины последовательно меняется. Темп роста может быть выражен в процентах или коэффициентах.

у_i – уровень текущего периода,

у_i-1 – уровень предшествующего периода.

Относительный показатель динамики с постоянной базой (базисный) рассчитывается тогда, когда происходит сравнение с одним и тем же базисным уровнем. Его ещё также называют базисным темпом роста. Темп роста может быть выражен в процентах или коэффициентах.

у₀ – уровень базисного периода.

I квартал	II квартал	III квартал	IV квартал
Произведено смартфонов, млн. штук	82,0	75,3	60,1	50,8
Темп роста базисный, %	100,0	91,8	73,3	62,0
Темп роста цепной, %	—	91,8	79,8	84,5

Из полученных базисных относительных величин динамики (темпов роста) видно, что за 2013 год объём производства смартфонов Apple неуклонно снижалось от квартала к кварталу:

Из полученных цепных относительных величин динамики (темпов роста) видно, что по отдельным этапам экономического развития также происходил спад производства.

Такое решение компании, возможно, вызвано тем, что спрос на устройства данной модели упал в связи с появлением новой более современной модели.

Между относительными показателями динамики с переменной и постоянной базой сравнения существует взаимосвязь: произведение цепных темпов роста (в коэффициентах) равно конечному базисному.

Источник

Относительная величина динамики

Относительны величины планового задания – это отношение предусмотренного планом уровня или объема к соответствующему фактически достигнутому уровню за предшествующий период, принятый за базу сравнения.

Относительные величины выполнения плана отражают степень выполнения плановых заданий и вычисляются как отношение фактически достигнутого уровня к плановому заданию.

Относительные величины динамики, планового задания и выполнения плана связаны между собой следующим соотношением: относительная величина динамики равна произведению относительных величин планового задания и выполнения плана.

С помощью относительных величин на основе различного рода сравнений обеспечивается оценка изучаемых свойств явлений, проводится анализ их значения и результатов развития.

Сравнение может проводиться во времени, в пространстве или с плановыми данными; может быть сравнение части и целого, отдельных частей целого между собой. Соответственно, различают следующие виды относительных величин.

Относительные величины структуры – это отношение части к целому. Они показывают, какой удельный вес (долю) составляет каждая часть совокупности в общей ее численности или в общем объеме изучаемого признака. Сумма относительных величин структуры изучаемой совокупности, выраженных в процентах, равна 100%, в долях – 1.

Относительные величины координации соотношение отдельных частей целого к одной из них, взятой за базу для сравнения. Такие показатели обеспечивают возможность анализировать пропорции между отдельными элементами совокупности, например соотношение в общем числе образовательных учреждений числа негосударственных и государственных учреждений, соотношение объема услуг и объема товаров в составе валового внутреннего продукта, соотношение собственных средств и обязательств в составе банковских ресурсов и др.

По официальным статистическим данным, абсолютные показатели по убийствам в США за период с 1980 по 2000 годы выглядит следующим образом:

Год	Количество убийств
1980	23040
1981	22520
1982	21010
1983	19310
1984	18690
1985	18980
1986	20610
1987	20100
1988	20680
1989	21500
1990	23440
1991	24700
1992	23760
1993	24530
1994	23330
1995	21610
1996	19650
1997	18210
1998	16914
1999	15522
2000	15517

Рассчитайте относительную величину динамики (ОВД) (абсолютный прирост, темпы роста и темпы прироста) базисным и цепным способами за 1996-2000 годы. Сделайте выводы.

Для решения воспользуемся сервисом «Показатели динамики».

Методика расчета
Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.
Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким способом показатели динамики называются цепными.
Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.
Абсолютный прирост
цепной прирост: ∆y_ц = y_i — y_i-1
базисный прирост: ∆y_б = y_i — y₁
Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.
Темп прироста
цепной темп прироста: T_прцi = ∆y_i / y_i-1
базисный темп прироста: T_пpб = ∆y_бi / y₁
Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Темп роста
цепной темп роста: T_pцi = y_i / y_i-1
базисный темп роста: T_pб = y_бi / y₁
Абсолютное значение 1% прироста
цепной: 1%_цi = y_i-1 / 100%
базисный: 1%_б = y_б / 100%
Темп наращения
Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала
T_н = ∆y_цi / y₁
Цепные показатели ряда динамики.

Период	Количество убийств	Абсолютный прирост	Темп прироста, %	Темпы роста, %	Абсолютное содержание 1% прироста	Темп наращения, %
1996	19650	0	0	100	196.5	0
1997	18210	-1440	-7.33	92.67	196.5	-7.33
1998	16914	-1296	-7.12	92.88	182.1	-6.6
1999	15522	-1392	-8.23	91.77	169.14	-7.08
2000	15517	-5	-0.0322	99.97	155.22	-0.0254
Итого	85813

В 2000 году по сравнению с 1999 годом количество убийств в США уменьшилось на 5 или на 0.0322%.
Минимальный прирост зафиксирован в 1997 году, когда число убийств сократилось на 1440.
Темп наращения показывает, что тенденция ряда возрастающая, что свидетельствует об ускорении снижения числа зарегистрированных убийств.

Базисные показатели ряда динамики.

Период	Количество убийств	Абсолютный прирост	Темп прироста, %	Темпы роста, %
1996	19650	0	0	100
1997	18210	-1440	-7.33	92.67
1998	16914	-2736	-13.92	86.08
1999	15522	-4128	-21.01	78.99
2000	15517	-4133	-21.03	78.97
Итого	85813

В 2000 году количество убийств составило 15517 и по сравнению с 1996 г. увеличилось на 4133, или на 21.03%.

Далее можно определить тенденцию ряда и построить аналитическое уравнение, по которому можно будет прогнозировать данные.

Источник