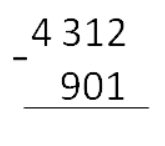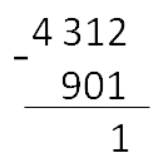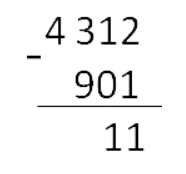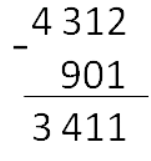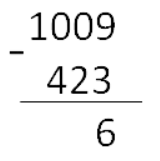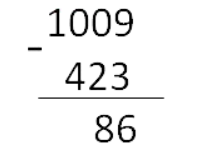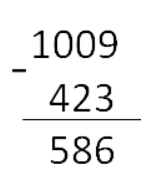- Математика. 2 класс
- Свойства сложения и вычитания
- Свойства сложения
- Свойства вычитания
- Примеры использования свойств сложения и вычитания
- Калькулятор суммы последовательных чисел
- Разложение чисел на составляющие
- Совершенные числа
- Последовательные числа
- Примеры
- Суммирование последовательных чисел
- Разложение чисел на сумму последовательных элементов
- Заключение
- Вычитание столбиком
- Основные понятия
- Свойства вычитания
- Алгоритм вычитания в столбик
Математика. 2 класс
Конспект урока
Математика, 2 класс. Урок №27
Проверка сложения. Проверка вычитания.
Перечень вопросов, рассматриваемых в теме:
— Что такое обратные математические действия?
— Как проверить сложение?
— Как проверить вычитание?
Глоссарий по теме:
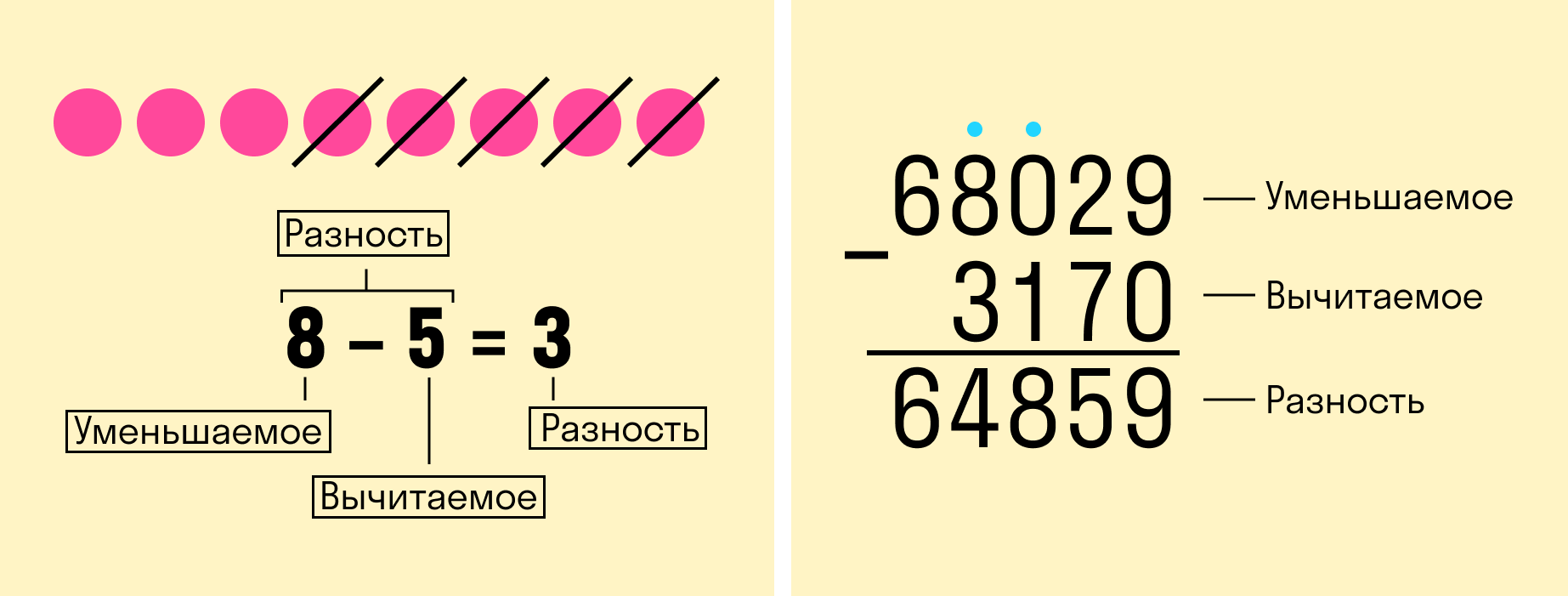
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых).
Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.
Обратные действия – действия, приводящие к прежнему, исходному состоянию.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. – 8-е изд. – М.: Просвещение, 2017. – с.84-86.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.60.
- Математика: переходим в 3-й класс. Учебное пособие для общеобразовательных организаций. А. В. Светин – М.: Просвещение: Уч. Лит, 2017. – с.40.
Теоретический материал для самостоятельного изучения
Используя числа 7, 5, 12 составим все возможные равенства.
7 + 5 = 12 12 – 5 = 7
12 – 7 = 5 5 + 7 = 12
Назовём компоненты и результат действия сложения.
Слагаемое + слагаемое = сумма
Назовём компоненты и результат действия вычитания.
Уменьшаемое – вычитаемое = разность
Действия сложение и вычитание связаны друг с другом, являются взаимно обратными действиями.
Как проверить, верно ли выполнено сложение. Воспользуемся знанием того, как связаны слагаемые и сумма. Если из суммы двух слагаемых вычесть одно из них, то получится другое слагаемое. Это позволяет сложение проверить вычитанием.
Например, надо проверить, верно ли вычислили сумму чисел 28 и 5. Для этого из суммы 33 вычтем одно из слагаемых. Например, 5. Должно получиться другое слагаемое. Получилось 28. Значит, сумма чисел 28 и 5 найдена правильно. Можно вычесть из суммы другое слагаемое.
Сумма чисел 36 и 9 найдена неверно, т.к. после вычитания из суммы 47 слагаемого 9, другое слагаемое, 36 не получается.
Вычислим ещё раз сумму чисел 36 и 9 и проверим результат.
36 – первое слагаемое
Сформулируем правило проверки сложения: «Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно».
Как проверить вычитание? Воспользуемся знанием того, как связаны между собой уменьшаемое, вычитаемое, разность. Если к разности прибавить вычитаемое, то получится уменьшаемое. Значит, вычитание можно проверить сложением.
Вычислим разность чисел 48 и 30. Она равна 18. Проверим вычитание сложением. К разности 18 прибавим вычитаемое 30, получим 48. Это уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
Значит, вычитание можно проверить и вычитанием. Рассмотрим это на примере.
Из уменьшаемого 48 вычтем разность 18, получим 30, т.е. вычитаемое. Значит, разность чисел 48 и 30 вычислена верно.
Сформулируем правила проверки вычитания: «Для проверки вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно», или «Для проверки вычитания, надо из уменьшаемого вычесть разность. Если в результате получается вычитаемое, значит, вычитание выполнено верно».
Вывод: Сложение и вычитание – это обратные действия. Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно. Для того, чтобы выполнить проверку вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно.
1. Найдите значение первого выражения в каждой рамке, а затем выполни проверку полученного результата двумя способами.
Источник
Свойства сложения и вычитания
О чем эта статья:
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
- 2 — это первое слагаемое,
- 5 — второе слагаемое,
- 7 — это сумма.
При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
- Переместительное свойство сложения
От перестановки мест слагаемых сумма не меняется.
a + b = b + a - Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c) - Свойство нуля при сложении
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
Рассмотрим пример 9 — 4 = 5, в котором:
При этом саму запись (9 — 4) тоже можно назвать разностью.

Примеры использования свойств сложения и вычитания
Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:
Пример 1
Вычислить сумму слагаемых с использованием разных свойств:
а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15
б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22
в) 30 + 0 + 13 = 30 + 13 = 43
Пример 2
Применить разные свойства при вычислении разности:
а) 25 — 0 — 2 = 25 — 2 = 23
б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13
Пример 3
Найти значение выражения удобным способом:
а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32
б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16
Источник
Калькулятор суммы последовательных чисел
Все числа характеризуются свойствами делимости или факторизации, но кроме этого существуют числа, которые легко представить в виде суммы последовательных натуральных чисел.
Разложение чисел на составляющие
В теории чисел каждое натуральное число легко представить в виде составляющих. Разложение элементов натурального множества на простые множители позволяет выразить числа в виде произведения составляющих. Простые множители — это элементы целого ряда, которые делятся только на себя и на единицу, но их произведение формирует искомое число. Например, 50 легко разбить на неделимые и записать его в виде 2 × 5 × 5. Однако числа можно представлять не только в виде произведения, но и в форме суммы.
Совершенные числа
Наиболее известным примером выражения натуральных чисел в виде суммы являются совершенные и последовательные числа. Совершенные числа представляют собой математические объекты, которые записываются в виде суммы собственных делителей. Например, к таким объектам относятся 6 и 28:
- при разложении 6 на делители получаем 1, 2 и 3, что в сумме дает 6;
- разложив 28 на делители, мы получим 1, 2, 4, 7, 14, что при сложении дает 28.
По мере того, как натуральный ряд растет, совершенные числа встречаются все реже. Первые шесть членов совершенной последовательности выглядят так:
6, 28, 496, 8 128, 33 550 336, 8 589 869 056.
Очевидно, что совершенных чисел не так много, а математикам до сих пор неизвестно, существуют ли их предел или совершенная последовательность устремляется в бесконечность.
Последовательные числа
Последовательные числа записываются в виде суммы последовательных членов натурального ряда. Натуральный ряд — это положительные целые числа, которые мы используем при счете предметов. Последовательные члены ряда — это два рядом стоящих элемента, к примеру, 2 и 3, 17 и 18, 178 и 179.
Достаточно много натуральных чисел мы можем записывать в виде суммы последовательных элементов. Например, число 57 мы можем записать в трех вариантах:
- 7 + 8 + 9 + 10 + 11 + 12 = 57;
- 18 + 19 + 20 = 57;
- 28 + 29 = 57.
Точно также легко записать 58, 59, 60 и далее, а вот 64 последовательным числом не является и его невозможно представить в виде суммы последовательных членов натурального ряда.
Наш онлайн-калькулятор позволяет представить натуральные числа в виде суммы последовательных. Как видно, выразить число в виде суммы можно несколькими способами, поэтому наша программа высчитывает только один способ, который раскладывает число на сумму наибольшего количества слагаемых.
Примеры
Суммирование последовательных чисел
В работе с последовательными элементами натурального ряда существует несколько хитростей. Первая из таких уловок — это сложение пяти последовательных чисел быстрым способом, который состоит в умножении на 5 третьего члена последовательности. Например, если мы хотим быстро сложить 1 + 2 + 3 + 4 + 5, нам достаточно умножить 3 на 5 и получить 15. Давайте проверим и введем 15 в форму онлайн-калькулятора:
15 = 1 + 2 + 3 + 4 + 5.
Если мы возьмем следующую сумму из пяти последовательных чисел, например, 10 + 11 + 12 + 13 + 14, то умножив третий член на 5, мы получим 12 × 5 = 60. Проверим число 60 на возможность разложения в последовательный ряд:
- 60 = 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11;
- 60 = 10 + 11 + 12 + 13 + 14;
- 60 = 19 + 20 + 21.
Как видите, число 60 легко разложить на сумму тремя способами, среди которых есть и наш, который выражен в виде суммы пяти последовательных чисел.
Разложение чисел на сумму последовательных элементов
Для решения такой задачи от вас потребуется только ввести число в форму калькулятора. Давайте попробуем разложить на последовательные слагаемые большие числа:
- 256 — не последовательное число;
- 404 = 47 + 48 + 49 + 50 + 51 + 52 + 53 + 54;
- 666 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 21 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 + 31 + 32 + 33 + 34 + 35 + 36.
Таким образом, вы можете разложить достаточно большое количество членов натурального ряда, так как не последовательные числа встречаются довольно редко.
Заключение
Теория чисел — чистая математика, которую трудно использовать в повседневной жизни. Несмотря на это, вы можете использовать нашу программу для исследования самых разных свойств чисел.
Источник
Вычитание столбиком
О чем эта статья:
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков. Однозначное — состоит из одного знака. Двузначное — из двух. Трехзначное — из трех и так далее.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.
- Разряд единиц — то, чем заканчивается любое число.
- Разряд десятков — то, что находится перед разрядом единиц.
- Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
Вычитание — это арифметическое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее — вычитаемым. Результат их вычитания — разностью.