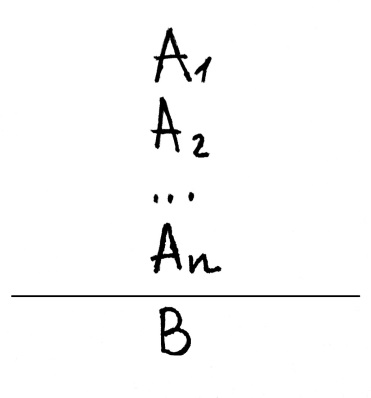Как проверить правильность умозаключения табличным способом

Прямые умозаключения логики высказываний

Умозаключения логики высказываний основаны на структуре сложных суждений (на смысле логических связок, объединяющих простые суждения в сложные) и не учитывают внутреннюю структуру простых суждений, входящих в посылки.

Умозаключения логики высказываний бывают прямые и непрямые. Прямыми называются умозаключения, в которых заключение выводится из некоторого множества суждений. Непрямыми являются умозаключения, которые получаются путём преобразования других умозаключений.

Виды простых[2] форм прямых умозаключений логики суждений:

1. Условно-категорические – это умозаключения, в которых одна посылка – условное суждение, а вторая посылка и заключение – суждения категорические. Условно-категорические умозаключения бывают двух разновидностей:

а) утверждающий модус: А®В, А В

б) отрицающий модус: А®В, щВ щА

(В схемах умозаключений над чертой записываются посылки, под чертой – заключение, черта означает «следовательно»; А и В – простые суждения).

Пример 1. Если человек простужен (А), то он болен (В).

Пример 2. Если человек простужен (А), то он болен (В).

Он не простужен (ùА).

Сходные схемы

А®В, В А

и

А®В, ùА ùВ

не являются правильными.

Пример 3. Из посылок «Если человек простужен (А), то он болен (В)» и «Человек болен (В)» вовсе не обязательно следует «Он простужен (А)». «Человек болен» может означать, что у него сломана нога, поднялось давление и т. п. И только с определенной долей вероятности может оказаться, что он болен, потому что простужен. Аналогично вероятным получится заключение и для отрицающего модуса.

2. Разделительно-категорические – это умозаключения, в которых одна посылка – разделительное суждение, а другая посылка и заключение – суждения категорические. Разделительно-категорические умозаключения также бывают двух разновидностей:

а) утверждающе-отрицающая схема:	б) отрицающе-утверждающая схема:
АЪВ, В щА	АЪВ, А щВ	АЪ (Ъ) В, щА В	АЪ (Ъ) В, щВ А

Пример. Отрицающе-утверждающая схема:

Либо мы уходим (А), либо мы остаемся (В).

3. Дилеммы (условно-разделительные силлогизмы) – это умозаключения, в которых две посылки – условные суждения, одна – разделительное, а заключение — либо простое суждение (в простой дилемме), либо сложное разделительное (дизъюнктивное) суждение (в сложной дилемме).

а) простая конструктивная дилемма:	б) простая деструктивная дилемма:
А®С, В®С АЪВ С	А®В, А®С щВЪщС щА
в) сложная конструктивная дилемма:	г) сложная деструктивная дилемма:
А®В, С®D AЪC BЪD	A®B, C®D щBЪщD щAЪщC

Пример. «Если вы будете говорить правду (А), люди проклянут вас (В), а если будете лгать (С), то вас проклянут боги (D). Но вы можете только говорить правду (A) или лгать (C). Значит, вас проклянут боги (D) или люди (B)». Если мы выпишем из этого рассуждения только буквенные обозначения простых суждений, соединив их соответствующими логическими связками, то получим форму сложной конструктивной дилеммы.

Имеется и еще одна форма дилемм – конструктивно-деструктивные, или деструктивно-конструктивные. В этих умозаключениях некоторые из членов разделительной посылки указывают на наличие оснований условных посылок, а некоторые – отрицают следствия (консеквенты) других условных посылок. Например, конструктивно-деструктивной является дилемма вида:

4. Чисто условные умозаключения – это вывод из любого количества посылок, которые представляют собой условные суждения и заключения которых также являются условными суждениями. К этим умозаключениям, в частности, относятся транзитивность импликации и правило контрапозиции.

а) транзитивность импликации:

Пример. «Если лобная кора головного мозга повреждена (A), то взаимодействие личности с внешней средой нарушается (B). В этом случае (B) человек утрачивает реальное восприятие действительности (C), а значит (C), превращается в раба ситуации (D)». Это умозаключение имеет форму транзитивности импликации с тремя посылками:

б) правило контрапозиции:

Пример. «Если человек знает геометрию (А), то он знает теорему Пифагора (В). Следовательно, если он не знает теоремы Пифагора (ùВ), то он не знает геометрии (ùА).

Все приведённые выше формы умозаключений являются правильными, то есть их соблюдение гарантирует правильность заключения при истинности посылок. Иногда эти формы называют правилами соответствующих умозаключений.

Для проверки правильности умозаключений, не сводимых к этим типам, используется, прежде всего, табличный метод. Он основан на том, что между посылками и заключением дедуктивного умозаключения должно существовать отношение логического следования, означающее, что заключение не может быть ложным, если все посылки истинны.

Чтобы проверить правильность умозаключения табличным способом, нужно составить формулу этого умозаключения. Для этого следует:

1) записать посылки и заключение на языке логики суждений;

2) соединить между собой посылки с помощью конъюнкции;

3) присоединить заключение к посылкам с помощью импликации;

4) для полученной формулы составить таблицу истинности.

Умозаключение будет правильным (гарантирующим истинность заключения при истинности посылок) только в том случае, если его формула является тождественно истинной (в последнем столбце таблицы все значения – «истина»).

Пример. «Если философ – дуалист, то он не материалист. Если он не материалист, то он диалектик или метафизик. Он не метафизик. Следовательно, он диалектик или дуалист».

Данное умозаключение довольно сложно привести к какому-либо традиционному типу, поэтому проверим его правильность табличным способом.

Запишем посылки и заключение нашего суждения на языке логики суждений. Обозначим: р – философ – дуалист; q – философ – материалист; r – философ – метафизик; s – философ – диалектик.

Тогда первая посылка – «Если философ – дуалист (р), то он не материалист (ùq)» – на языке логики суждений имеет вид:

Вторая посылка – «Если он не материалист (ùq), то он диалектик (s) или метафизик (r)» – запишется так:

Третья посылка – «Он не метафизик»:

Заключение – «Он диалектик (s) или дуалист (р)»:

Соединяя посылки конъюнкцией (Ù) и присоединяя к ним заключение импликацией (É), получаем формулу:

Для этой формулы составляем таблицу истинности:

p

q

r

s

ùq

ùr

A

B

C

D

E

F

(р®ùq)

sÚr

ùq®B

AÙC

DÙùr

sÚр

D®F

И

И

И

И

Л

Л

Л

И

И

Л

Л

И

И

Л

И

И

И

Л

Л

И

И

И

И

Л

И

И

И

Л

И

И

И

Л

И

И

И

И

Л

И

И

Л

Л

И

И

И

Л

И

И

И

И

Л

И

И

И

И

Л

И

Л

И

Л

И

И

Л

Л

И

И

Л

И

Л

И

Л

И

И

И

И

И

И

И

И

И

Л

Л

И

И

И

И

И

И

И

И

И

И

Л

Л

Л

И

И

И

И

И

И

И

И

И

И

И

И

И

Л

Л

Л

Л

И

И

Л

Л

И

И

Л

И

И

Л

Л

Л

И

И

И

И

Л

Л

Л

И

Л

И

Л

И

Л

И

И

И

И

Л

И

И

Л

Л

И

Л

И

Л

И

И

И

И

Л

Л

Л

И

И

Л

Л

Л

И

Л

Л

И

Л

Л

И

И

Л

И

Л

Л

Л

И

И

Л

И

И

И

Л

Л

И

Л

Л

Л

И

И

И

Л

Л

Л

Л

И

И

Л

Л

Л

Л

И

И

И

Л

Л

Л

Л

Л

И

Получилась выполнимая формула, так как последний столбец таблицы истинности содержит и значения «истина», и значения «ложь». Это говорит о том, что умозаключение вероятное.

При проверке правильности умозаключений можно не строить таблицу полностью, а, получив значения истинности посылок и заключения, ограничиваться рассмотрением только тех строк, в которых все посылки принимают значения «истина». Так, в данном примере, получив значения в столбцах 6 (третья посылка), 7 (первая посылка), 9 (вторая посылка) и 12 (заключение), мы могли бы исследовать только строки 6, 7, 8, 14.

Дело в том, что, с одной стороны, вести речь об истинности заключения имеет смысл только при условии истинности посылок. При ложных посылках даже правильное по форме умозаключение не может гарантировать истинности заключения. А, с другой стороны, проверяя правильность умозаключения, мы, по существу, проверяем, соблюдается ли в нем отношение логического следования между посылками и заключением. Оно как раз и состоит в том, что во всех случаях, когда посылки — истинные суждения, заключение — также истинное суждение, и ни в одной строке таблицы не наблюдается случая, когда все посылки истинны, а заключение ложно. При ложной же посылке мы вообще не можем говорить об отношении логического следования.

Источник

Урок 6. Умозаключения

В этом уроке мы, наконец, переходим к теме, которая составляет ядро любого рассуждения и любой логической системы – умозаключениям. В четвёртом уроке мы говорили, что рассуждение – это совокупность суждений или высказываний. Очевидно, что такое определение не полно, ведь оно ничего не говорит о том, почему вдруг какие-то разные высказывания оказались рядом. Если дать более точное определение, то рассуждение – это процесс обоснования какого-либо высказывания с помощью его последовательного вывода из других высказываний. Этот вывод чаще всего осуществляется в форме умозаключений.

Содержание:

Умозаключение – это непосредственный переход от одного или нескольких высказываний А₁, А₂, …, А_n к высказыванию В. А₁, А₂, …, А_n называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.

В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:

Перебрав в уме еще раз показания пассажиров, я пришел к весьма любопытным результатам. Для начала возьмем показания мистера Маккуина. Первая беседа с ним не вызвала у меня никаких подозрений. Но во время второй он обронил небезынтересную фразу. Я сообщил ему, что мы нашли записку, в которой упоминается о деле Армстронгов. Он сказал: «А разве…» – осекся и, помолчав, добавил: «Ну это самое… неужели старик поступил так опрометчиво?…»

Но я почувствовал, что он перестроился на ходу. Предположим, он хотел сказать: «А разве ее не сожгли?» Следовательно, Маккуин знал и о записке, и о том, что ее сожгли, или, говоря другими словами, он был убийцей или пособником убийцы.

Логики записывают умозаключения следующим образом:

Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.

Критерии истинности умозаключений

Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.

Второй аспект – это правильность самого умозаключения с точки зрения его логической формы. Дело в том, что истинность посылок – это важное, но недостаточное условие для того, чтобы заключение было правильным. Нередки ситуации, когда посылки истинны, но заключение неверно. В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:

Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.

Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.

Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.

Умозаключения по логическому квадрату

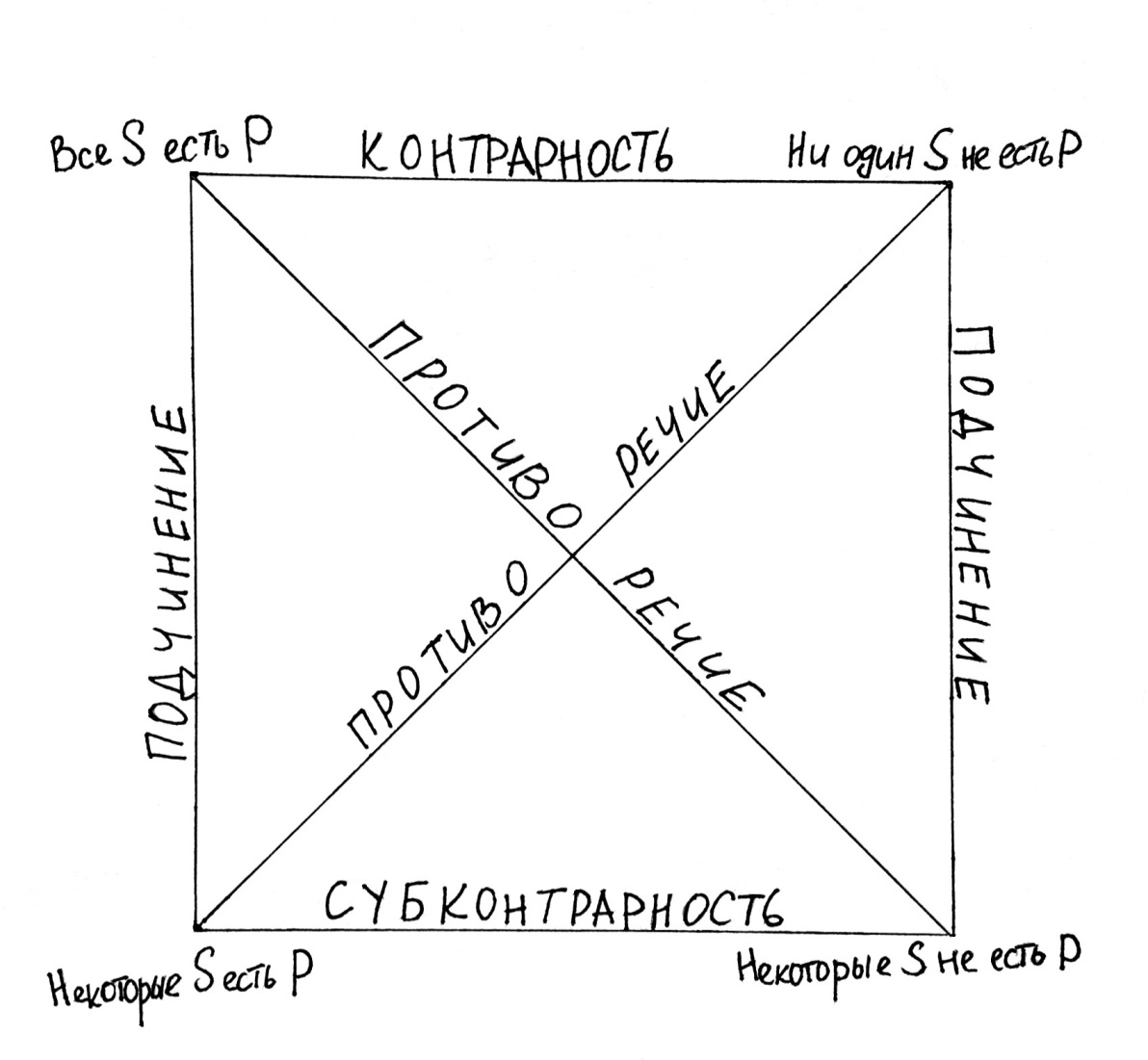
Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:

Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:

• Все S есть P
• Некоторые S есть P
• Все птицы имеют клюв. Следовательно, некоторые птицы имеют клюв.
• Ни один S не есть P
• Некоторые S не есть P
• Ни один гусь не хочет быть пойман и зажарен. Следовательно, некоторые гуси не хотят быть пойманными и зажаренными.

Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:

• Неверно, что некоторые S есть P
• Неверно, что все S есть P
• Неверно, что некоторые автомобили не имеют колёс. Поэтому неверно, что все автомобили не имеют колёс.
• Неверно, что некоторые S не есть P
• Неверно, что все S не есть P
• Неверно, что некоторые вина не являются спиртными напитками. Таким образом, неверно, что все вина не являются спиртными напитками.

Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.

По закону контрарного противоречия будут истинными следующие виды умозаключений:

• Все S есть P
• Неверно, что ни один S не есть P
• Все яблоки – это фрукты. Следовательно, неверно, что ни одно яблоко не является фруктом.
• Ни один S не есть P
• Неверно, что все S есть P
• Ни один кит не умеет летать. Поэтому неверно, что все киты умеют летать.

Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.

• Согласно этому закону правильными будут следующие умозаключения:
• Неверно, что некоторые S есть P
• Некоторые S не есть P
• Неверно, что некоторые продукты полезны для здоровья. Поэтому некоторые продукты не полезны для здоровья.
• Неверно, что некоторые S не есть P
• Некоторые S есть P
• Неверно, что некоторые ученики из нашего класса не являются двоечниками. Таким образом, некоторые ученики из нашего класса являются двоечниками.

Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.

На этих законах строятся умозаключения следующих видов:

• Все S есть P
• Неверно, что некоторые S не есть P
• Все дети нуждаются в заботе. Следовательно, неверно, что некоторые дети не нуждаются в заботе.
• Некоторые S не есть P
• Неверно, что все S есть P
• Некоторые книги не являются скучными. Поэтому, неверно, что все книги являются скучными.
• Неверно, что все S есть P
• Некоторые S не есть P
• Неверно, что все сотрудники нашей фирмы усердно работают. Таким образом, некоторые сотрудники нашей фирмы не работают усердно.
• Неверно, что некоторые S не есть P
• Все S есть P
• Неверно, что некоторые зебры не имеют полосок на коже. Следовательно, все зебры имеют полоски на коже.
• Ни один S не есть P
• Неверно, что некоторые S есть P
• Ни одна картина в этом зале не относится к XX веку. Поэтому неверно, что некоторые картины в этом зале относятся к XX веку.
• Некоторые S есть P
• Неверно, что ни один S не есть P
• Некоторые студенты занимаются спортом. Таким образом, неверно, что ни один студент не занимается спортом.
• Неверно, что ни один S не есть P
• Некоторые S есть P
• Неверно, что ни один учёный не интересуется искусством. Следовательно, некоторые учёные интересуются искусством.
• Неверно, что некоторые S есть P
• Ни один S не есть P
• Неверно, что некоторые коты курят сигары. Таким образом, ни один кот не курит сигары.

Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.

Операция обращения

Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.

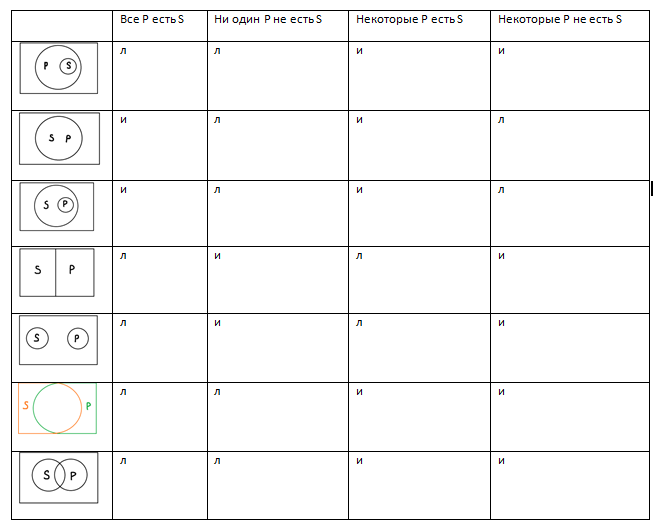
Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.

Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.

Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:

• Ни один S не есть P
• Ни один P не есть S
• Ни один человек не может выжить без воздуха. Следовательно, ни одно живое существо, способное выжить без воздуха, не является человеком.
• Некоторые S есть P
• Некоторые P есть S
• Некоторые змеи ядовиты. Поэтому, некоторые ядовитые существа – это змеи.
• Для высказываний типа «Все S есть P» и «Ни один S не есть P» верно обращение с ограничением:
• Все S есть P
• Некоторые P есть S
• Все пингвины – это птицы. Таким образом, некоторые птицы – это пингвины.
• Ни один S не есть P
• Некоторый P не есть S
• Ни один крокодил не ест зефир. Следовательно, некоторые существа, едящие зефир, не являются крокодилами.
• Высказывания типа «Некоторые S не есть P» вообще не обращаются.

Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.

Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.

Упражнение «Подберите ключ»

В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Упражнения

Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:

• Все медведи на зиму залегают в спячку.
• Неверно, что все люди завистливы.
• Ни один гном не достигает роста в два метра.
• Неверно, что ни один человек не был на Северном полюсе.
• Некоторые люди никогда не видели снега.
• Некоторые автобусы ходят по расписанию.
• Неверно, что некоторые слоны летали на луну.
• Неверно, что некоторые птицы не имеют крыльев.

Сделайте обращения с теми, высказываниями, с которыми это возможно:

• Никто ещё не построил машину времени.
• Некоторые официанты очень назойливы.
• Все профессионалы опытны в своём деле.
• Некоторые книги не имеют твёрдой обложки.

Проверьте, правильно ли сделаны следующие умозаключения:

• Некоторые кролики не носят белые перчатки. Следовательно, некоторые кролики носят белые перчатки.
• Неверно, что никто не был на Луне. Таким образом, некоторые люди были на Луне.
• Все люди смертны. Поэтому все смертные – это люди.
• Некоторые птицы не умеют летать. Следовательно, некоторые существа, не умеющие летать, это птицы.
• Ни один ягнёнок не имеет пристрастия к виски. Следовательно, ни одно существо, имеющее пристрастие к виски, не является ягнёнком.
• Некоторые морские животные млекопитающие. Таким образом, неверно, что ни одно морское животное не является млекопитающим.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Источник