Глава 9. Преобразование комплексных чертежей

§ 59. Способ вращения

Как уже отмечалось, при преобразовании комплексного чертежа возможно изменение положения заданных геометрических элементов относительно плоскостей проекций при неизменном положении основных плоскостей проекций. Это осуществляется путем вращения этих элементов вокруг некоторой оси до тех пор, пока эти элементы не займут частное положение в исходной системе плоскостей. Такое преобразование комплексного чертежа носит название способа вращения .

В качестве оси вращения в этом случае удобнее всего выбирать проецирующие прямые или прямые уровня, тогда точка будет вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций.

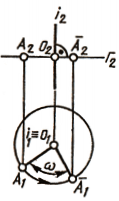
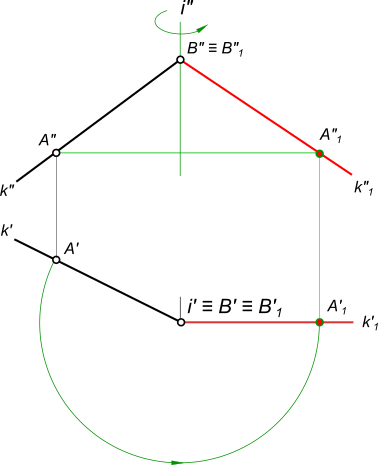
При вращении вокруг горизонтально проецирующей прямой горизонтальная проекция А₁ точки А перемещается по окружности, а фронтальная А₂ — по прямой, перпендикулярной фронтальной проекции оси, являющейся фронтальной проекцией плоскости вращения Г₂ (рис. 115).

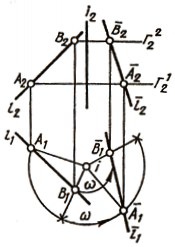
При этом расстояние между горизонтальными проекциями двух точек А и В (рис. 116) при их повороте на один и тот же угол остается неизменным (A₁B₁ = A ₁ B ₁).

Аналогичные выводы можно сделать и для вращения вокруг фронтально проецирующей прямой. При вращении плоской фигуры вокруг оси, перпендикулярной плоскости проекций, проекция ее на эту плоскость не изменяется ни по величине, ни по форме, так как не изменяется наклон плоской фигуры к этой плоскости, а меняется лишь положение этой проекции относительно линии связи. Вторая же проекция на плоскости, параллельной оси вращения, изменяется и по форме, и по величине. Проекции точек на этой плоскости проекций находятся на прямых, перпендикулярных исходным линиям связи. Пользуясь этими свойствами, можно применить для преобразования чертежа способ вращения, не задаваясь изображением оси вращения и не устанавливая величину радиуса вращения. Это — способ плоскопараллельного перемещения , при котором все точки геометрической фигуры перемещаются во взаимно параллельных плоскостях без изменения действительного вида и размеров этой фигуры (рис. 117).

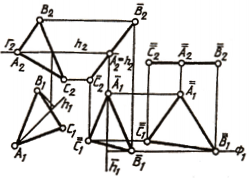
Треугольник ABC занимает общее положение. Первым плоскопараллельным перемещением он поставлен во фронтально проецирующее положение с помощью горизонтали h, которую расположим как фронтально проецирующующмшую в ее плоскости вращения Г ׀׀ П. При этом A₁B₁C₁ = ∆ A ₁ B ₁ C ₁, а плоскости вращения точек В и С параллельны плоскости Г.

Вторым перемещением ∆АВС расположен параллельно плоскости П₁. Без изменения оставлена вырожденная фронтальная проекция треугольника ( А ₂ В ₂ С ₂ = А ₂ В ₂ С ₂), а новая горизонтальная проекция, дающая истинную величину ∆АВС поручена построением новых горизонтальных проекций точек A ₁, B ₁ и С ₁ в результате их вращения в параллельных фронтальных плоскостях уровня ( В ₂ ∈ Ф; В ∈ Ф).

На этом примере построено решение третьей и четвертой исходных задач путем преобразования комплексного чертежа плоскости общего положения способом плоскопараллельного перемещения.

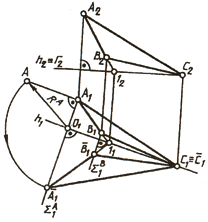
Если в качестве оси вращения взять линию уровня, то истинную величину плоской фигуры общего положения можно построить одним поворотом, т.е. избежать двойного преобразования чертежа, что имело место в замене плоскостей проекций и плос-копараллельномперемещении. На рис. 118 построено изображение ∆АВС ( A ₁ B ₁ C ₁) после поворота его вокруг горизонтали h(C, 1) уровня Г ∈ h.

Так как горизонталь проходит через точку С, то последняя неподвижна при вращении треугольника. Нужно повернуть только точки А и В вокруг горизонтали до совмещения с плоскостью Г ׀׀ П₁. Точка А вращается в горизонтально проецирующей плоскости Σ A , перпендикулярной оси вращения. Центр вращения 0 точки А лежит на оси вращения. В момент, когда в результате вращения точка А окажется в плоскости Г, т. е. совместится с горизонтальной плоскостью уровня, ее горизонтальная проекция A ₁ будет удалена от горизонтальной проекции оси вращения h₁ на расстояние, равное истинной величине радиуса вращения R A точки А. Натуральную величину R A можно построить как гипотенузу О₁А прямоугольного треугольника (см. § 42), одним катетом которого является горизонтальная проекция радиуса А₁О₁, а вторым — разность высот точек А и О. Построив совмещенную горизонтальную проекцию точки А, легко достроить изображение всего треугольника А₁В₁С₁ в совмещенном с плоскостью /положении, используя неподвижную точку и плоскость вращения точки В (Σ₁ B ⊥ h₁). Фронтальная проекция ∆АВС выродится в прямую и совместится с проекцией Г₂ плоскости совмещения.

Аналогичные действия выполняют при вращении плоской фигуры вокруг ее фронтали. Совмещение в этом случае ведется с фронтальной плоскостью уровня (Ф ׀׀ П₂), проходящей через ось вращения — фронталь.

Способом вращения могут быть решены и другие задачи, применительно к их условиям.

© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения

Источник

Глава 9. Преобразование комплексных чертежей

§ 59. Способ вращения

Как уже отмечалось, при преобразовании комплексного чертежа возможно изменение положения заданных геометрических элементов относительно плоскостей проекций при неизменном положении основных плоскостей проекций. Это осуществляется путем вращения этих элементов вокруг некоторой оси до тех пор, пока эти элементы не займут частное положение в исходной системе плоскостей. Такое преобразование комплексного чертежа носит название способа вращения .

В качестве оси вращения в этом случае удобнее всего выбирать проецирующие прямые или прямые уровня, тогда точка будет вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций.

При вращении вокруг горизонтально проецирующей прямой горизонтальная проекция А₁ точки А перемещается по окружности, а фронтальная А₂ — по прямой, перпендикулярной фронтальной проекции оси, являющейся фронтальной проекцией плоскости вращения Г₂ (рис. 115).

При этом расстояние между горизонтальными проекциями двух точек А и В (рис. 116) при их повороте на один и тот же угол остается неизменным (A₁B₁ = A ₁ B ₁).

Аналогичные выводы можно сделать и для вращения вокруг фронтально проецирующей прямой. При вращении плоской фигуры вокруг оси, перпендикулярной плоскости проекций, проекция ее на эту плоскость не изменяется ни по величине, ни по форме, так как не изменяется наклон плоской фигуры к этой плоскости, а меняется лишь положение этой проекции относительно линии связи. Вторая же проекция на плоскости, параллельной оси вращения, изменяется и по форме, и по величине. Проекции точек на этой плоскости проекций находятся на прямых, перпендикулярных исходным линиям связи. Пользуясь этими свойствами, можно применить для преобразования чертежа способ вращения, не задаваясь изображением оси вращения и не устанавливая величину радиуса вращения. Это — способ плоскопараллельного перемещения , при котором все точки геометрической фигуры перемещаются во взаимно параллельных плоскостях без изменения действительного вида и размеров этой фигуры (рис. 117).

Треугольник ABC занимает общее положение. Первым плоскопараллельным перемещением он поставлен во фронтально проецирующее положение с помощью горизонтали h, которую расположим как фронтально проецирующующмшую в ее плоскости вращения Г ׀׀ П. При этом A₁B₁C₁ = ∆ A ₁ B ₁ C ₁, а плоскости вращения точек В и С параллельны плоскости Г.

Вторым перемещением ∆АВС расположен параллельно плоскости П₁. Без изменения оставлена вырожденная фронтальная проекция треугольника ( А ₂ В ₂ С ₂ = А ₂ В ₂ С ₂), а новая горизонтальная проекция, дающая истинную величину ∆АВС поручена построением новых горизонтальных проекций точек A ₁, B ₁ и С ₁ в результате их вращения в параллельных фронтальных плоскостях уровня ( В ₂ ∈ Ф; В ∈ Ф).

На этом примере построено решение третьей и четвертой исходных задач путем преобразования комплексного чертежа плоскости общего положения способом плоскопараллельного перемещения.

Если в качестве оси вращения взять линию уровня, то истинную величину плоской фигуры общего положения можно построить одним поворотом, т.е. избежать двойного преобразования чертежа, что имело место в замене плоскостей проекций и плос-копараллельномперемещении. На рис. 118 построено изображение ∆АВС ( A ₁ B ₁ C ₁) после поворота его вокруг горизонтали h(C, 1) уровня Г ∈ h.

Так как горизонталь проходит через точку С, то последняя неподвижна при вращении треугольника. Нужно повернуть только точки А и В вокруг горизонтали до совмещения с плоскостью Г ׀׀ П₁. Точка А вращается в горизонтально проецирующей плоскости Σ A , перпендикулярной оси вращения. Центр вращения 0 точки А лежит на оси вращения. В момент, когда в результате вращения точка А окажется в плоскости Г, т. е. совместится с горизонтальной плоскостью уровня, ее горизонтальная проекция A ₁ будет удалена от горизонтальной проекции оси вращения h₁ на расстояние, равное истинной величине радиуса вращения R A точки А. Натуральную величину R A можно построить как гипотенузу О₁А прямоугольного треугольника (см. § 42), одним катетом которого является горизонтальная проекция радиуса А₁О₁, а вторым — разность высот точек А и О. Построив совмещенную горизонтальную проекцию точки А, легко достроить изображение всего треугольника А₁В₁С₁ в совмещенном с плоскостью /положении, используя неподвижную точку и плоскость вращения точки В (Σ₁ B ⊥ h₁). Фронтальная проекция ∆АВС выродится в прямую и совместится с проекцией Г₂ плоскости совмещения.

Аналогичные действия выполняют при вращении плоской фигуры вокруг ее фронтали. Совмещение в этом случае ведется с фронтальной плоскостью уровня (Ф ׀׀ П₂), проходящей через ось вращения — фронталь.

Способом вращения могут быть решены и другие задачи, применительно к их условиям.

© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения

Источник

Способ вращения

Вращение вокруг оси, перпендикулярной плоскости проекции, является частным случаем параллельного перемещения. Отличие от параллельного перемещения состоит лишь в том, что за траекторию перемещения точки берется не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между точкой и осью вращения.

Способ вращения вокруг оси, перпендикулярной плоскости проекции, применим для перемещения отрезка прямой общего положения в частное.

Перевод прямой общего положения k в положение перпендикулярное горизонтальной плоскости проекции H.

Здесь необходимо дважды применить способ вращения вокруг осей, перпендикулярных к плоскостям проекции. Первым вращением отрезок переводится в положение, параллельное плоскости проекции V, и лишь после этого вращением вокруг оси перпендикулярной плоскости проекции V, перемещают отрезок в положение, перпендикулярное плоскости H .

Перевод плоскости общего положения в частное фронтально проецирующее положение.

Прямую, принадлежащую плоскости произвольно расположенной в пространстве, используя способ вращения переводим в положение перпендикулярное плоскости V. Используем для этого горизонталь плоскости, заданную точками 1 и 2 на рисунке.

Используем способ вращения напоследок, для придания плоскости положения параллельного плоскости проекции H, то есть положения плоскости уровня. Используем для этого ось вращения i₁.

Источник

Метод вращения вокруг оси

Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.

Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

1. Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
2. При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
3. При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’₁ так, чтобы выполнялось условие C’₁D’₁ || X. Для нахождения точки C»₁ из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’₁.

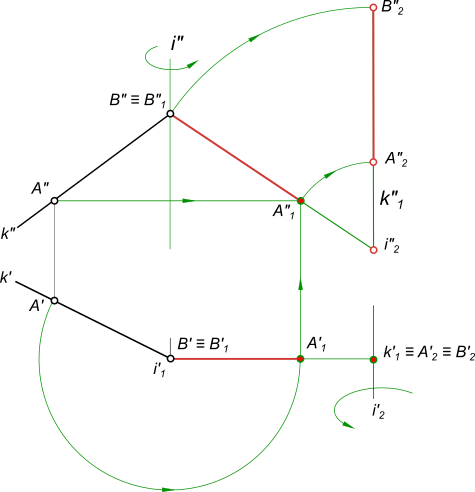
На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁ CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂ отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁ проходит через точку D, а проекция i»₂ фронтально проецирующей прямой i₂ лежит на продолжении отрезка C»₁D»₁.

Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

1. Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
2. При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
3. При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f». Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

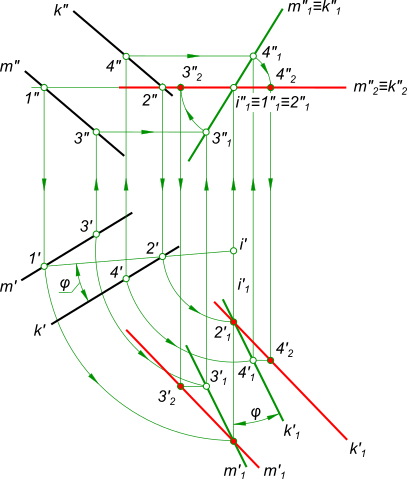
Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

1. Проводим фронтальную проекцию h» горизонтали h. Она пересекает прямые a» и b» в точках 1» и 2». Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
2. Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
3. Определяем натуральную величину радиуса вращения R = O’A’₀. Для этого строим прямоугольный треугольник O’A’A’₀, катет которого A’A’₀ равен расстоянию от A» до h».
4. Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’₁. Соединяем A’₁ с точками 1′ и 2′. Искомый угол ϕ построен.

Источник