Математика
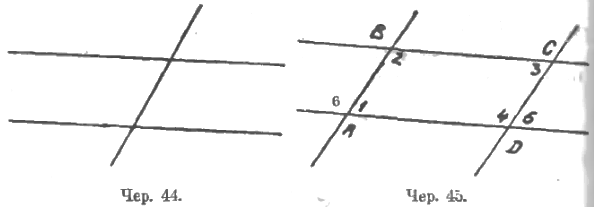
Построение параллельных прямых дает нам 3 прямых: 2 параллельных и одну секущую (чер. 44).
Возникает мысль усложнить фигуру: построить еще 4-ую прямую, параллельную секущей, – получим параллелограмм (чер. 45).
Учащиеся должны практиковаться и в построении и в рисовании от руки параллелограммов различной формы.
Изучаем полученную фигуру (параллелограмм). Сначала обращаем внимание на углы. Учащиеся должны видеть, что ∠1 = ∠3 (при помощи ∠5), что ∠2 = ∠4 (при помощи, напр. ∠6), что ∠1 + ∠2 = выпрямл. углу, ∠1 + ∠4 = выпрямл. углу и т. д.
У параллелограмма 4 вершины и 4 стороны, на каждой прямой определяется отрезок, который также называется стороною. Если обращаем внимание только на эти отрезки и на внутренние углы (внутри которых лежит площадь параллелограмма), то удобно изображать параллелограммы в виде (чер. 46).
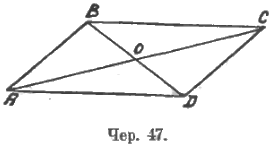
Дальнейшее изучение параллелограммов начинается с соображения: у параллелограмма 4 вершины, сколько прямых определяется этими четырьмя точками? (Аналогичный жизненный вопрос: четверо встретились и обменялись рукопожатиями, сколько вышло рукопожатий?). Когда выяснится, что 6 прямых, то надо построить 2 недостающих. Получим фигуру, изображенную на чер. 47.
Получились знакомые фигуры – треугольники. На вопрос, сколько здесь вы видите треугольников, учащиеся часто отвечают: «4». И только некоторые, более наблюдательные, видят здесь больше 4-х треугольников. Наконец, выясняется, что здесь 8 треугольников: 4 «больших» и 4 «малых». Обращаем внимание сначала на «большие» и ставим вопрос: нет ли среди них равных? Учащиеся, нарисовав от руки несколько различных параллелограммов, подмечают непосредственно, что вероятно соседние большие треугольники равны (ABD и DBC). Выясняется справедливость или несправедливость этого «подозрения». Оказывается, что в ∆ABD и ∆DBC общая сторона BD и заведомо равны попарно углы, к ней прилежащие, – этого достаточно, чтобы быть убежденным в равенстве треугольников. Отсюда получаем свойство параллелограмма, что его противоположные стороны равны.
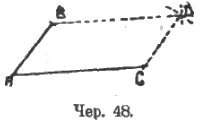
Это свойство зарождает мысль о новом, более удобном построении параллелограмма (чер. 48). Строим произвольно 3 вершины параллелограмма – A, B и C – и строим заранее 2 его стороны AB и AC. Остается найти четвертую вершину. Так как сторона, идущая из B ║ AC, должна быть равна AC, то строим, принимая B за центр и AC за радиус, круг (или только дугу); также, принимая C за центр и AB за радиус, строим другой круг (или дугу). Из двух точек пересечения кругов выберем ту, чтобы, после соединения ее с B и C, выделился один кусок плоскости.
Пусть эта точка есть точка D. Тогда, соединив ее с B и C, получим параллелограмм. Само построение, в соединении со свойством сторон параллелограмма, дает уверенность в том, что действительно получился параллелограмм. Однако, возможно сделать и проверку. Последняя ясна из следующей схемы:
Мы знаем: 1) BD = AC, 2) CD = AB (так строили).
Параллельны ли между собою BD и AC? А также CD и AB? Построив диагональ BC и рассмотрев полученные треугольники, приходим к утвердительному ответу на поставленный вопрос.
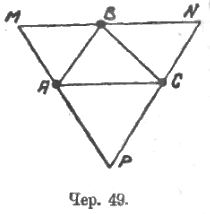
Очень интересно поставить на очередь общую задачу: «построить параллелограмм по трем данным вершинам» (чер. 49). Эта задача имеет 3 решения. Получаемая фигура дает возможность видеть: 1) можно получить треугольники (∆MNP и ∆ABC или ∆AMB), чтобы стороны одного были в 2 раза каждая больше стороны другого, – в таком случае площадь одного в 4 раза больше площади другого; 2) можно видеть свойства средней линии треугольника. Исследование (и построение) этой фигуры является интересным для учащихся материалом целого урока.
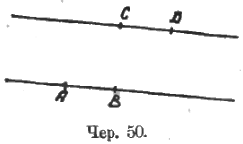
Очень хорошо также (это нужно для дальнейшего) сообщить учащимся и такой способ построения параллелограмма (чер. 50): строим 2 параллельных прямых, на них 2 равных отрезка и концы этих отрезков соединяем так, чтобы выделить определенную площадь.
Переходим с учащимися, затем к рассмотрению малых треугольников, получаемых у параллелограмма.
Здесь мы впервые встречаемся со случаем деления отрезка пополам. Когда учащиеся это увидят, то для них возникнет задача: разделить данный отрезок пополам.
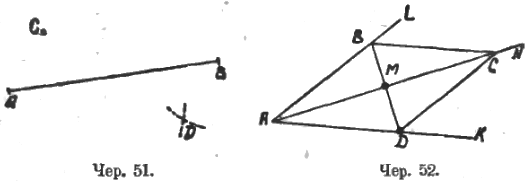
Решение этой задачи основывается на соображении (чер. 51): данный отрезок AB должен представлять собою диагональ параллелограмма; две противоположные вершины этого параллелограмма суть A и B; третью вершину C возьмем произвольно и построим при помощи кругов четвертую вершину D (чтобы AD = CB и BD = AC). Тогда диагональ CD должна разделить пополам диагональ AB.
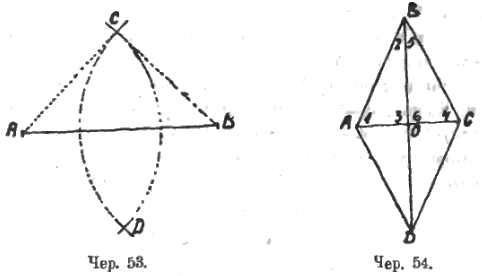
Более внимательное изучение параллелограмма (однако, его очень трудно провести с учащимися, лишь начинающими учиться геометрии, и предпочтительнее отложить на дополнительный курс) позволит увидеть происхождение (а, следовательно, и решение) задач (чер. 52): 1) дан угол (∠KAL) и точка внутри его (точка M) – построить через эту точку прямую так, чтобы ее отрезок между сторонами угла делился в этой точке пополам. 2) Дан угол (∠LAN) и точка вне его (точ. D); построить через эту точку прямую так, чтобы ее отрезок, заключенный между сторонами угла, равнялся отрезку от этой точки до ближайшей стороны угла.
Упражнения в делении отрезка пополам приводят к мысли о возможности упрощения этого построения: приходится строить 2 круга разными радиусами, – нельзя ли пристроить к данному отрезку параллелограмм только при помощи одного растворения циркуля? Ответ на этот вопрос приводит к особенному параллелограмму (ромб), у которого все стороны равны (чер. 53).
Заметим также, что упражнения в делении отрезка пополам должно вести так, чтобы стороны параллелограмма (или ромба), пристраиваемого к отрезку, не рисовались учащимися, а лишь показывались, а начертить необходимо лишь вторую диагональ.
Раз получен особый параллелограмм – ромб (чер. 54), то возникает вопрос, нет ли у него особенностей, как-либо отличающих его от обычного параллелограмма. Учащиеся подмечают, что, вероятно, у ромба все 4 маленьких треугольника равны. Следует выяснить, что новым в этом предварительном наблюдении является лишь равенство соседних маленьких треугольников (противоположные ведь равны у всякого параллелограмма). Делаем проверку: действительно оказывается, напр. у ∆AOB и ∆OBC, что их стороны заведомо попарно равны. Предварительно наблюдение оправдалось. Отсюда заключаем, что и углы у этих соседних треугольников попарно равны: 1) ∠1 = ∠4, но это равенство ничего нового не дает, так как оно выражает знакомое свойство углов при основании в равнобедренном треугольнике (∆ABC равнобедренный). 2) ∠2 = ∠5. Это обстоятельство дает нечто новое: ∠ABC («весь» ∠B) ромба разделился пополам. Отсюда возникает задача: дан какой-нибудь угол; разделить его пополам. Решение задачи ясно из сравнения данного угла с ромбом: надо к данному углу пристроить ромб так, чтобы вершина угла служила бы одною вершиною ромба и чтобы две стороны ромба шли по сторонам данного угла. Таких ромбов пристроить к углу можно сколь-угодно много, и они будут отличаться друг от друга размерами своих сторон. Взяв за сторону ромба произвольный отрезок (определяемый концами раздвинутых ножек циркуля, подготовленного к построению ромба), мы этот ромб легко пристроим к углу: сначала на сторонах угла определяем еще 2 вершины ромба и, наконец, построением соответствующих дуг определяем и 4-ую вершину; сторон ромба строить нет надобности (но учащиеся должны их показывать), а надо построить ту его диагональ, которая идет из вершины данного угла. 3) ∠3 = ∠6 (продолжаем изучать соседние малые треугольники). Это равенство также дает новое, а именно: мы видим, что выпрямленный ∠AOC разделился пополам. Вводим термины «прямой» угол (половина выпрямленного угла) и «перпендикулярные» прямые. Является возможность поставить на очередь задачи: 1) построить прямой угол и 2) построить 2 перпендикулярных прямых. Последняя задача развертывается в две: 1) дана прямая и точка на ней, построить через эту точку перпендикуляр к данной прямой и 2) дана прямая и точка вне ее; построить через эту точку перпендикуляр к данной прямой. Подробности того, как провести эти построения с учащимися, пропускаем, так как в них легко ориентироваться в связи с тем, что было дано здесь по поводу предыдущих построений.
Раз получен еще особый угол, прямой, то возникает потребность строить особые и треугольники и параллелограммы, а именно – с прямыми углами. Здесь является возможным более подробное изучение прямоугольных треугольников: 1) как упрощаются общие признаки равенства для прямоугольных треугольников, 2) какие еще признаки равенства удобно ввести для прямоугольных треугольников.
Построив параллелограмм так, чтобы у него один угол был прямой, мы приходим к заключению, что все его углы прямые и переходим к изучению прямоугольники (все 4 «больших» треугольника равны), а затем и квадрата.
Соединение понятия о прямом угле с равносторонним треугольником дает возможность делить прямой угол на 3 равных части, а затем получать углы, равные 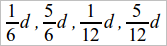
Источник
Параллелограмм: свойства и признаки
О чем эта статья:
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
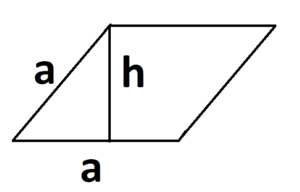
- S = a × h, где a — сторона, h — высота.
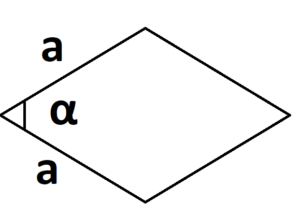
- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.
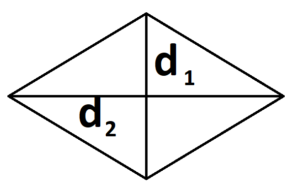
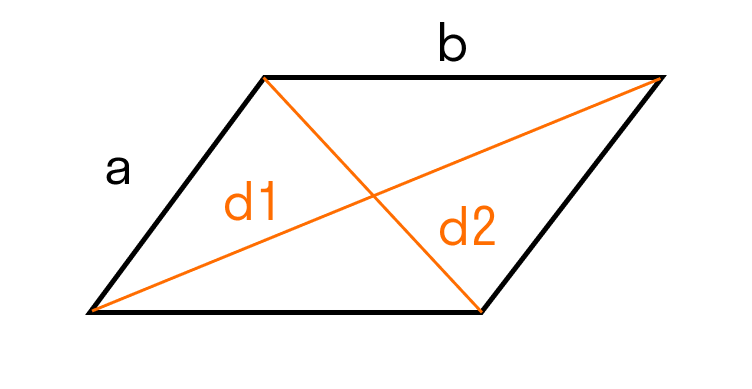
- Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные занятия по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
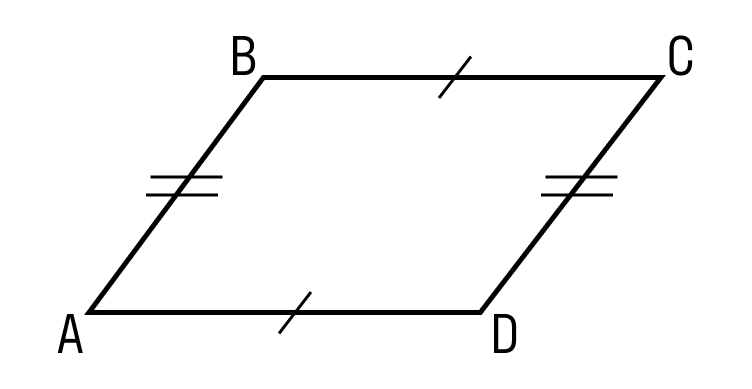
- Противоположные стороны параллелограмма равны.
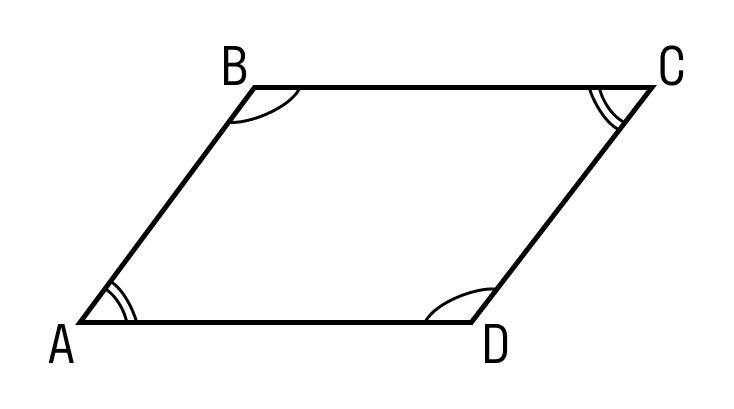
ABCD — параллелограмм, значит, AB = DC, BC = AD. - Противоположные углы параллелограмма равны.
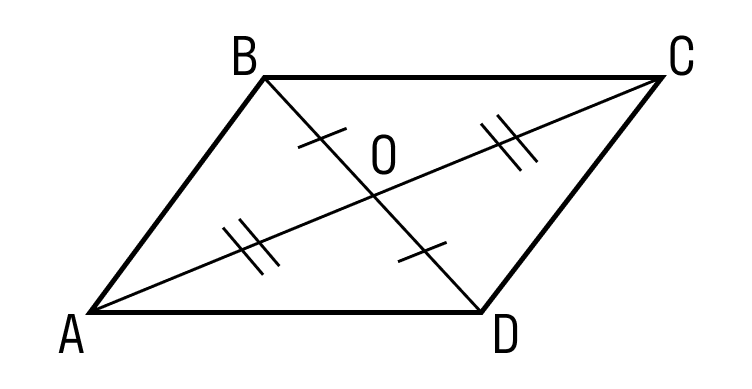
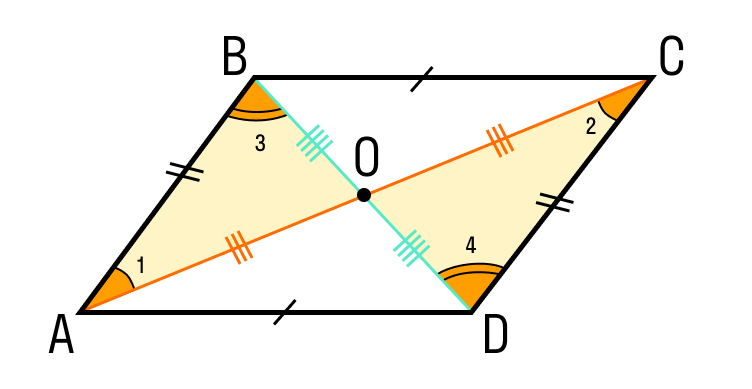
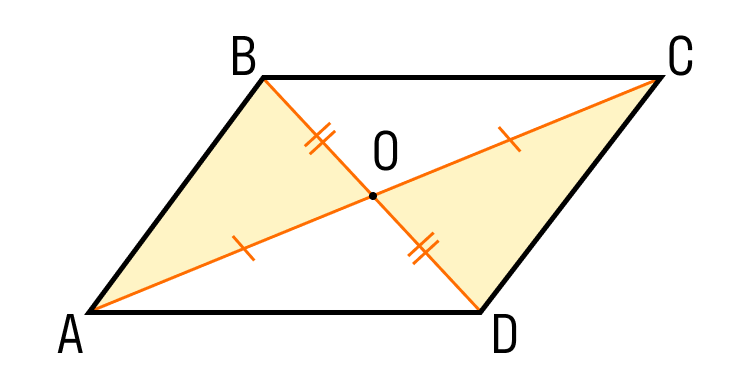
ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D. - Диагонали параллелограмма точкой пересечения делятся пополам.
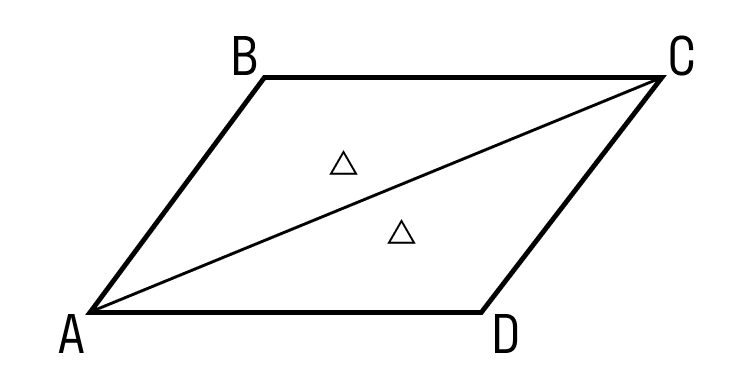
ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC. - Диагональ делит параллелограмм на два равных треугольника.
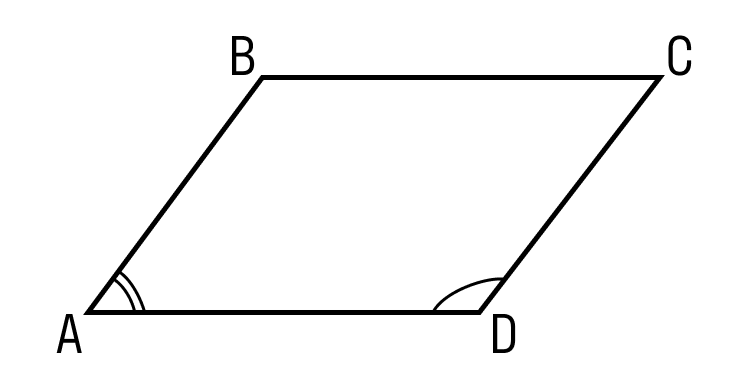
ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA. - Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
ABCD — параллелограмм, значит, ∠A + ∠D = 180°. - В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1 2 + d2 2 = 2 × (a 2 + b 2 ).
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- AB = CD как противоположные стороны параллелограмма.
- ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
- Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
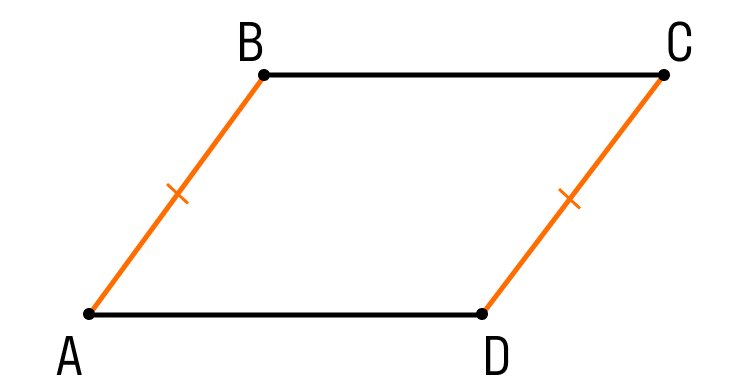
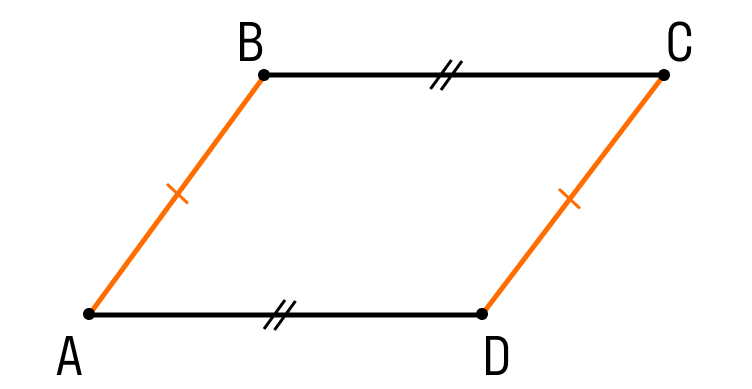
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB || CD
- AB = CD
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
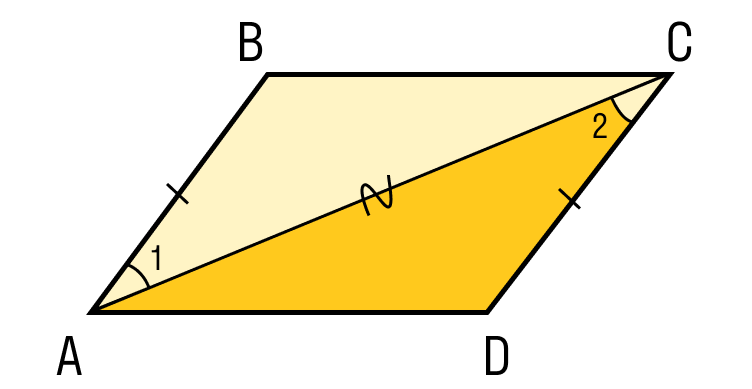
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB = CD
- BC = AD
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
- AC — общая сторона;
- AB = CD по условию;
- BC = AD по условию.
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Источник