- Отрицание высказываний и высказывательных форм
- Конспект урока математики на тему : Отрицание высказываний
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
Отрицание высказываний и высказывательных форм
Пусть предложение А – высказывание. Если перед сказуемым данного предложения поставить частицу «не» либо перед всем предложением поставить слова «неверно, что», то получится новое предложение, которое называется отрицанием данного и обозначается 
Определение. Отрицанием высказывания А называется высказывание 
Таблица истинности отрицания имеет вид:
| А | 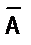 |
| и | л |
| л | и |
Из данного определения следует, что предложение и его отрицание не могут быть ни одновременно истинны, ни одновременно ложны.
Построим, например, отрицание ложного высказывания «число 28 делится на 9»:
а) Число 28 не делится на 9.
б) Неверно, что число 28 делится 9.
Высказывания, которые мы получили, истинные. Значит, отрицание данного предложения построено правильно.
Рассмотрим теперь правила построения отрицания конъюнкции и дизъюнкции высказываний. Если перед всем составным высказыванием поставить слова «неверно, что», то, безусловно, получим его отрицание. А как быть с частицей «не»? Можно ли поставить ее перед сказуемым составного предложения и получить его отрицание? Возьмем, например, высказывание «число 28 делится на 9 и на 4». Оно ложное, так как представляет собой конъюнкцию двух высказываний, одно из которых ложно. Поставив перед сказуемым этого высказывания частицу «не», получим конъюнкцию «число 28 не делится на 9 и на 4», в которой одно из предложений «число 28 не делится на 4» – ложное и, значит, ложно построенное с помощью частицы «не» предложение. Поэтому оно не является отрицанием высказывания «число 28 делится на 9 и на 4».
Можно доказать, что отрицание конъюнкции двух высказываний А и В является дизъюнкцией их отрицаний. Для этого надо убедится в том, что значения истинности высказываний вида 


| А | В | А Ù B |  |  | 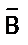 | 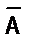 Ú Ú 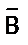 |
| И | и | и | л | л | л | л |
| И | л | л | и | л | и | и |
| Л | и | л | и | и | л | и |
| Л | л | л | и | и | и | и |
Про высказывания вида 





Аналогично можно доказать, что имеет место равносильность 


Эти равносильности носят название законов де Моргана.
Из них вытекает следующее правило построения отрицания конъюнкции и дизъюнкции: чтобы построить отрицание конъюнкции (дизъюнкции), достаточно заменить отрицаниями составляющие ее высказывания, а союз «и» («или») заменить союзом «или» («и»).
Задача 1. Построить отрицание высказывания «число 28 делится на 9 или на 6».
Решение (два способа).
1) Поставим перед данным высказыванием слова «неверно, что». Получим высказывание «неверно, что число 28 делится на 6 или на 6», которое является отрицанием исходного.
2) Воспользуемся законом де Моргана: заменим высказывания «число 28 делится на 9» и «число 28 делится на 6» их отрицаниями, а союз «или» поменяем на союз «и». Получим высказывание «число 28 не делится на 9 и не делится на 6», которое также является отрицанием исходного.
Итак, мы выяснили, как строить отрицание конъюнкции и дизъюнкции высказываний. А как быть с высказываниями, которые содержат кванторы? Достаточно ли для отрицания таких предложений поставить перед сказуемым частицу «не»? Например, будет ли отрицанием высказывания «всякий прямоугольный треугольник является равнобедренным» предложение «всякий прямоугольный треугольник не является равнобедренным»? Видим, что не будет, так как оба высказывания ложны. Таким образом, строить отрицания высказываний с квантором при помощи частицы «не» перед сказуемым нельзя.
Остается другой путь – перед всем предложением, ставим слова «неверно, что». Тогда отрицанием высказывания «всякий прямоугольный треугольник является равнобедренным» будет предложение «неверно, что всякий прямоугольный треугольник является равнобедренным», но это предложение имеет тот же смысл, что и предложение «некоторые прямоугольные треугольники не являются равнобедренными».
Отрицанием высказывания «некоторые прямоугольные треугольники являются равнобедренными» является высказывание «неверно, что некоторые прямоугольные треугольники являются равнобедренными».
Вообще если дано предложение («х) А(х), то его отрицанием будут предложения 
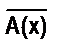
Получаем две равносильности: 



Из них вытекает правило: для того чтобы построить отрицание высказывания, начинающегося с квантора общности (существования), достаточно заменить его квантором существования (общности) и построить отрицание предложения, стоящего после квантора.
Задача 2. Построить отрицание высказывания «некоторые однозначные числа делятся на 10».
Решение. Сделать это можно двумя способами.
1) Поставим перед высказыванием слова «неверно, что». Получим высказывание «неверно, что некоторые однозначные числа делятся на 10», которое является отрицанием данного.
2) Заменим квантор существования (он выражен словом «некоторые») на квантор общности «все» и построим отрицание предложения, стоящего после слова «некоторые», поставив частицу «не» перед сказуемым. Получим высказывание «все однозначные числа не делятся на 10».
Последнее, о чем пойдет речь, — это отрицание высказывательных форм.
Пусть на множестве Х задана высказывательная форма А(х). Ее отрицание обозначим 





Доказательство этого равенства мы опускаем.
Пусть, например, на множестве натуральных чисел задана высказывательная форма А(х) – «число х кратно 5». Тогда ее отрицанием будет предложение «число х не кратно 5» (или «неверно, что число х кратно 5»), истинное при всех значениях х, которые не кратны 5.
Источник
Конспект урока математики на тему : Отрицание высказываний
Министерство образования и науки РД
ГБПОУ «Профессионально- педагогический колледж имени Р. Гамзатова».
Разработка урока по математике
Тема: Отрицание высказываний.
2015-2016 уч. год.
Тема: Отрицание высказываний.
Цели : Ознакомить с правилами построения отрицаний высказываний ; совершенствовать навыки по определению значений истинности различных математических предложений; развивать навыки логического мышления и интерес к математике.
Оборудование : таблицы, тесты.
Повторение пройденного материала.
Объяснение нового материала.
Закрепление нового материала.
Итоги урока. Домашнее задание.
-Здравствуйте, сегодня мы закрепим знания о конъюнкции и дизъюнкции высказываний, о высказываниях с кванторами и научимся строить отрицания различных видов высказываний.
Повторение пройденного материала.
— Сначала выполним несколько заданий на повторение пройденного материала.
Что называется высказыванием? Что называется высказывательной формой?
а) Среди предложений укажите высказывания и высказывательные формы
В сутках 48 часов.
Почему снег белый?
Число х кратно 2.
Что больше: 5 или 7?
б) Придумайте предложение являющееся высказыванием.
Приведите пример предложений, не являющихся высказываниями.
в) Среди предложений укажите истинное высказывание.
Волга впадает в Черное море.
г) Придумайте два истинных и два ложных высказывания.
д) Верно ли высказывание? Объясните.
Через две точки можно провести несколько прямых.
Уравнение x+7=5 не имеет корней.
Число 4 является корнем уравнения 72:х=18.
Что называется конъюнкцией высказываний? Что называется дизъюнкцией высказываний?
Определите значение истинности высказываний.
Число 16 кратно 2 и нечетное.
Число 20 делится на 3 или на 6.
Квадрат является прямоугольником или трапецией.
Решите систему неравенств и уравнение и покажите связь с конъюнкцией и дизъюнкцией высказывательных форм
4) — Какие различают кванторы?
— Как показать истинность и ложность высказываний с квантором общности?
— Как показать истинность и ложность высказываний с квантором существования?
Существует число, которое делится на 7.
Все четырехугольники – квадраты.
Любое двузначное число больше 5.
Среди прямоугольных треугольников есть равносторонние.
Поставьте вместо многоточия логическую связку «и» или «или», чтобы получилось истинное высказывание
а) Число 18 четное … кратно 9.
б) Прямоугольник является трапецией … параллелограммом.
в) Число 10 делится на 5 … однозначное.
г) Число 12 кратно 2 … 6.
2) Вместо многоточия поставьте квантор, чтобы получилось истинное высказывание
а) … число кратно 5.
б) … прямоугольник является параллелограммом.
в) … натуральное число больше 0.
г) … треугольник является равносторонним.
3) Решите систему неравенств и уравнение и покажите связь с конъюнкцией и дизъюнкцией высказывательных форм, если хϵ R
Поставьте вместо многоточия логическую связку «и» или «или», чтобы получилось истинное высказывание
а) Число 21 меньше 8 … нечетное.
б) Квадрат является ромбом … прямоугольником.
в) Число 18 делится на 3 … больше 5.
г) Трапеция является четырехугольником … квадратом.
2) Вместо многоточия поставьте квантор, чтобы получилось истинное высказывание
а) … равносторонний треугольник является равнобедренным.
б) … число четное.
в) … двузначное число больше 9.
г) … трапеция является равнобокой.
3) Решите систему неравенств и уравнение и покажите связь с конъюнкцией и
дизъюнкцией высказывательных форм, если хϵ R
Объяснение нового материала.
Часто в математике приходится строить отрицания высказыванийй.
Пусть А-высказывание. Если перед сказуемым данного предложения поставить частицу «не», либо перед всем предложением поставить слова «неверно, что», то получится предложение, которое называется отрицанием данного высказывания и обозначается А (читается: «не А» или «неверно, что А»).
Определение: Отрицанием высказывания А называется высказывание А, которое ложно, когда высказывание А истинно, и истинно, когда высказывание А-ложно.
Пример: А: Число 16 делится на 9.
А: а) Число 16 не делится на 9.
б) Неверно, что число 16 делится на 9.
Рассмотрим теперь правила построения отрицания конъюнкции и дизъюнкции высказываний.
Чтобы построить отрицание конъюнкции и дизъюнкции, достаточно заменить отрицаниями составляющие ее высказывания, а союз «и» («или») заменить союзом «или» («и»).
Это правило можно записать в виде равносильностей А˄В ⇔ А˅В и А˅В ⇔ А˄В.
Эти равносильности называют законами де Моргана.
1) Построить отрицание высказывания: «Число 25 кратно 3 или 5».
Отрицание можно построить двумя способами:
а) Неверно, что число 25 кратно 3 или 5.
б) Число 25 не кратно 3 или 5.
2) Построить отрицание высказывания: «Число 6 четное и делится на 4».
Отрицание можно построить двумя способами.
а) Неверно, что число 6 четное и делится на 4.
б) Число 6 нечетное или не делится на 4.
Теперь рассмотрим правила построения отрицаний высказываний, которые содержат кванторы.
Для того, чтобы построить отрицание высказывания, начинающегося с квантора общности (существования), достаточно заменить его квантором существования (общности) и построить отрицание предложения, стоящего после квантора.
Это правило можно записать двумя раносильностями:
( ∀ х) А(х) ⇔ ( ∃ х) А(х) и ( ∃ х) А(х) ⇔ ( ∀ х) А(х)
1) Построить отрицание высказывания: «Некоторые студенты отличники».
Отрицание можно построить двумя способами:
а) Неверно, что некоторые студенты отличники.
б) Всякий студент не отличник.
2) Построить отрицание высказывания: «Все числа больше 10»
Отрицание можно построить двумя способами:
а) Неверно, что все числа больше 10
б) Существуют числа не больше 10
Закрепление нового материала.
Сформулируйте отрицания следующих предложений двумя способами:
Квадрат является ромбом.
а) Неверно, что квадрат является ромбом.
б) Квадрат не является ромбом.
Число 6 однозначное и меньше 8.
а) Неверно, что число 6 однозначное и меньше 8.
б) Число 6 не однозначное или не меньше 8.
Трапеция является параллелограммом или прямоугольником.
а) Неверно, что трапеция является параллелограммом или прямоугольником.
б) Трапеция не является параллелограммом и прямоугольником.
Всякое число четное.
а) Неверно, что всякое число четное.
б) Существует число, которое не является четным.
Хотя бы одно число четное.
а) Неверно, что хотя бы одно число четное.
б) Любое число нечетное.
Итоги урока. Домашнее задание.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 821 человек из 76 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 290 человек из 69 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 605 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-538382
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Российские школьники завоевали пять медалей на олимпиаде по физике
Время чтения: 1 минута
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года
Время чтения: 1 минута
Спортивные и творческие кружки должны появиться в каждой школе до 2024 года
Время чтения: 1 минута
Минпросвещения будет стремиться к унификации школьных учебников в России
Время чтения: 1 минута
Правительство предложило потратить до 1 млрд рублей на установку флагов РФ у школ
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник









