Как пользоваться способом перемены плоскостей

58. Способ замены плоскостей проекций

Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым углом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи. Для решения одних задач достаточно заменить одну плоскость, но если это решение не обеспечивает требуемого расположения геометрической фигуры, можно провести замену двух плоскостей.

Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.

Рассмотрим решение четырех исходных задач способом замены плоскостей проекций.

1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня.

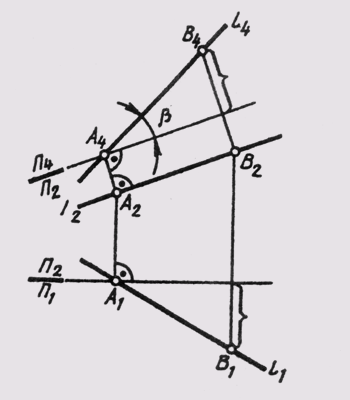
Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций П₄, расположив ее параллельно самой прямой и перпендикулярно одной из основных плоскостей проекций, т. е. от системы плоскостей П₁_|_П₂ перейти к системе П₄ _|_ П₁ или П₄ _|_ П₂. На чертеже новая ось проекций должна быть параллельна одной из основных проекций прямой. На рис. 108 построено изображение прямой l (А, В) общего положения в системе плоскостей П₁ _|_ П₄, причем П₄ || l. Новые линии связи A₁A₄ и В₁В₄проведены

перпендикулярно новой оси —П₁/П₄ параллельной горизонтальной проекции l₁.

Новая проекция прямой дает истинную величину А₄В₄отрезка АВ (см. § 11) и позволяет определить наклон прямой к горизонтальной плоскости проекций (а = L₁П₁). Угол наклона прямой к фронтальной плоскости проекций (b = L₁П₂) можно определить, построив изображение прямой на другой дополнительной плоскости П4_|_П₂ (рис. 109).

2. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций она заняла проецирующее положение.

Чтобы на новой плоскости проекций изображение прямой было точкой (см. § 10), новую плоскость проекций нужно расположить перпендикулярно данной прямой уровня. Горизонталь будет иметь своей проекцией точку на плоскости П₄_|_ П₁. (рис. 110), а фронталь f— на П₄_|_ П₂

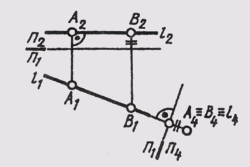
Если требуется построить вырожденную в точку проекцию прямой общего положения, то для преобразования чертежа потребуется произвести две последовательные замены плоскостей проекций. На рис. 111 исходный чертеж прямой l (А,В) преобразован следующим образом: сначала построено изображение прямой на плоскости П₄_|_ П₂, расположенной параллельно самой прямой l. В системе плоскостей П₂_|_ П₄, прямая заняла положение линии l уровня (А₂А₄ _|_П₂/П₁;

П₄ _|_П₅, причем вторая новая плоскость проекций П₅ перпендикулярна самой прямой l. Так как точки А и В прямой находятся на одинаковом расстоянии от плоскости П₄, то на плоскости П₅ получаем изображение прямой в виде точки (А₅ = B₅ = l₅).

3. Преобразовать чертеж плоскости общего положения так, чтобы относительно новой плоскости она заняла проецирующее положение.

Для решения этой задачи новую плоскость проекций нужно расположить перпендикулярно данной плоскости общего положения и перпендикулярно одной из основных плоскостей проекций. Это возможно сделать, если учесть, что направление ортогонального проецирования на новую плоскость проекций должно совпадать с направлением соответствующих линий уровня данной плоскости общего положения. Тогда все линии этого уровня на новой плоскости проекций изобразятся точками, которые и дадут «вырожденную» в прямую проекцию плоскости (см. § 47).

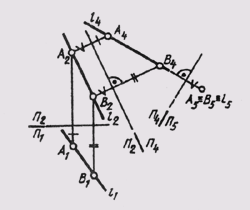
На рис. 112 дано построение нового изображения плоскости 0 (ABC) в системе плоскостей П₄ _|_П₁. Для этого в плоскости 0 построена горизонталь h(A, 1), и новая плоскость проекций П₄ расположена перпендикулярно горизонтали h. Графическое решение третьей исходной задачи приводят к построению изображения плоскости в виде прямой линии, угол наклона которой к новой оси проекции П₁/П₄, определяет угол наклона а плоскости Q(ABC) к горизонтальной плоскости проекций (а = Q ^ П₁).

Построив изображение плоскости общего положения в системе П₂ _|_П₄, (П₄ расположить перпендикулярно фронтали плоскости),

можно определить угол наклона Р этой плоскости к фронтальной плоскости проекций.

4. Преобразовать чертеж проецирующей плоскости так, чтобы относительно новой плоскости она заняла положение плоскости уровня.

Решение этой задачи позволяет определить величину плоских фигур.

Новую плоскость проекций нужно расположить параллельно заданной плоскости. Если исходное положение плоскости было фронтально проецирующим, то новое изображение строят в системе и П₂ _|_П₄, а если горизонтально проецирующим, то в системе П₁ _|_П₄. Новая ось проекций будет расположена параллельно вырожденной проекции проецирующей плоскости (см. § 47). На рис. 113 построена новая проекция А₄В₄С₄горизонтально проецирующей плоскости Sum (ABC) на плоскости П₄ _|_П₁

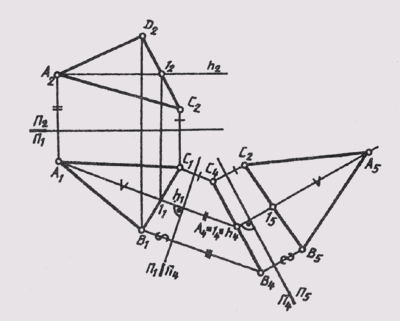
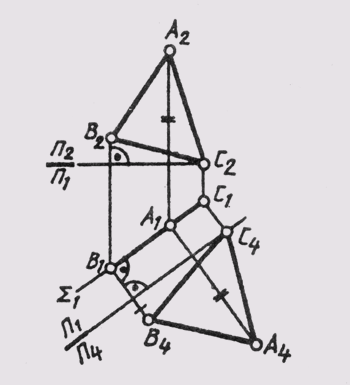
Если в исходном положении плоскость занимает общее положение, а нужно получить изображение ее как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно задачу 3; а затем задачу 4. При первой замене плоскость становится проецирующей, а при второй — плоскостью уровня (рис. 114).

В плоскости А(DEF) проведена горизонталь h (D — 1). По отношению к горизонтали проведена первая ось П₁ / П₄ _|_h₁. Вторая новая ось

проекций параллельна вырожденной проекции плоскости, а новые линии связи — перпендикулярны вырожденной проекции плоскости. Расстояния для построения проекций точек на плоскости П₅ нужно замерить на плоскости П₁от оси П₁ / П₂и откладывать по новым линиям связи от новой оси П₄ /П₅. Проекция D₅E₅F₅треугольника DEF конгруэнтна самому треугольнику ABC.

С применением способа замены плоскостей можно решать ряд других задач как самостоятельных, так и отдельных частей задач, включающих большой объем графических решений.

Источник

Способ перемены плоскостей проекций

Этот способ широко применяют в машиностроении и приборостроении. Сущность способа перемены плоскостей проекций заключается в следующем: положение точек, линий, плоских фигур, поверхностей в пространстве не изменяется, а система V, Н дополняется плоскостями, образующими с V, или Н, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.

Каждая новая система выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла положение, наиболее удобное для выполнения требуемого построения.

На рисунке 5.1 показано преобразование проекций точки А из системы V, Н в систему S, Н, в которой вместо плоскости V введена новая плоскость S, а плоскость Н осталась неизменной. При этом S перпендикулярна Н. В системе S, Н горизонтальная проекция а точки А осталась неизменной. Проекция a_s точки А на плоскости S находится от плоскости Н на том же расстоянии, что и проекция a’ точки А на плоскости V. Это условие позволяет легко строить проекцию точки на чертеже (рис. 5.2) на новой плоскости проекций. Для этого в новой системе (Н, S) из проекции точки (а) на сохраняющейся плоскости проекций проводят линию связи, перпендикулярную к новой оси проекций (S/H). На этой линии связи отмечают расстояние от оси до проекции a_s точки на новой плоскости проекций S, равное расстоянию от преобразуемой проекции точки а ‘ до оси проекций V/H в системе V, Н (| аs—2| = | а’—1| ).

При введении новой плоскости проекций, перпендикулярной фронтальной плоскости проекций (например, плоскости Т на рис. 5.3), расстояние от проекции (bt) до новой оси проекций равно расстоянию от горизонтальной проекции (b) до оси V/H (|b-1| = |b_t-2|).

В дальнейшем, при введении новой плоскости проекций, ось проекций можно обозначать в виде дроби, черта которой лежит на оси; каждую букву при этом пишут как бы на «своей» плоскости.

Проекции точек на новых плоскостях проекций удобно отмечать индексами плоскости (например, а, bt, и т. п.).

Перемену плоскостей проекций можно производить последовательно несколько раз.

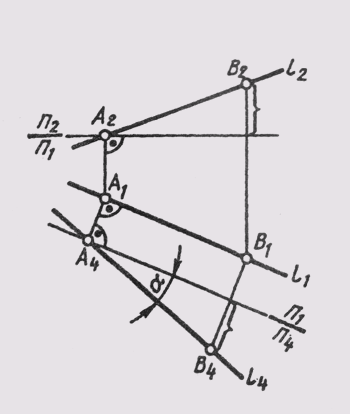
Четыре основные задачи преобразования. Определение величины отрезка АВ общего положения показано на рисунке 5.4. Для этого плоскость V заменена на новую плоскость проекций S, параллельную отрезку (ось S/H параллельна оси ab). Расстояния от оси S/H до at и bt соответственно равны расстояниям от а’ и b’ до оси V/H соответственно (|аt—2|—|а’—1|). Одновременно с определением натуральной величины отрезка определена величина а угла наклона отрезка АВ к плоскости Н.

Приведение отрезка прямой общего положения в проецирующее положение. На рисунке 5.4 новая система плоскостей проекций H/S относительно отрезка АВ находится в частном положении (пл. S || АВ). Введем еще одну новую плоскость проекций Т, перпендикулярную плоскости проекций S и отрезку АВ (ось проекций T/S перпендикулярна проекции a_sь_s). Относительно этой плоскости проекций Т отрезок АВ занимает проецирующее положение (проекции аt и bt совпадают, | а—2| = | аt—3| ).

Для преобразования проекций отрезка общего положения на чертеже в проецирующее положение требуется введение двух новых плоскостей проекций последовательно: первой — параллельно отрезку, второй — перпендикулярно ему с условием перпендикулярности между исходными и новыми плоскостями проекций.

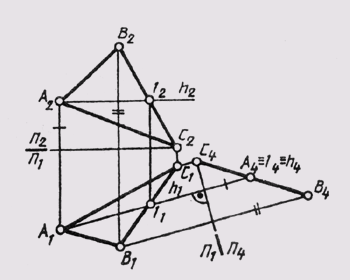
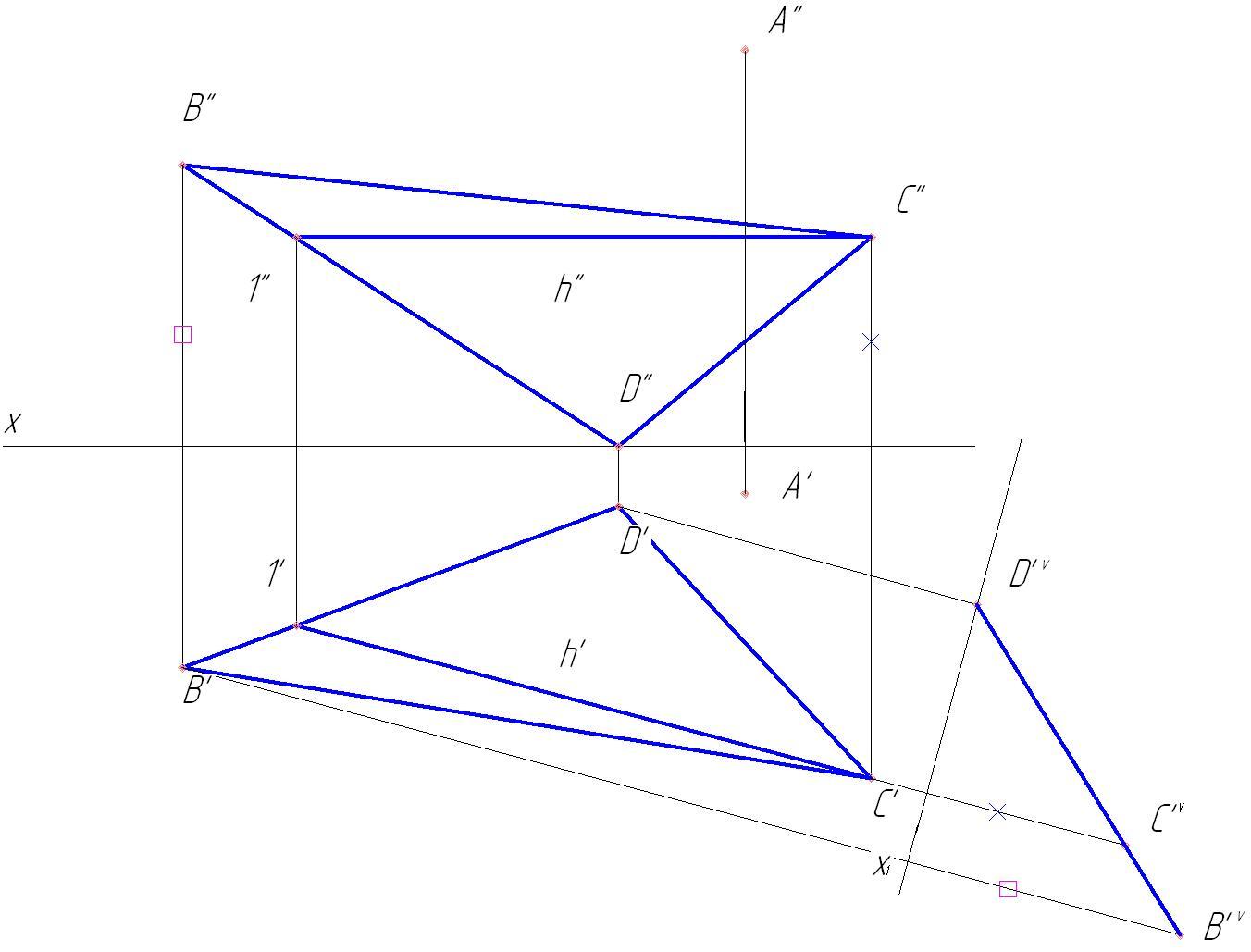
Приведение плоской фигуры общего положения в проецирующее положение. Решение основывается на предыдущей задаче. Построение выполняют с помощью одной из линий частного положения, например горизонтали с проекциями a’f’, af (рис. 5.5). Новая плоскость проекций S в этом случае выбрана перпендикулярно горизонтали AF (ось перпендикулярна проекции af) и соответственно перпендикулярно плоскости Н.

Определение натурального вида плоской фигуры, расположенной в проецирующем положении (рис. 5.6). Построение выполнено путем введения новой плоскости проекций Т, перпендикулярной плоскости V и параллельной плоскости четырехугольника с проекциями a’b’c’d’ и а, b, с, d (ось T/V параллельна проекции a’b’c’d’). Проекция atbtctdt является натуральным видом заданного четырехугольника.

Следовательно, последовательным введением двух новых плоскостей проекций могут быть определены: натуральный вид плоской фигуры, принадлежащей плоскости общего положения, и углы наклона плоскости к плоскостям проекций.

Определение расстояния между двумя скрещивающимися прямыми. Это расстояние выражается величиной общего перпендикуляра MN к заданным прямым АВ и CD (рис. 5.7, а). Для определения его длины удобно, чтобы одна из прямых располагалась перпендикулярно плоскости проекций. Выше было показано, что для этого надо последовательно ввести две новые плоскости проекций (рис. 5.7, б), например:

На плоскость Т прямая АВ проецируется в точку a_t=b_t. Проведя перпендикуляр из точки аt=bt, на проекцию ctdt находим проекцию п, точки N пересечения его с прямой CD. Отметим

проекцию т, точки М, совпадающую с проекциями точек аtbt. Искомое расстояние определено — m_tn_t. На чертеже стрелками указано построение проекций тп и т’п ‘ общего перпендикуляра к двум скрещивающимся прямым в системе V, Н.

Источник

Способ перемены плоскостей проекций

Сущность способа состоит в том, что положение в пространстве объекта проецирования не изменяется, а одну из плоскостей проекций заменяют на новую, располагают ее перпендикулярно ко второй плоскости проекций, но в более выгодной позиции для решения задачи (рис.92).

На рис.93 изображены проекции точки А в системе π₁ ∕π₂ . Для замены плоскости π₂ на π₂₁вводим новую ось Х₁ и изображаем точку в системе π₁ ∕π_21. Положение оси Х₁ в данном примере выбрано произвольно, так как не решается конкретная задача. Расстояние новой проекции точки от новой оси равно расстоянию заменяемой проекции от заменяемой оси. В нашем примере A»₁A_x1=A»A_x=z_A. Линии проекционной связи всегда перпендикулярны осям.

Рис.93

Заменой одной плоскости пользуются при определении истинной величины отрезка прямой общего положения и углов наклона ее к плоскостям проекций при преобразовании плоскости общего положения в проецирующую.

На рис.94 показано определение истинной величины отрезка АВ и угла наклона его к плоскости π₁. Отрезок АВ преобразуем во фронталь. Новую ось Х₁ проводим параллельно горизонтальной проекции отрезка А’B’. Новая фронтальная проекция A IV B IV ₁ и есть истинная величина отрезка. Угол α — угол наклона отрезка АВ к плоскости π₁.

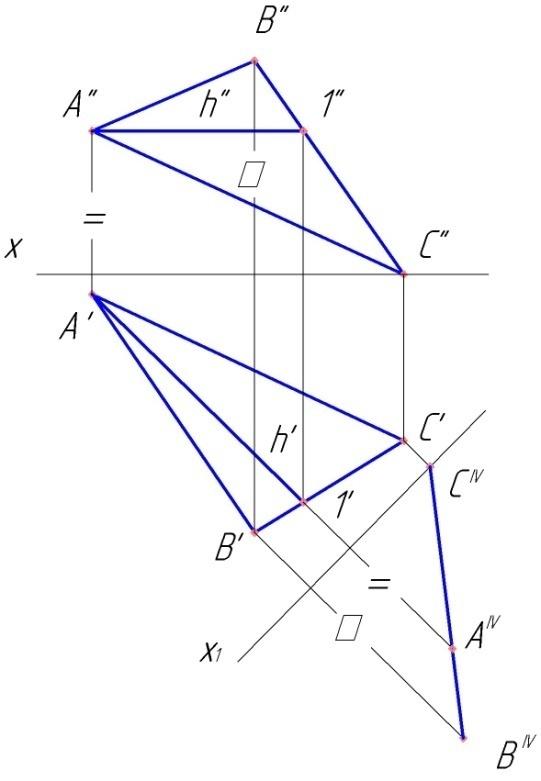
При решении задач на определение истинной величины плоской фигуры нужно применять две вспомогательные плоскости, разберем это на определении истинной величины треугольника ABC общего положения (рис.95).

Первая замена: в треугольнике ABC проводим горизонталь h и делаем ее проецирующей. Ось x_1┴h’. На новую плоскость π4 треугольник проецируется в виде отрезка прямой C IV A IV B IV . При первой замене плоскости мы преобразовали плоскость треугольника во фронтально-проецирующую.

Вторая замена: новую ось Х₂ проводим || собирательному фронтальному следу C IV A IV B IV . Строим новую горизонтальную проекцию ΔАВС — в системе плоскостей π₄∕ π₅

Истинная величина фигуры по площади всегда больше любой из ее проекций. В этом методе всегда нужно обозначать оси проекций и положение самих плоскостей.

В этом методе всегда нужно обозначать оси проекций и положение самих плоскостей.

Рис.96

Метрические задачи с применением методов преобразования проекций

Эти задачи можно классифицировать на определение расстояний, определение углов, определение истинных величин плоских фигур. Часть задач мы уже рассмотрели при изучении методов преобразования.

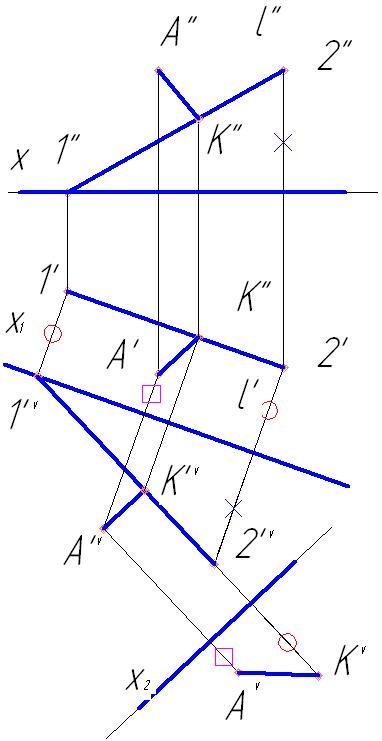
Пример 1. Определить расстояния от точки А до прямой l (рис.97).

Рис.97

Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.

1. На эпюре проекции перпендикуляра к прямой можно построить, если прямая параллельна плоскости проекций. Поэтому сначала строим дополнительную ортогональную проекцию прямой и точки А на плоскости π₄, параллельной прямой _l и перпендикулярной к π₁. При этом ось Х₁ параллельна _l′.

Для построения дополнительной проекции прямой _l на ней отмечены точки 1 и 2 (рис.98).

2. Проводим дополнительную проекцию А IV K IV перпендикуляра (А IV K IV _l IV ), а затем строим горизонтальную проекцию А′К′. Построена также и фронтальная А′′К′′ проекция перпендикуляра АК.

По двум данным проекциям отрезка АК (А′К′ и А IV K IV ) находим его длину, построив дополнительную ортогональную проекцию отрезка на плоскости π₅, параллельной АК и перпендикулярной к π₄ (рис. 99).

Аналогично можно определить расстояние между двумя параллельными прямыми.

Пример 2. Определить расстояние от точки А до плоскости α(ΔВСD) (рис.100).

Рис.100

Расстоянием от точки до плоскости является длина отрезка перпендикуляра, опущенного из точки на плоскость.

Если плоскость является проецирующей, то перпендикуляр к ней параллелен плоскости проекций, и длина проекции его отрезка на этой плоскости проекций равна искомому расстоянию. Исходя из этого построим дополнительную ортогональную проекцию плоскости α и точки А на плоскости π4, перпендикулярной к плоскости α и к плоскости π1.

1. Плоскость π₄ будет перпендикулярна к плоскости α, если она перпендикулярна к горизонтали этой плоскости. При этом ось х₁ перпендикулярна к горизонтальной проекции h′ горизонтали h плоскости α. Дополнительной ортогональной проекцией плоскости α на плоскость π₄ является прямая B IV C IV D IV (рис.101).

Рис.101

Из точки А IV опускаем перпендикуляр А IV K IV на прямую B IV C IV D IV . Длина отрезка А IV K IV равна расстоянию от точки А до плоскости α(ΔBCD) (рис.102). Построим проекции отрезка АК. Горизонтальная проекция А′К′ параллельна оси х₁, так как отрезок АК параллелен плоскости π₄, и перпендикулярна к горизонтальной проекции h′ горизонтали h плоскости α. Фронтальную проекцию К′′ точки К строим по двум ее проекциям К′ и K IV .

На основании решения рассмотренной задачи можно определить расстояние между параллельными прямой и плоскостью, между двумя параллельными плоскостями.

Рис.102

Пример3. Найти расстояние между параллельными плоскостями.

Решение задачи на определение расстояния между двумя плоскостями сводится к построению перпендикуляра, опущенного из любой точки одной плоскости на другую.

Рис.103

Преобразуем плоскости общего положения α и γ в плоскости проецирующие. В нашем примере во фронтально-проецирующие. Новую ось X₁ проводим _┴горизонтальным следам h_0α и h_0γ. Для построения новых фронтальных следов используем произвольную точку M на одном из фронтальных следов. На плоскости π4 опускаем перпендикуляр. Это и будет истинная величина расстояния между плоскостями α и γ. Строим горизонтальную и фронтальную проекцию перпендикуляра, зная, что горизонтальная проекция перпендикуляра M’N ’перпендикулярна горизонтальному следу плоскости, а фронтальная M”N”- фронтальному следу плоскости.

Источник