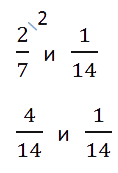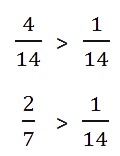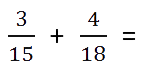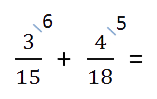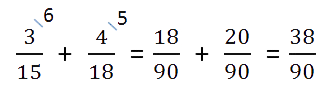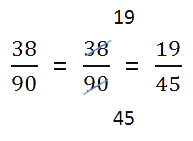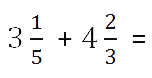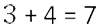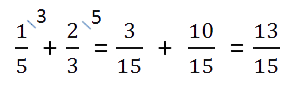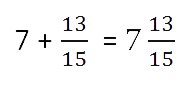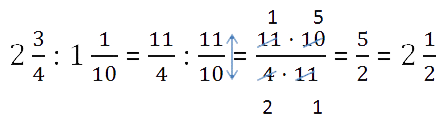Как получают дроби 2 способа

Обыкновенные дроби. Получение дробей

Разделы: Математика

Математика в коррекционной школе VIII вида является одним из основных учебных предметов.

Цель: добиться овладения учащимися системой доступных математических знаний, умений и навыков, необходимых в повседневной жизни и в будущей профессии, так прочно, чтобы они стали достоянием учащихся на всю жизнь.

Задачи преподавания математики по вспомогательной школе состоят в том, чтобы:

• дать учащимся такие доступные количественные, пространственные и временные геометрические представления, которые помогут им в дальнейшем включиться в трудовую деятельность;
• использовать процесс обучения математике для повышения уровня общего развития учащихся вспомогательных школ и коррекции недостатков их познавательной деятельности и личностных качеств;
• воспитывать у учащихся целенаправленность терпеливость, работоспособность, настойчивость, трудолюбие, самостоятельность, навыки контроля и самоконтроля, развивать точность и глазомер, умение планировать работу и доводить начатое дело до завершения.

Обучение математике во вспомогательной школе носит предметно-практическую направленность, тесно связано с жизнью и профессионально-трудовой подготовкой учащихся, другими учебными предметами. Раздел «Обыкновенные дроби» является как раз таки жизненно-практическим.

Доли.

Первое представление о доле, которая получается путем деления целого предмета на равные части, учащиеся получают в 5-м классе школы VIII вида.

1. На каждую парту выдается одно яблоко. Проблема как разделить его на двоих? Ребята предлагают разрезать яблоко пополам. И дальше идет разговор о том, «разрезать пополам – это значит разделить на две равные части». В результате такого деления получаются две половины, или две вторые доли.
2. Каждый ребенок получает прямоугольник, но для того, чтобы дети убедились, что при делении целого на две равные части его вторые доли равны, а половины, полученные от деления разных целых не равны, прямоугольники делаем разного размера. Согнуть прямоугольник пополам, сравнить полученные доли, затем сравнить наложением эти доли с тем, что получилось у соседа по парте.
3. Аналогичное задание можно дать, раздав детям круги разных размеров, равнобедренные треугольники, квадраты.
4. На следующем этапе все эти фигуры дети сами рисуют, вырезают, сгибают пополам, очень хорошо полученные доли наклеить в тетрадь.
5. Интересно поработать с квадратом и прямоугольником, предложить детям разделить их на две части разными способами.

Отработав деление на две части таким же образом можно делить прямоугольники, круги, квадраты, отрезки на четыре части. Деление на три, пять, семь, восемь и т.д. частей удобно объяснять на полосках длиной 3см, 5см, 7см, 8см и т.д. Отрезки, полоски, чертим в тетради, раскрашиваем. Большое внимание необходимо уделить построению окружности. Детям интересен циркуль, и они с большим удовольствием с ним работают.

Дроби.

После того как усвоено понятие «доля», переходим к понятию «дробь».

До недавнего времени ребята при делении чисел не раз убеждались в том, что не все числа делятся нацело, может получиться остаток, деление же меньшего числа на большее невозможно. В то же время в повседневной жизни им приходилось делить две булочки на три равные части и т.д. опираясь на жизненный опыт учащихся, нужно показать, что при делении целого числа на целое получается дробь. При этом деление возможно даже тогда, когда делимое меньше делителя.

К доске приглашаются три человека. Им дается два яблока. Проблема как разделить на троих два яблока? Ребята предлагают разрезать каждое яблоко на три части. Каждый ребенок получит по третьей доле от каждого яблока. На доске и в тетради делаем запись 2:3=.
А затем можно выполнять задания следующего содержания.

Начертите в тетради прямоугольник длиной 3 сантиметра и шириной 1 сантиметр. Разделите его на три равные части, одну часть закрасьте.

Начертите в тетради прямоугольник длиной 5 сантиметров и шириной 1 сантиметр. Разделите его на пять равных частей, две части закрасьте.

Начертите в тетради прямоугольник длиной 7 сантиметров и шириной 1 сантиметр. Разделите его на семь равных частей, четыре части закрасьте.

Начертите в тетради прямоугольник длиной 4 сантиметра и шириной 1 сантиметр. Разделите его на четыре равные части, три части закрасьте.

Чтобы получить дробь, мы целое делим на равное количество частей (долей) и берем одну или несколько частей (долей).

Дробные числа записывают с помощью натуральных чисел и черты. Например, одну четвертую долю записывают так:

Такие записи, и называют обыкновенными дробями. В дроби число, стоящее над чертой, называют числителем дроби, а число, стоящее под чертой, называют знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей разделена единица, а числитель дроби показывает, сколько таких частей взято. Целесообразно в тетради сделать следующую запись:

Читают дроби так: сначала называют числитель, потом знаменатель.

Например: — одна третья, — две пятых, — четыре седьмых, — три четвертых.

При чтении дробей надо помнить: числитель дроби — количественное числительное женского рода (одна, две, четыре и т.д.), а знаменатель — порядковое числительное (третья, пятая, седьмая, четвертая и т.д.).

Для закрепления навыков записи и чтения обыкновенных дробей проводится математический диктант:

Записать дроби: . Прочитать полученные дроби.

Математические диктанты одна из интересных форм работы, я часто ею пользуюсь при изучении тем «Правильные и неправильные дроби», «Основное свойство дроби», «Преобразование обыкновенных дробей».

1. Записать дроби: . Подчеркнуть правильные дроби. Обвести в кружок дроби с одинаковым знаменателем.
2. Возможен такой вариант диктанта: записать дроби в два столбика, в первый – правильные, во второй — неправильные: .
3. Записать дроби: . Выписать из них сократимые, и выполнить сокращение.
4. Записать дроби: . Выписать из них неправильные и превратить в смешанные.

Все эти задания можно оформить в виде карточек.

Источник

Прочитайте дроби 3/8, 2/21, 7/80. Объясните как можно получить каждую из этих дробей (два способа)

Ответ или решение 2

Читаем дроби

• 3/8 — числитель: три; знаменатель: восьмых; читаем дробь: три восьмых;
• 2/21 — числитель: два; знаменатель: двадцать первых; читаем дробь: две двадцать первых;
• 7/80 — числитель: семь; знаменатель: восьмидесятых; читаем дробь: семь восьмидесятых.

Как получить каждую из этих дробей

Первый способ: Чтобы получить дробь 3/8, необходимо отрезок разделить на 8 частей и взять 3 части.

Второй способ: Из дроби 6/16, сократив числитель и знаменатель на 2. Получаем 6 : 2/16 : 2 = 3/8. Или из дроби 9/24, сократив числитель и знаменатель на 3. Получаем: 9 : 3/24 : 3 = 3/8.

Первый способ: Чтобы получить дробь 2/21, необходимо отрезок разделить на 21 часть и взять 2 части.

Второй способ: Из дроби 4/42, сократив числитель и знаменатель на 2. Получаем: 4 : 2/42 : 2 = 2/21. Или из дроби 6/63, сократив числитель и знаменатель на 3. Получаем: 6 : 3/63 : 3 = 2/21.

Первый способ: Чтобы получить дробь 7/80, необходимо отрезок разделить на 80 частей и взять 7 частей.

Второй способ: Из дроби 14/160, сократив числитель и знаменатель на 2. Получаем: 14 : 2/160 : 2 = 7/80. Или из дроби 21/240, сократив числитель и знаменатель на 3. Получаем: 21 : 3/240 : 3 = 7/80.

Источник

Обыкновенные дроби

О чем эта статья:

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

• Половина — одна вторая доля предмета или 1/2.
• Треть — одна третья доля предмета или 1/3.
• Четверть — одна четвертая доля предмета или 1/4.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Виды дробей:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 — 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Основные свойства Дробь не имеет значения, при условии, если делитель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

1. В обеих дробях знаменатель равен 5.
2. В первой дроби числитель равен 1, во второй дроби равен 4.

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

1. Приведем дроби к общему знаменателю:
   
2. Сравним дроби с одинаковыми знаменателями:
   

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к наименьшему общему знаменателю (НОЗ);
• сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

1. Найти наименьшее общее кратное (НОК) знаменателей дробей, которое станет их общим знаменателем.
2. Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
3. Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Найдем наименьшее общее кратное для определения единого делителя.

Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

Полученные числа запишем справа сверху над числителем.

Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.

Проверим полученный результат:

• если делимое больше делителя, нужно преобразовать в смешанное число;
• если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

1. Сложить целые части.
   
   
2. Сложить дробные части.
   

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Суммировать полученные результаты.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

1. преобразовать смешанные дроби в неправильные;
2. перемножить числители и знаменатели дробей;
3. сократить полученную дробь;
4. если получилась неправильная дробь, преобразовать в смешанную.

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

• числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
• знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

• представить числа в виде неправильных дробей;
• разделить то, что получилось друг на друга.

Источник