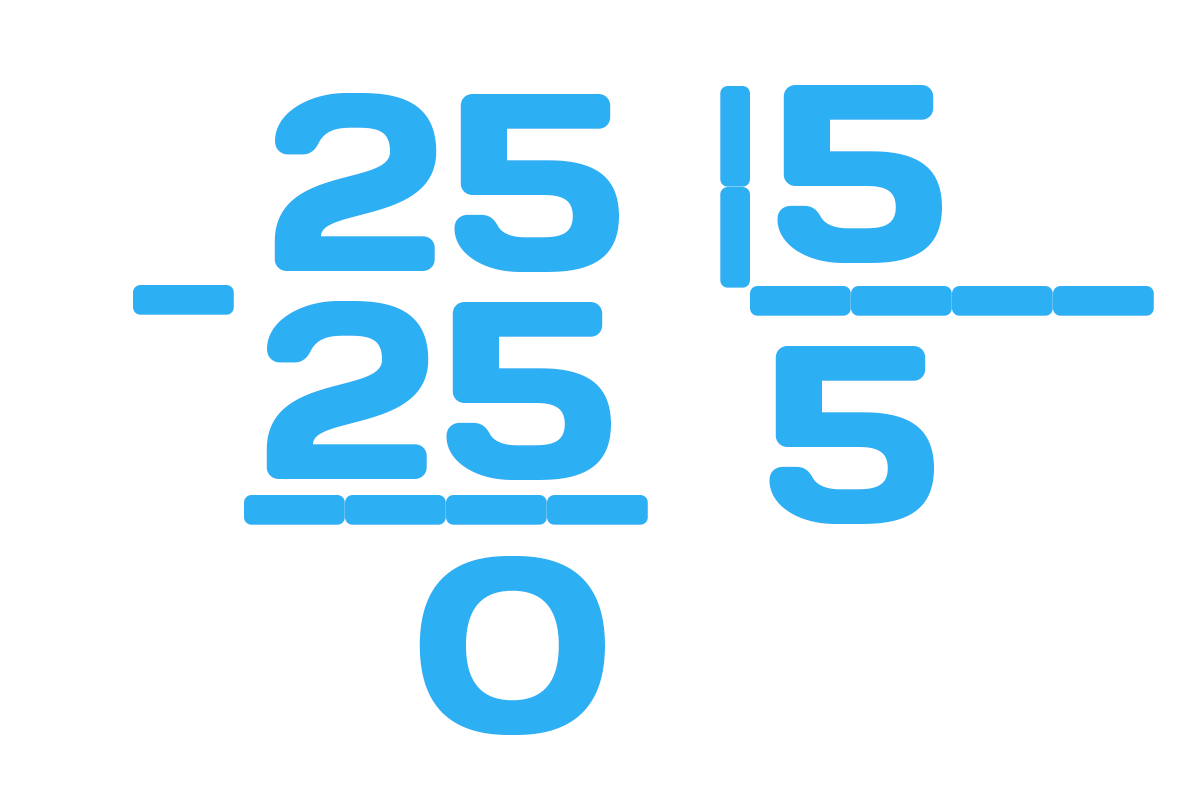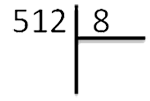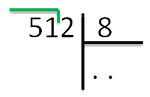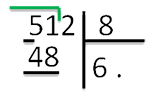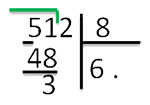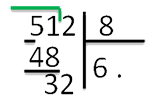Как поделить удобным способом

Деление

Деление – одна из четырех основных математических операций (сложение, вычитание, умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение. 3*3=9. Верно? Абсолютно.

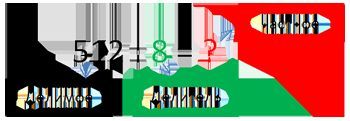
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение. В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

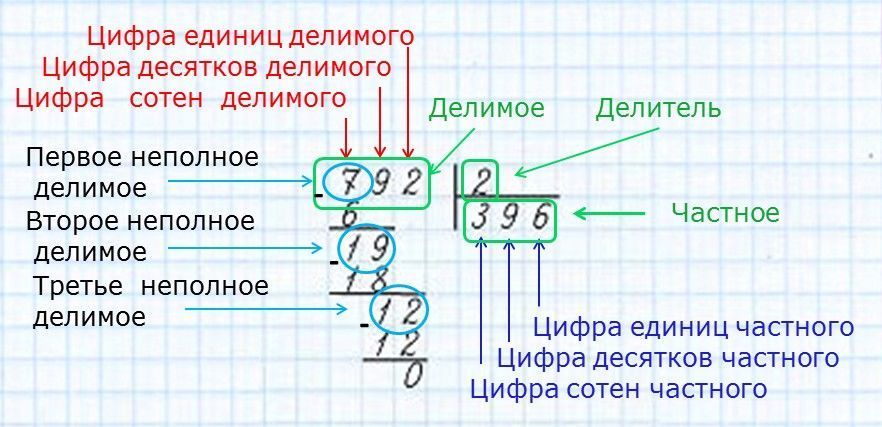
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

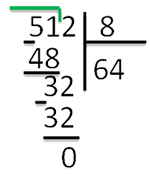
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг. Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг. Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг. Ставим точку под делителем.

5 шаг. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг*. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Источник

Как доступно объяснить ребёнку суть деления чисел

Освоение арифметических действий порой даётся детям нелегко. Но если родители дошкольников, непонимающих умножение, деление, относительно спокойны: ещё есть пару лет до школы, а там — будет видно, то мамы и папы младших школьников иногда приходят в исступление от бессилия растолковать своему чаду, что значит деление чисел. На самом деле, ничего сложного для ребёнка и методически непостижимого для взрослого в этом нет.

Как объяснить деление дошкольнику

Малыши-дошколята вовлекаются в процесс деления с самого раннего возраста, например, когда угощают конфетами друзей, делятся игрушками в песочнице. Поэтому задача родителей заключается в том, чтобы обобщить этот детский опыт для освоения азов арифметики, дать понимание принципа деления, то есть разделения предметов на равные доли. При этом базовыми знаниями, необходимыми для освоения деления в дошкольном возрасте, является понимание, что такое целое, больше/меньше. Если с этими понятиями ребёнок знаком, то можно вооружаться играми и на их основе поэтапно объяснять деление.

Делим поровну

Для начала нужно показать малышу на доступном для его понимания уровне, что такое деление, используя наглядность. В этом поможет игра «Тебе и мне поровну».

Материалы для тренировки арифметических действий должны быть вкусными

1. Малыш получает 6 конфет.
2. Взрослый просит поделить конфеты на двоих так, чтобы у каждого было одинаковое количество.
3. Ребёнок раскладывает конфеты по одной, пересчитывая их в обеих кучках.
4. После того, как конфеты поделены, юный математик ещё раз пересчитывает их в каждой кучке, а затем считает, сколько сладостей всего.
5. Количество «делителей» можно увеличивать, но «делимое» всегда должно делиться без остатка. Так у ребёнка формируется представление о том, что такое поровну.

Деление с остатком

Освоив деление без остатка, можно переходить к следующему этапу — игре «Всем поровну и «хвостик».

Оставшееся яблоко можно отдать взрослому или игрушке, а потому сравнить, у кого больше/меньше

1. Ребёнок получает 4 яблока.
2. Взрослый просит разделить их поровну между тремя членами семьи.
3. Оставшееся яблоко является остатком, который получается тогда, когда поровну поделить нельзя.

Разобравшись с делением поровну и с остатком, можно переходить к освоению абстрактного деления, то есть вычислениям с использованием цифр, а не конфет-яблок-игрушек. Для этого нужно сказать, что первое число — это то, что мы делим: конфеты, игрушки, яблоки, а второе — участники этого деления, то есть члены семьи, друзья. Но главное здесь, сколько предметов в итоге будет у участников.

Видео: как освоить деление за 5–10 минут

Что нужно для освоения деления в младшем школьном возрасте

Деление — это не первое арифметическое действие, которое осваивают дети. Поэтому, прежде чем браться за «делимое-делитель-частное», нужно обязательно выяснить, знает ли ребёнок разряды чисел и понимает ли принципы:

По аналогии с таблицей умножения, существует таблица деления, которую также можно заучить. Однако методисты склоняются к тому, что гораздо важнее понимание ребёнком механизмов выпонения арифметического действия, чем механическое заучивание.

Таблицей деления дети могут проверять решения примеров

Эффективные способы объяснения деления школьникам

Все способы объяснения можно условно поделить на академичные и образные. Первые опираются на цифры, то есть записываются в виде арифметических примеров, вторые — на конкретные предметы: конфеты, мячи и т. д., которые умозрительно делятся между людьми, игрушками.

В работе с учениками начальной школы эффективным будет синтетический способ, совмещающий опору на образы и цифры одновременно.

Деление на основе знания таблицы умножения

Для понимания сути деления стоит обратиться к вычислениям с опорой на таблицу умножения.

1. Записываем пример: 2 х 5 = 10.
2. Берём 10 монет и просим поделить их на двоих — получается две стопки по 5 монет.
3. Далее 10 монет делим на пятерых — получается 5 стопок по 2 монеты.
4. Вывод — при делении мы выясняем, сколько раз каждый множитель помещается в произведении.

На этом приёме разъясняем понятийную базу: то число, которое делится, называется делимое, то число, на которое делится — делителем, а результат — частным.

Поскольку деление обратно умножению, то второе может проверить результат первого.

Первое время для закрепления навыка можно зарисовывать схему перестановки значений при делении и при проверки умножением

1. Делимое делим на делитель, то есть 10 : 2.
2. Получаем частное — 5.
3. Проверяем умножением, то есть частное умножаем на делитель — 5 х 2.
4. Получаем 10, что в исходном примере является делимым.

Деление двузначных чисел на однозначные

Чтобы разделить двузначное число, не являющееся произведением таблицы умножения, на однозначное, нужно каждую цифру делимого разделить на делитель и записать первое частное десятками, а второе — единицами. Например, 86 : 2.

1. Делим 8 на 2. Получаем 4.
2. Делим 6 на 2. Получаем 3.
3. Ответ — 43.
4. Проверяем — 43 х 2 = 86.

Деление способом группирования

Суть этого способа деления заключается в подсчёте количества групп равных делителю, которые помещаются в делимое. Результат будет частным.

Задача состоит в распределении мячей между командами. Решаем пример — 30 : 3.

Группирование предполагает использование наглядных материалов

Как объяснить деление в столбик

Поскольку деление может быть без остатка, а может быть с остатком, рассмотрим два варианта объяснение такого арифметического действия.

Деление без остатка

Решим пример 396 : 3.

Выполняя деление в столбик, ребёнок должен правильно оформить запись, чтобы значения «не съехали» с нужных позиций

Деление с остатком

Решим пример 90 : 4.

Важно обратить внимание ребёнка на то, что перед добавлением нуля к остатку в столбике, нужно поставить десятичную запятую в частном

Видео: как научиться делить в столбик

Деление на двузначные числа

Если в делителе есть десятки, сотни, то для облегчения решения делитель можно упростить, разбив на единицы (десятки).

Для деления на десятки нужно воспользоваться правилом упрощения

1. Решим пример — 405 : 15.
2. Разобьём 15 на единицы, на 5 и 3 — их произведение равно 15.
3. Теперь решаем два примера. Сначала 405 : 5. Частное 81.
4. Затем 81 : 3. Частное 27.
5. Результат — 405 : 15 = 27.

Видео: тренажёр быстрого деления в уме для школьников

Объяснить деление можно не только школьнику, но и дошкольнику. Причём не только в условиях детского сада, школы, но и дома. Для этого нужно убедиться, что ребёнок имеет опорные знания, и у родителя есть запас времени, терпения для регулярных занятий со своим чадом.

Источник