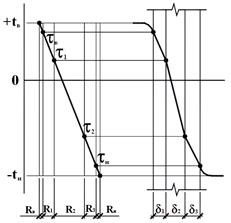
Графический метод определения температур внутри ограждения
Практика показывает, что для выполнения ряда теплотехнических расчетов важное значение имеет определение не только температуры наружной и внутренней поверхности ограждающей конструкции, то и температуры любой точки в толще ограждения. Эта задача проще решается графическим способом. На произвольно принятой горизонтальной прямой отложить последовательно в одинаковом масштабе сопротивление тепловосприятию Rв, температурное сопротивление каждого из слоев конструкции Ri, сопротивление теплопередаче Rн. Сумма составит общее сопротивление теплопередаче R0. На внутренней линии откладываем температуру внутреннего воздуха (положительную – вверх от оси), и наружного (отрицательную – вниз). Полученные точки соединим прямой линией. Рядом вычертить в масштабе схему ограждающей конструкции и перенести температуры, соответствующие границам слоев.
Распределение температур в слоистом ограждении имеет характер ломанной линии (рисунок 12).
Рисунок 12 – Распределение температур в слоистом ограждении
Тема 4 Обеспечение защитных свойств ограждения
Передача тепла через ограждения в нестандартных условиях
Колебания температуры наружного воздуха вызывают колебания внутренней температуры. Изменения температуры постоянно действуют на ограждения. Вследствие периодических колебаний внутренней и наружной температуры необходимы дополнительные требования к ограждению: обеспечение минимального колебания температуры на внутренней поверхности ограждения в целях обеспечения комфортных условий в помещении, а также во избежание образования конденсата на поверхности конструкции.
Свойство ограждающей конструкции сохранять относительное постоянство температуры на внутренней поверхности при периодических колебаниях температуры наружной поверхности называется теплоустойчивостью ограждения.
На теплоустойчивость ограждения влияет теплоусвоение его поверхности, т.е. свойство этой поверхности воспринимать тепло при периодических колебаниях теплового потока или температуры воздуха, которое характеризуется коэффициентом теплоусвоения материала S, м 2 °С/Вт.
Коэффициент теплоусвоения S материала – это отношение амплитуды колебаний потока тепла к амплитуде колебаний температуры на поверхности ограждения.
Значение коэффициента теплоусвоения S внутренней поверхности ограждения из однородного материала значительной толщины зависит от коэффициента теплопроводности l, удельной теплоемкости с, плотности материала g, а так же от периода колебания теплового потока z.
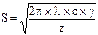
В таблице 9 приведены коэффициенты теплоусвоения некоторых материалов.
Коэффициенты теплоусвоения
| Материалы | ||||
| Сталь | Гранит | Минеральная вата | Пенопласт | |
| S, Вт/(м 2 °С) | 125,7 | 24,9 | 0,64 | 0,26 |
С изменением температуры на поверхности ограждения связаны ее колебания внутри ограждения. Амплитуда колебаний температуры в толще ограждения отстает во времени от колебаний на поверхности и затухает по мере удаления от нее. Каждому моменту времени соответствует своя волнообразная кривая распределения температуры в слоях ограждения, смещенная по отношению к предыдущей кривой.
При этом в ограждении есть слой резких колебаний температур dt, где происходит изменение температуры примерно в 2 раза.
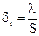
Например. Слои резких колебаний для кирпича:
для периода 24 часа – 0,084 м;
для периода 12 часов – 0,06 м.
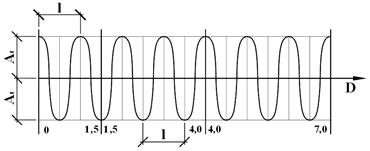
Расстояние между двумя максимумами или минимумами волны называется длиной волны.
Количество температурных волн l, размещающихся в толще ограждения, пропорционально показателю тепловой инерции D, который служит критерием оценки степени затухания температурных колебаний и называется условной толщиной ограждения (рисунок 13).
Рисунок 13 – К определению показателя тепловой инерции D
Свойство ограждения сохранять или медленно изменять распределение температуры внутри конструкции называется тепловой инерцией.
Чем больше инерция, тем труднее изменить первоначальное состояние ограждения. Например, кирпичные массивные стены долго сохраняют свою «летнюю» температуру и не чувствительны к резким и кратковременным перепадам температур наружного воздуха в осенний период. Чтобы получить нормальные условия после отключения системы отопления в весенний период, промерзшие кирпичные стены надо очень долго прогревать. Поэтому летом в кирпичных домах бывает прохладно.
Наружные стены с тепловой инерцией менее 4 в районах со среднемесячной температурой июля 21°С и выше в летний период года подвергаются не только колебаниям температуры наружного воздуха в течение суток, но и активно нагреваются солнечными лучами в дневное время. Поэтому требуется расчет теплоустойчивости ограждающих конструкций [2]. Допустимая (требуемая) амплитуда колебаний температуры внутренней поверхности ограждения определяется по формуле:
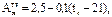
где tн – среднемесячная температура наружного воздуха за июль, °С
Амплитуда колебаний температуры внутренней поверхности ограждения определяется по формуле:
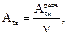
где Аtв расч. – расчетная амплитуда колебаний температуры наружного воздуха, °С, n – величина затухания расчетной амплитуды колебаний температуры наружного воздуха с учетом солнечной радиации:
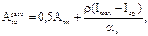
где Аtn – максимальная амплитуда суточных колебаний температуры наружного воздуха в июле, °С [1]; r – коэффициент поглощения солнечной радиации материалом наружной поверхности ограждающей конструкции; Imax и Iср. – максимальное и среднее суточное значение суммарной солнечной радиации (прямой и рассеянной), Вт/м 2 , падающей на вертикальные поверхности западной ориентации (при расчете стен) и на горизонтальные поверхности (для покрытий); aн – коэффициент теплоотдачи наружной поверхности ограждения по летним условиям, Вт/(м 2 °С):

где u – минимальная из средних скоростей ветра за июль, повторяемость.
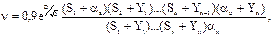
где е = 2,718 – основание натурального логарифма; Д – тепловая инерция ограждения; S1…Sn – расчетные коэффициенты теплоусвоения материала слоев ограждения [2, приложение 3*]; Y1…Yn – коэффициенты теплоусвоения наружной поверхности отдельных слоев ограждения, Вт/(м 2 °С).
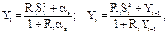
где aв – коэффициент теплоотдачи внутренней поверхности ограждения.
Показатель тепловой инерции: для однородного ограждения
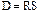
для многослойных ограждений
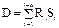
Источник
Графический и табличный методы анализа тепловых процессов в задачах по физике.
Графический и табличный методы анализа тепловых процессов в задачах по физике.
Описаны методы и приёмы, используемые автором в своей практической деятельности, при изучении тепловых явлений в 8-м и 10-м классах. Примеры и иллюстрации, приведённые в данном материале, позволяют продемонстрировать образцы решения задач по термодинамике.
В педагогической деятельности учителя физики приходится достаточно часто сталкиваться с трудностями понимания учащимися анализа тепловых процессов. В результате, казалось бы, простые задачи оказываются нерешенными. А ведь с уравнением теплового баланса в курсе физики школьники встречаются дважды: в 8-м и в 10-м классах, причём сложность изучения данной темы в старших классах возрастает в разы. Но если в основной школе ученик не понял чего-то, то в 10-м классе всё приходится начинать сначала.
При поиске решения данных проблем нужно учитывать два важных параметра:
Методы решения должны быть наглядными и универсальными;
Доступными для понимания и применения большинству учащихся непрофильных классов.
Анализ учебно-методической литературы и контрольно-измерительных материалов показал, что графическое представление тепловых процессов позволяет значительно упростить поиск решения и составление уравнений, а также выявить скрытые процессы, т.е. обнаружить подводные камни. В статье представлено обобщение опыта работы автора по теме «Тепловые явления»
Уравнение теплового баланса. Изменение агрегатных состояний вещества
Многие обучающиеся испытывают сложности при составлении уравнений для решения задач, в которых происходит теплообмен между несколькими телами с учётом изменения агрегатного состояния этих тел. Можно использовать схемы, отображать процессы с помощью кругов, но, как выяснилось, все эти способы выраженного положительного эффекта не дают.
Перед тем как перейти к непосредственному рассмотрению приёмов решения задач по теме «Тепловые явления», нужно отметить три важных замечания по методике изложения и изучения данной темы:
Необходимо изначально показать обучающимся важность составления и записи уравнения теплового баланса в общем виде:
Научить различать процессы, сопровождающиеся выделением и поглощением теплоты, и подставлять в уравнение с учётом отданного и полученного количества теплоты.
Научить читать графики изменения температуры агрегатного состояния вещества.
Методика решения подобных задач с учётом перехода из одного агрегатного состояния в другое у каждого учителя своя, но любому учителю физики всегда важно рассмотреть и альтернативную точку зрения. Плюсы и минусы своих вариантов всегда становятся более заметными в сравнении с предложениями коллег.
Предлагаю рассмотреть метод, состоящих всего из двух этапов:
Графическая интерпретация условия задачи.
Составление уравнения теплового баланса для данной задачи, используя график, после чего начинается непосредственное математическое решение задачи.
В качестве примера рассмотрим несколько задач, начиная с самой простой с постепенным усложнением. Обязательным условием в задачах будет наличие двух и более тел.
Задача №1 (без изменения агрегатных состояний веществ):
В латунный калориметр массой 128 г, содержащий 240 г воды при температуре 8,4 0 С, опущено металлическое тело массой 192 г, нагретое до 100 0 С. Окончательная температура, установившаяся в калориметре, 21,5 0 С. Определите удельную теплоёмкость испытуемого тела [1].
Решение:
Графически показываем изменение температуры всех тел, указанных в задаче. Видно, что в уравнении теплового баланса будет три слагаемых. Для удобства можно записать уравнения для каждого участка в отдельности:
Составляем уравнение согласно графику:
И вот теперь начинается самое важное – математическое решение задачи.
На первых же занятиях нужно обозначить целесообразность решения задачи в общем виде. Показать на примерах, что решение по действиям веет к округлениям, и как следствие – неправильному ответу. Ведь подстановка данных в выраженную из формулы величину позволяет быстро и безошибочно получить верный результат.
Задача №2 (с изменением агрегатных состояний веществ):
Смесь, состоящую из 5 кг льда и 15 кг воды при общей температуре 0 0 С, нужно нагреть до температуры 80 0 С пропусканием водяного пара при температуре 100 0 С. Определить необходимое количество пара [1].
Графически показываем изменение температуры всех тел, указанных в задаче. Видно, что в уравнении теплового баланса будет пять слагаемых. Для удобства можно записать уравнения для каждого участка:
Составляем уравнение согласно графику:
Задача №3 (с изменением агрегатного состояния части одного из веществ):
В бак, содержащий воду массой 10 кг при температуре 20 0 С, бросили кусок железа массой 2 кг, нагретый до температуры 500 0 С. При этом некоторое количество воды превратилось в пар. Конечная температура, установившаяся в баке, равна 24 0 С. Определить массу воды, обратившейся в пар [1].
Графически показываем изменение температуры всех тел, указанных в задаче. Видно, что в уравнении теплового баланса будет четыре слагаемых. Для удобства можно записать уравнения для каждого участка:
Составляем уравнение согласно графику:
Данный метод позволяет наглядно увидеть, что происходит в задаче с веществами и какие уравнения необходимы для решения задачи.
Первый закон термодинамики для изопроцессов и КПД тепловой машины.
Данная тема при своей простоте, вызывает серьёзные затруднения у выпускников при решении задач 28 и 30 части 2 ЕГЭ по физике.
Так же, как и в предыдущем случае, предлагаемый метод предполагает выполнение следующих задач:
Научить обучающихся анализировать графики тепловых процессов для начала с помощью таблицы (для начала).
Быстро определять в различных осях координат ( p , V , T ) максимальные и минимальные значения температуры, давления и объёма газа.
Использовать уравнение Клапейрона-Менделеева для выражения внутренней энергии или работы газа через другие величины.
Научить определять работу газа на участке как площадь фигуры под ним в координатах p ( V ) .
Все эти навыки отрабатываются на каждом уроке в течение всего процесса изучения молекулярной физики газов. Необходимый уровень навыков достигается в течение нескольких занятий, после чего данный метод решения ложится в основу обобщения изученных приёмов и при подготовке к ЕГЭ ученик уже имеет необходимые знания и навыки, что позволяет сконцентрироваться на более детальном рассмотрении задач повышенной сложности.
Метод анализа тепловых процессов с позиции термодинамики состоит из двух этапов:
Анализ замкнутого цикла и заполнение расширенной таблицы.
Составление необходимых соотношений, уравнений согласно условия задачи с опорой на анализ.
Рассмотрим по аналогии с предыдущими задачами несколько типовых задач по термодинамике, применив к ним данный метод решения.
Задача №1 (определение участков, где выделялась или поглощалась теплота):
Определите на каком участке графика газу сообщалась теплота и вычислите её значение?
Анализируем график и заполняем таблицу. Из таблицы видно, на каких участках к системе подводилась теплота, а на каких отводилась. В дальнейшем можно подвести учащихся к осознанию того, что и без таблицы можно быстро определять, что теплота подводится на тех участках где происходит увеличение температуры или объёма газа. Однако надо быть аккуратным с таким утверждением и помнить об адиабатном расширении или сжатии, т.к. в таком случае никакого теплообмена не происходит.
Из таблицы выводим уравнение для расчёта количества теплоты, поступившей от нагревателя или наоборот отдаваемой в окружающую среду:
Для решения задачи остаётся лишь воспользоваться изученным уравнениями. По поводу возможного замечания о том, что при передаче теплоты холодильнику в уравнении должен быть знак «минус», можно ответить, что он появится автоматически, если ученик будет правильно выполнять расчёт изменения внутренней энергии и работы газа. Необходимо помнить, что при вычислении любого изменения необходимо отнимать начальное значение от конечного, это же касается расчёта работы газа как площади фигуры по графику процесса в осях p ( V ) .
Задача №2 (определение изменения каких-либо макропараметров):
Как изменялась температура газа на каждом участке? Опишите процессы, происходящие с газом.
Анализируем график и заполняем таблицу. Из таблицы видно, как менялась внутренняя энергия и количество теплоты, на основании табличных данных делается описание процессов и изменение температуры.
Задача №3 (расчёт КПД тепловой машины):
Определите КПД тепловой машины.
Полезную работу газа по данному графику определить очень просто, она равна площади фигуры цикла. А вот количество теплоты, подводимой к системе определить можно двумя способами. Самый быстрый – посмотреть на каких участках было увеличение температуры и объёма. Из графика видно, что изотерма, проходящая через точку 2 выше чем изотермы, проведённые через точки 1 и 3. А изотерма в точке 1 ниже чем в точке 3. Участок 2-3 изохорный процесс, поэтому количество теплоты сообщалось только на участке 1-2. К данному выводу, можно прийти и через таблицу:
Составляя уравнение КПД необходимо записать выражения изменения внутренней энергии и работы газа через p 0 и V 0 , тогда они сократятся и останется только числовое выражение.
Данная методика позволяет анализировать более сложные задачи и находить нюансы которые могут быть упущены при беглом просмотре условия задачи. Рассмотрим пример такой задачи.
Задача №4 (расчёт КПД тепловой машины):
Определите КПД тепловой машины.
Данная задача может показаться простой для ученика, но в ней есть один важный момент. При расчёте количества теплоты сообщаемой нагревателем, необходимо рассчитать положительное изменение внутренней энергии. А на данном графике, не каждый ученик сможет увидеть, что на участке 1-2 было увеличение температуры. Большая часть учащихся увидев данный участок, воспользовавшись уравнением состояния идеального газа обнаружит, что температура в точке 2 меньше температуры в точке 1, а значит было уменьшение внутренней энергии и не станут учитывать её изменение на этом участке. На самом же деле, мы имеем дело с процессом, где температура меняется по нелинейному закону (квадратичная зависимость). Температура увеличивалась от точки 1 до точки М. После чего начиналось уменьшение внутренней энергии. Таким образом количество теплоты полученной от нагревателя будет определяться как: 


Заполняя таблицу, ученики не проводя вышеописанного анализа, столкнулись бы с вопросом, как заполнить ячейку количества теплоты на участке 1-2, это послужило бы для них сигналом, что необходим детальный анализ данного участка.
Дальнейшие действия по решению данной задачи выходят за рамки темы статьи. Заметим, что здесь необходимо использовать знания из математики о линейной функции, участком которой является отрезок 1-2. Получив функциональную зависимость давления от объёма на этом участке, необходимо подставить её в уравнение Клапейрона-Менделеева и задача будет решена.
Приведенные выше методы решения задач на тепловые являения, при должном усердии и кропотливой работе учителя над формированием необходимых умений у обучающихся позволяют подготовить учеников к решению более сложных задач по тепловой физике и нивелировать их страх перед сдачей выпускного экзамена по физике. Но главным является то, что использование этих приёмов приводит к развитию нестандартного, творческого мышления школьника, независимо от профиля его обучения.
Надеемся, что предложенные приёмы решения задач по термодинамике помогут сделать изучение тепловых процессов более простым и понятным, будут способствовать формированию исследовательских навыков при решении задач и окажут положительное воздействие на интеллектуальное развитие школьников.
Список использованной литературы
Кирик, Л.А. Физика-8. Разноуровневые самостоятельные и контрольные работы. – Харьков.: «Гимназия», 2001. – 144 с.
Источник