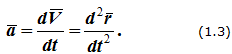Как определить траекторию при векторном способе задания движения точки

Векторный способ задания движения точки

Введение

Положение точки однозначно определяется заданием ее радиус-вектора , который изменяется со временем при движении точки. При векторном способе задания движения считается, что задан закон изменения радиус-вектора от времени . Векторный способ задания движения применяется для описания движения в общем виде, используя векторные формулы.

Например, для точки, движущейся с постоянным ускорением , радиус-вектор определяется одной векторной формулой:
,
где – постоянные векторы, не зависящие от времени. Применяя формулы, мы можем найти кинематические величины в векторном виде, не зависимо от выбранной системы координат.

При координатном способе задания движения, мы выбираем систему координат, и в ней задаем зависимости координат точки от времени . Таким образом, координатный способ привязан к выбранной системе координат, а векторный способ не зависит от системы координат.

Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.

Основные формулы при векторном способе задания движения

Скорость точки

Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.

Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.

Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.

Скорость точки направлена по касательной к траектории. Пусть – единичный вектор в направлении касательной. Тогда скорость может быть направленной либо вдоль вектора :
,
либо в противоположную сторону:
.
Чтобы охватить эти два случая, вводят алгебраическую величину скорости :
.
Это скалярная величина, равная по абсолютной величине модулю скорости, но она может принимать как положительные, так и отрицательные значения:
.
При , вектор скорости сонаправлен с . При он направлен в противоположную сторону. Величина является проекцией вектора скорости на направление . Поскольку – это единичный вектор, то
.

Единичный вектор в направлении касательной к траектории:
.

Ускорение точки

Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.

Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.

Тангенциальное ускорение

Алгебраическая величина тангенциального ускорения – это скалярная величина, равная проекции полного ускорения на направление единичного вектора , касательного к траектории:
.
Тогда вектор тангенциального ускорения можно записать в следующем виде:
.
Величина может быть как положительной, так и отрицательной. При положительном , вектор касательного ускорения сонаправлен с единичным вектором . При отрицательном – вектор касательного ускорения направлен в противоположную сторону. Модуль равен модулю касательного ускорения:
.
Алгебраическая величина тангенциального ускорения равна производной по времени от алгебраической величины скорости:
.
Производная по времени модуля скорости:
.
Если между векторами скорости и ускорения острый угол, то движение ускоренное. Если между ними тупой угол, то движение замедленное.

Нормальное ускорение

Вектор нормального ускорения:
.
; .
Единичный вектор в направлении главной нормали траектории:
.
Вектор перпендикулярен вектору и направлен к центру кривизны траектории. Нормальное ускорение всегда направлено к центу кривизны траектории. Поэтому, если выразить его через единичный вектор главной нормали:
,
то . Поэтому .
Модуль нормального ускорения равен проекции полного ускорения на направление главной нормали:
.
Имеют место следующие формулы:
.

Радиус кривизны траектории:
.
Центр кривизны траектории:
.

Единичный вектор в направлении бинормали:
.

Автор: Олег Одинцов . Опубликовано: 06-03-2016 Изменено: 29-01-2020

Источник

Векторный способ задания движения точки

Рассмотрим движение материальной точкиМ относительно некоторого тела, которое считается неподвижным. Пусть точка О – точка принадлежащая этому телу (рис.5.3). Радиус-вектор движущейся точки М относительно точкиО можно задать как вектор-функцию времени t

. (5.6)

Равенство (5.6) называется векторным уравнением движения точки или законом движения точки в векторной форме.

Кривая по которой движется точка в пространстве называется траекторией точки. Траектория – это годограф радиус-вектора точки.

Координатный способ задания движения точки

Пусть теперь вектор задан в декартовой системе координат, а— орты осейОх, Оу, Оz. Тогда вектор-функция может быть задана тремя скалярными функциями:

=++.

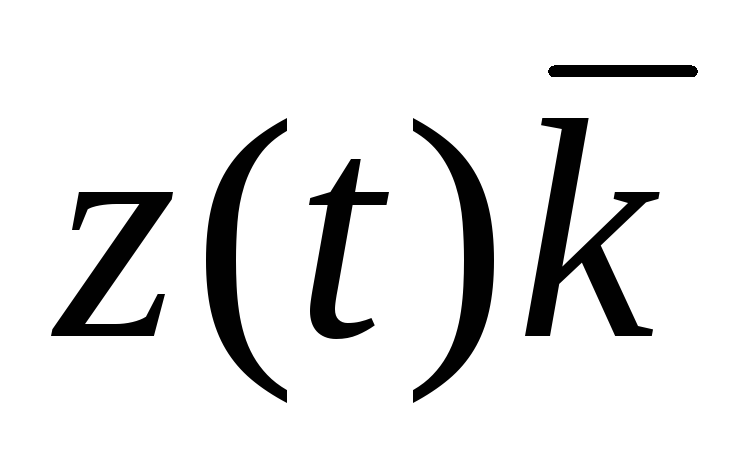
Таким образом, для того, чтобы движение точки было задано координатным способом, должны быть заданы функции:

Равенства (5.7) называются уравнениями движения точки или законом движения точки в координатной форме.

Естественный способ задания движения точки

Этот способ применяется в случае, когда траектория точки известна заранее. Траектория точки может быть задана различными способами: словесно (например, можно сказать, что траекторией точки является окружность такого-то радиуса), графически в каком-либо масштабе или уравнениями, например, в общем виде как линия пересечения поверхностей

,

или другими уравнениями.

Для задания закона движения точки по траектории необходимо выбрать на траектории точку М₀, принимаемую за начало отсчета дуговой координаты и задать положительное направление отсчета (рис. 5.4.).

При движении точки М расстояние от нее до начальной точки изменяется с течением времени, следовательно, дуговую координату необходимо задать как функцию времени:

Зависимость (5.8) называется законом движения точки. Следовательно, для того, чтобы движение точки было задано естественным способом, должны быть заданы:

положительное направление отсчета дуги s.

При этом нужно отличать дугу s и пройденный точкой путь. Если точка движется по траектории все время в одном направлении, то дуга и путь совпадают, но если, например закон движения точки равен и точка совершает гармонические колебания по кривой, то дуга и путь совпадают только до достижения дуги своего максимального значенияа. Далее путь в отличие от дуги будет все время увеличиваться.

Скорость и ускорение точки Скорость точки

Пусть движение точки задано векторным способом . На рис.5.9М и М₁  положения движущейся точки в моменты времени t и t + t.

Вектор называется вектором перемещения точки за времяt. Отношение вектора к промежут ку времени t называется средней скоростью точки за промежуток времени t

.

Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени за который произошло это перемещение, при стремлении последнего к нулю, т.е.

. (5.9)

Таким образом,скорость точки в данный момент времени равна производной радиусавектора точки по времени

. (5.10)

Это векторная величина, характеризующая быстроту изменения радиусавектора точки и направленная по касательной к траектории в сторону движения точки. Единицей измерения скорости в системе СИ является м/с.

Источник

Векторный способ задания движения точки

Средней скоростью называется физическая величина равная отношению изменения координаты точки к интервалу времени, в течение которого это изменение произошло.

Геометрический смысл средней скорости — коэффициент наклона секущей AB графика закона движения.

Для более детального, более точного описания движения, можно задать два значения средней скорости – за первую половину времени движения υ_ср1, за вторую половину — υ_ср2 .Если и такая точность нас не устраивает — то необходимо дробить временные интервалы дальше — на четыре, восемь и т.д. частей. При этом необходимо задавать соответственно четыре, восемь и т.д. значений средних скоростей. Согласитесь, такое описание становится громоздким и неудобным. Выход из этой ситуации давно найден — он заключается в том, что бы рассматривать скорость как функцию времени.

Давайте посмотрим, как будет меняться средняя скорость при уменьшении промежутка времени, за который мы эту скорость вычисляем. На рис.6 показан график зависимости координаты материальной точки от времени. Будем вычислять среднюю скорость за интервал времени от t₀ до t₁, последовательно приближая значение t₁ к t₀. При этом семейство секущих A₀A₁,A₀A₁’, A₀A₁’’ (рис.6), будет стремиться к некоторому предельному положению прямой A₀B, которая является касательной к графику закона движения. Мы приводим два различных случая, чтобы показать, что мгновенная скорость может быть как больше, так и меньше средней скорости. Эту процедуру можно описать и алгебраически, последовательно вычисляя отношения υcp=x1−x0t1−t0 , υ′cp=x′1−x0t′1−t0 , υ′′cp=x′′1−x0t′′1−t0 . При этом оказывается, что эти величины приближаются к некоторому вполне определенному значению. Это предельное значение получило название мгновенной скорости.

Векторный способ задания движения точки

В этом случае положение точки на плоскости или в пространстве определяется вектором-функцией

r=r(t)

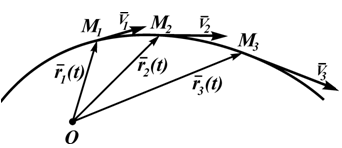
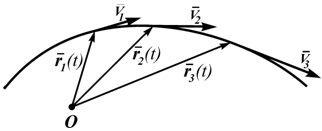
Годограф r, т.е. положение концов этого вектора в пространстве, определяет траекторию движущейся точки. Ее скорость в этом случае определяется как производная от радиуса-вектора и направлена по касательной к годографу r (по касательной к траектории движения точки, рисунок 1.1):

V=dr/dt (1.2)

Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки.

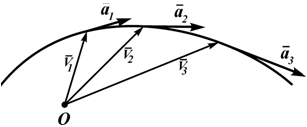
Ускорение точки (изменение ее скорости) определяется как производная от скорости:

Вектор ускорения направлен по касательной к годографу вектора скорости (рисунок 1.2, б).

Источник