Как определить способ шифрования

10 популярных кодов и шифров

Авторизуйтесь

10 популярных кодов и шифров

Коды и шифры — не одно и то же: в коде каждое слово заменяется другим, в то время как в шифре заменяются все символы сообщения.

В данной статье мы рассмотрим наиболее популярные способы шифрования, а следующим шагом будет изучение основ криптографии.

Стандартные шифры

Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, А заменяется на Б, Б — на В, и т. д. Фраза «Уйрйшоьк Рспдсбннйту» — это «Типичный Программист».

Попробуйте расшифровать сообщение:

Сумели? Напишите в комментариях, что у вас получилось.

Шифр транспонирования

В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из hello world получается dlrow olleh. Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl.

Ещё можно использовать столбчатый шифр транспонирования, в котором каждый символ написан горизонтально с заданной шириной алфавита, а шифр создаётся из символов по вертикали. Пример:

Из этого способа мы получим шифр holewdlo lr. А вот столбчатая транспозиция, реализованная программно:

Азбука Морзе

В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов:
Чаще всего это шифрование передаётся световыми или звуковыми сигналами.

Сможете расшифровать сообщение, используя картинку?

Шифр Цезаря

Это не один шифр, а целых 26, использующих один принцип. Так, ROT1 — лишь один из вариантов шифра Цезаря. Получателю нужно просто сообщить, какой шаг использовался при шифровании: если ROT2, тогда А заменяется на В, Б на Г и т. д.

А здесь использован шифр Цезаря с шагом 5:

Моноалфавитная замена

Коды и шифры также делятся на подгруппы. Например, ROT1, азбука Морзе, шифр Цезаря относятся к моноалфавитной замене: каждая буква заменяется на одну и только одну букву или символ. Такие шифры очень легко расшифровываются с помощью частотного анализа.

Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».

Однако этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов.

Шифр Виженера

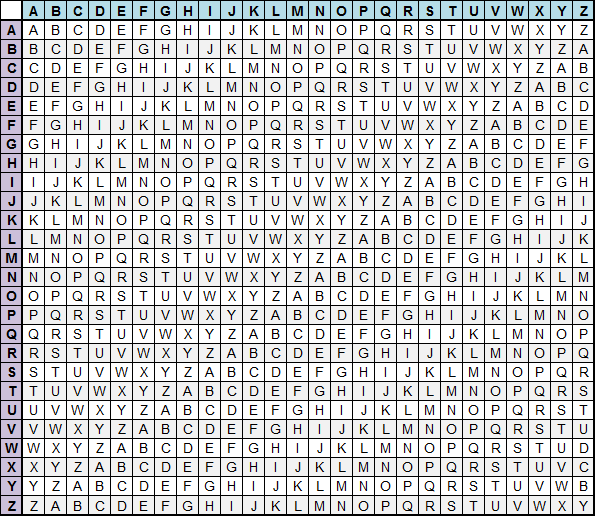
Представим, что есть таблица по типу той, что на картинке, и ключевое слово «CHAIR». Шифр Виженера использует принцип шифра Цезаря, только каждая буква меняется в соответствии с кодовым словом.

В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова «С», вторая буква — для «H», etc. Если послание длиннее кодового слова, то для (k*n+1)-ой буквы, где n — длина кодового слова, вновь будет использован алфавит для первой буквы кодового слова.

Чтобы расшифровать шифр Виженера, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания.

Попробуйте расшифровать эту фразу самостоятельно:

Подсказка длина кодового слова — 4.

Шифр Энигмы

Энигма — это машина, которая использовалась нацистами во времена Второй Мировой для шифрования сообщений.

Есть несколько колёс и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.

Существовало более ста триллионов возможных комбинаций колёс, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.

Цифровые шифры

В отличие от шифровки текста алфавитом и символами, здесь используются цифры. Рассказываем о способах и о том, как расшифровать цифровой код.

Двоичный код

Текстовые данные вполне можно хранить и передавать в двоичном коде. В этом случае по таблице символов (чаще всего ASCII) каждое простое число из предыдущего шага сопоставляется с буквой: 01100001 = 97 = «a», 01100010 = 98 = «b», etc. При этом важно соблюдение регистра.

Расшифруйте следующее сообщение, в котором использована кириллица:

Шифр A1Z26

Это простая подстановка, где каждая буква заменена её порядковым номером в алфавите. Только нижний регистр.

Попробуйте определить, что здесь написано:

Шифрование публичным ключом

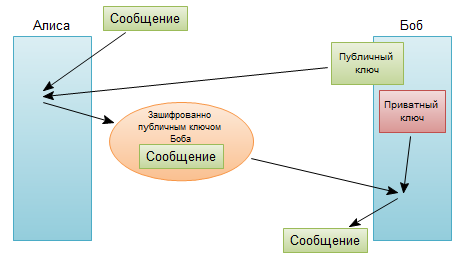
Алгоритм шифрования, применяющийся сегодня буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53.

Открытый ключ используется, чтобы зашифровать сообщение, а секретный — чтобы расшифровать.

Как-то RSA выделила 1000 $ в качестве приза тому, кто найдет два пятидесятизначных делителя числа:

Как расшифровать код или шифр?

Для этого применяются специальные сервисы. Выбор такого инструмента зависит от того, что за код предстоит расшифровать. Примеры шифраторов и дешифраторов:

Источник

Элементарные шифры на понятном языке

Все мы довольно часто слышим такие слова и словосочетания, как «шифрование данных», «секретные шифры», «криптозащита», «шифрование», но далеко не все понимают, о чем конкретно идет речь. В этом посте разберемся, что из себя представляет шифрование и рассмотрим элементарные шифры с тем расчетом, чтобы даже далекие от IT люди поняли суть этого явления.

Прежде всего, разберемся в терминологии.

Шифрование – это такое преобразование исходного сообщения, которое не позволит всяким нехорошим людям прочитать данные, если они это сообщение перехватят. Делается это преобразование по специальным математическим и логическим алгоритмам, некоторые из которых мы рассмотрим ниже.

Исходное сообщение – это, собственно, то, что мы хотим зашифровать. Классический пример — текст.

Шифрованное сообщение – это сообщение, прошедшее процесс шифрования.

Шифр — это сам алгоритм, по которому мы преобразовываем сообщение.

Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.

Алфавит – это перечень всех возможных символов в исходном и зашифрованном сообщении. Включая цифры, знаки препинания, пробелы, отдельно строчные и заглавные буквы и т.д.

Теперь, когда мы говорим на более-менее одном языке, разберем простые шифры.

Шифр Атбаша

Самый-самый простой шифр. Его суть – переворот алфавита с ног на голову.

Например, есть у нас алфавит, который полностью соответствует обычной латинице.

Для реализации шифра Атбаша просто инвертируем его. «А» станет «Z», «B» превратится в «Y» и наоборот. На выходе получим такую картину:

И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра

Исходное сообщение: I love habr
Зашифрованное: r olev szyi

Шифр Цезаря

Тут добавляется еще один параметр — примитивный ключ в виде числа от 1 до 25 (для латиницы). На практике, ключ будет от 4 до 10.

Опять же, для наглядности, возьмем латиницу

И теперь сместим вправо или влево каждую букву на ключевое число значений.

Например, ключ у нас будет 4 и смещение вправо.

Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v

Пробуем написать сообщение:

Шифруем его и получаем следующий несвязный текст:

Шифр Вернама (XOR-шифр)

Простейший шифр на основе бинарной логики, который обладает абсолютной криптографической стойкостью. Без знания ключа, расшифровать его невозможно (доказано Клодом Шенноном).

Исходный алфавит — все та же латиница.

Сообщение разбиваем на отдельные символы и каждый символ представляем в бинарном виде.
Классики криптографии предлагают пятизначный код бодо для каждой буквы. Мы же попробуем изменить этот шифр для кодирования в 8 бит/символ на примере ASCII-таблицы. Каждую букву представим в виде бинарного кода.

Теперь вспомним курс электроники и элемент «Исключающее ИЛИ», также известный как XOR.

XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.

Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.

Теперь для шифровки сообщения, введем сам текст для шифровки и ключ такой же длины. Переведем каждую букву в ее бинарный код и выполним формулу сообщение XOR ключ

сообщение: LONDON
ключ: SYSTEM

Переведем их в бинарный код и выполним XOR:

В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:

С виду — совершенно несвязный набор чисел, но мы-то знаем.

Шифр кодового слова

Принцип шифрования примерно такой же, как у шифра цезаря. Только в этом случае мы сдвигаем алфавит не на определенное число позиций, а на кодовое слово.

Например, возьмем для разнообразия, кириллический алфавит.

Придумаем кодовое слово. Например, «Лукоморье». Выдернем из него все повторяющиеся символы. На выходе получаем слово «Лукомрье».

Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.

И теперь запишем любое сообщение и зашифруем его.

Получим в итоге следующий нечитаемый бред:

Шифр Плейфера

Классический шифр Плейфера предполагает в основе матрицу 5х5, заполненную символами латинского алфавита (i и j пишутся в одну клетку), кодовое слово и дальнейшую манипуляцию над ними.

Пусть кодовое слово у нас будет «HELLO».

Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.

Теперь возьмем любое сообщение. Например, «I LOVE HABR AND GITHUB».

Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.

Если бы сообщение было из нечетного количества символов, или в биграмме были бы два одинаковых символа (LL, например), то на место недостающего или повторившегося символа ставится символ X.

Шифрование выполняется по нескольким несложным правилам:

1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.

Например, EH становится LE.

2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.

Например, если бы у нас была биграмма LX, то она стала бы DL.

3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.

Например, биграмма RA.

По этим правилам, шифруем все сообщение.

Если убрать пробелы, то получим следующее зашифрованное сообщение:

Поздравляю. После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.

Источник

Кодирование и Шифрование

В наш век интернет-технологий, когда мы доверяем все свои данные интернет-сервисам, нужно знать и понимать, как они их хранят и обрабатывают.

Но зачем это вообще нужно знать? Чтобы попросту не попасть в ситуацию, когда ваши личные данные, пароли от аккаунтов или банковских карт окажутся в руках мошенников. Как говорится: «Доверяй, но проверяй»

Важные аспекты в хранении данных, будь то на внешних серверах или домашнем компьютере, – это прежде всего кодирования и шифрование. Но чем они отличаются друг от друга? Давайте разбираться!

Ни для кого не секрет, что компьютер может хранить информацию, но он не может хранить её в привычной для нас форме: мы не сможем просто так написать на флешки реферат, не можем нарисовать на жестком диске картинку так, чтобы её мог распознать компьютер. Для этого информацию нужно преобразовать в язык понятный компьютеру, и именно этот процесс называется кодированием. Когда мы нажимаем на кнопку на клавиатуре мы передаем код символа, который может распознать компьютер, а не сам символ.

Определения и различия

Кодирование – процесс преобразования доступной нам информации в информацию понятную компьютерную.

Шифрование – процесс изменения информации таким образом, чтобы её смогли получить только нужные пользователи.

Шифрование применялось и задолго до создания компьютеров и информатики как таковой. Но зачем? Цели её применения можно было понять из определения, но я опишу их ещё раз более подробно. Главные цели шифрования это:

конфиденциальность – данные скрыты от посторонних

целостность – предотвращение изменения информации

идентифицируемость – возможность определить отправителя данных и невозможность их отправки без отправителя

Оценить стойкость шифра можно с помощью криптографической стойкости.

Криптографическая стойкость – это свойство шифра противостоять криптоанализу, изучению и дешифровки шифра.

Криптостойкость шифра делится на две основные системы: абсолютно стойкие системы и достаточно стойкие системы.

Абсолютно стойкие системы – системы не подверженные криптоанализу. Основные критерии абсолютно стойких систем:

Ключи должны генерироваться для каждого сообщения отдельно

Генерация ключей независима

Длина ключа должна быть не меньше длины сообщения

К сожалению, такие системы не удобны в своём использовании: появляется передача излишней информации, которая требует мощных и сложных устройств. Поэтому на деле применяются достаточно стойкие системы.

Достаточно стойкие системы – системы не могут обеспечить полную защиту данных, но гораздо удобнее абсолютно стойких. Надежность таких систем зависит от возможностей крипто аналитика:

Количества перехваченных сообщений

Времени и вычислительных способностей

А также от вычислительной сложности шифра.

Вычислительная сложность – совокупность времени работы шифрующей функции, объема входных данных и количества используемой памяти. Чем она больше, тем сложнее дешифровать шифр.

История шифрования

Шифрование берет своё начало ещё из древних времен. Примерно 1300 лет до нашей эры был создан один из первых методов шифрования – Атбаш. Принцип шифрования заключается в простой подставке символов по формуле:, где:

n – количество символов в алфавите

i – порядковый номер символа.

Шифр получил своё название в честь первой, последней, второй и предпоследней буквы Еврейского алфавита — «алеф», «тав», «бет», «шин» . Такой шифр имеет низку криптографическую стойкость, потому как алгоритм шифрования довольно прост

С тех самых пор шифрование активно развивалось вместе с развитием нашей цивилизации

Хоть шифры и менялись, но их принцип нет – для расшифровки сообщения требуется ключ. В случае с Абашем ключом может считать последовательность порядковых номеров исходных символов, но этот ключ ещё надо как-то передать. Методы шифрования, которые используются сейчас, научились-таки передавать ключи по открытым и незащищённым каналам связи. Казалось бы, передача ключей шифрования по обычным каналам — это добровольное жертвование своими данными, но не всё так просто. Разберём это на примере популярного алгоритма шифрования «RSA», разработанного в 1977 году.

Первым делом выбирается два случайный простых числа, которые перемножаются друг на друга – именно это и есть открытый ключ.

К слову: Простые числа — это те числа, которые могут делиться без остатка либо на 1, либо на себя.

Длина таких чисел может быть абсолютно любая. К примеру, возьмем два простых числа 223 и 13. Их произведение 2899 – будет являться открытым ключом, который мы и будем передавать по открытому каналу связи. Далее нам необходимо вычислить функцию «Эйлера» для произведения этих чисел.

Функция Эйлера – количество натуральных чисел, меньших чем само число и, которые будут являть взаимно простыми числами с самим числом.

Возможно, звучит непонятно, но давайте это разберем на небольшом примере:

φ (26) [фи от двадцати шести] = какому-то числу чисел, которое всегда будет меньше 26, а сами числа должны иметь только один общий делитель единицу с 26.

1 – подходит всегда, идем дальше;

2 – делится и на 2, и на 1, как и число 26, — не подходит;

3 – делится и на 3, и на 1, а вот число 26 не делится на 3, — подходит;

4 – имеет общие делители 2 и 1 с 26 — не подходит;

5 – только на 1 — подходит;

6 – на 2 и 1 — не подходит;

7 – только на 1 – подходит;

и так далее до 25.

Общее количество таких чисел будет равно 12. А найти это число можно по формуле: φ(n*k) = (n-1)(k-1) в нашем случае 26 можно представить как 2 * 13, тогда получим φ(26) = φ(2 * 13) = (2-1)*(13-1) = 1 * 12 = 12

Теперь, когда мы знаем, что такое функция Эйлера и умеем её вычислять найдем её для нашего открытого ключа – φ(2899) = φ(223 * 13) =(223 – 1)*(13-1) = 222 * 12 = 2664

После чего нам нужно найти открытую экспоненту. Не пугайтесь, тут будет гораздо проще чем с функцией «Эйлера».

Открытая экспонента – это любое простое число, которое не делится на функцию Эйлера. Для примера возьмем 13. 13 не делится нацело на число 2664. Вообще открытую экспоненту лучше выбирать по возрастанию простым перебором, а не просто брать случайную. Так для нашего примера разумнее было бы взять число 5, но давайте рассмотрим на примере 13

Следующий шаг – закрытая экспонента. Вычисляется она банальным перебором по этому равенству: d * e mod φ(n) = 1 , где

φ(n) — функция Эйлера

e – открытая экспонента

mod – остаток отделения

а число d, которое и является закрытой экспонентой, мы должны подобрать перебором, либо попытаться выразить через формулу d = ceil(φ(n) / e) , где ceil – округление в большую сторону.

В обоих случаях у нас получится число 205

На этом подготовка отправки сообщения успешно завершается и начинается самое веселое – отправка данных для дешифрования сообщения. На этом шаге мы отправляем открытый ключ и открытую экспоненту человеку, сообщение которого хотим получить. Предположим, что в этот момент наш ключ и экспоненту перехватили 3-е лица, но до нужного нам человека они всё так же дошли

Теперь этому человеку нужно отправить нам сообщение, для простоты предположим, что это какое-то число, например: 92. Для этого ему нужно отправить нам остаток от деления 92 в степени открытой экспоненты на открытый ключ – T ^ e mod n , где

T – шифруемый текст

e – открытая экспонента

n – открытый ключ

mod – остаток от деления

92 ^ 13 mod 2899 = 235 . Именно число 235 он нам и отправит.

Предположим, что и в этот раз сообщение перехватили, но нам оно всё так же дошло

Для расшифровки сообщения нам необходимо зашифрованное сообщение возвести в степень закрытой экспонентой и вычислить остаток от деления на открытый ключ – C ^ d mod n , где

С – зашифрованный текст

d – закрытая экспонента

n – открытый ключ

mod – остаток от деления

235 ^ 205 mod 2899 = 92.

Вуаля, и мы имеет исходное число. Но, что насчет перехваченных сообщений? У злоумышленника есть сообщение, ключ и экспонента, но как мы помни для дешифровки ему ещё нужна секретная экспонента, она же секретный ключ, но для того, чтобы вычислить её, ему придется разложить исходный ключ 2899 на множители, а сделать это не так уж и просто, особенно когда вместо двух чисел 223 и 13, будут использовать числа длиной несколько десятков символов

Но ничто в мире не идеально, в том числе и этот метод.

Его первый недостаток – это подборка пары чисел для открытого ключа. Нам нужно не просто сгенерировать случайно число, но ещё и проверить на то простое ли оно. На сегодняшний нет методов, которые позволяют делать это сверх быстро.

Второй недостаток – так же связан с генерацией ключа. Как мы с вами помним: «ключи должны генерировать независимо от каких-либо факторов», но именно это правило нарушается, когда мы пытается сгенерировать строго простые числа.

Третий недостаток – подбор и перебор чисел для экспонент.

Четвертый – длина ключей. Чем больше длина, тем медленнее идет процесс декодирования, поэтому разработчики пытаются использовать наименьшие по длиннее ключи и экспоненты. Даже я акцентировал на это внимание, когда говорил, что лучше взять число 5, вместо 13 для открытой экспоненты. Именно из-за этого и происходит большая часть взломов и утечек данных

Но не стоит печалиться, ведь как я и говорил: криптография и шифрование развивается вместе с развитием цивилизации. Поэтому довольно скоро все мы будем шифровать свои данные с помощью Квантового шифрование.

Этот метод основывается на принципе квантовой суперпозиции – элементарная частица может сразу находится в нескольких положениях, иметь разную энергию или разное направление вращения одновременно. По такому принципу и работает передача ключей шифрования по протоколу BB-84.

Есть оптоволокно, по которому передаются единичные фотоны света. Мы, как отправитель может сгенерировать абсолютно любой двоичный ключ, по тому же принципу квантовой супер позиции, ну или использовать обычные генераторы псевдослучайных чисел. Допустим мы хотим передать ключ 101001011. Для этого нам нужно принять за обозначение какое положение фотона соответствует единице, а какое нулю. Представим, что вертикальное положение – это 1, а горизонтальное – 0. Если оставить все так, то от передачи ключей таким образом не будет никакого смысла, ведь тогда злоумышленник всегда сможет измерить фотон, получить его значение, создать и отправить точно такой же обратно человеку, которому мы хоти передать ключ. Поэтому были введены ещё два положение – диагональные. Предоставим вертикальную волну, или же значение 1 и отклоним её на 45 градусов влево. Это будет вторая единица. Вернемся обратно и отклоним на 45 градусов вправо – это будет второй 0.

Вернемся к нашему ключу 101001011. Мы случайным образом выбираем направление – обычное или диагональное. Для удобства присвоим обычному номер 1, а диагональному 2.

Давайте отправим ключ – 1(1), 0(2), 1(1), 0(1), 0(1), 1(2), 0(2), 1(1), 1(2). Теперь человеку, которому мы отправляем ключ, нужно точно так же, совершенно случайно, выбрать случайное направление.

Допустим он выбрал направления: 221111212. Поскольку есть всего 2 плоскости отправки: 1 и 2, они же называются: канонический и диагональный базис, то шанс того, что он выбрал правильные направления 50%.

Если он угадал базис – он получил верное значение, если нет – неверное. Учитывая его направления, он получил: 001000011. Теперь нужно отсеять неправильные значения: можно сделать это обменом базисов по любому, даже не защищенному, каналу связи. После этого у нас обоих останется ключ: 0100011. Теперь с помощью его мы можем передавать и кодировать сообщения по обычному методу шифрования.

А что, если кто-то перехватит отправку кода? Тогда ему придется точно также подбирать случайным образом базисы, что добавит ещё 25% погрешности при получении кода человеку, которому мы изначально и отправили его. Чтобы проверить это, после отсеивания мы, как отправитель, должны проверить сколько процентов кода оказалось не верным. В нашем 1 случае это (9 – 7)/9 * 100% = 22% , если это число будет больше 50%, то мы начнем повторную отправку ключей, до тех пор, пока погрешность не будет меньше 50%

Заключение

Причитав и разобрав эту статью, мы с вами узнали, чем отличается кодирование от шифрования, их историю с будущим, узнали каким должен быть идеальный шифр и немного поговорили про крипто анализ. Уже с этими знаниями, которые были предоставлены в этой статье, можно спокойно идти и делать какую-нибудь систему авторизации или пытаться взломать какой-то сайт, главное не перебарщивать.

Источник