Как определить способ картографической проекции

§ 17. КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ

Виды картографических проекций

Для выбора наивыгоднейшего пути при переходе судна из одного пункта в другой судоводитель пользуется картой.

Картой называют уменьшенное обобщенное изображение земной поверхности на плоскости, выполненное по определенному масштабу и способу.

Так как Земля имеет сферическую форму, ее поверхность невозможно изобразить на плоскости без искажений. Если разрезать любую сферическую поверхность на части (по меридианам) и наложить эти части на плоскость, то изображение этой поверхности на ней получилось бы искаженной и с разрывами. В экваториальной части были бы складки, а у полюсов — разрывы.

Для решения навигационных задач пользуются искаженными, плоскими изображениями земной поверхности — картами, в которых искажения обусловлены и соответствуют определенным математическим законам.

Математически определенные условные способы изображения на плоскости всей или части поверхности шара или эллипсоида вращения с малым сжатием называются картографической проекцией, а принятая при данной картографической проекции система изображения сети меридианов и параллелей — картографической сеткой.

Все существующие картографические проекции могут быть подразделены на классы по двум признакам: по характеру искажений и по способу построения картографической сетки.

По характеру искажений проекции разделяются на равноугольные (или конформные), равновеликие (или эквивалентные) и произвольные.

Равноугольные проекции. На этих проекциях углы не искажаются, т. е. углы на местности между какими-либо направлениями равны углам на карте между теми же направлениями. Бесконечно малые фигуры на карте в силу свойства равноугольности будут подобны тем же фигурам на Земле. Если остров круглой формы в природе, то и на кар- те в равноугольной проекции он изобразится кружком некоторого радиуса. Но линейные же размеры на картах этой проекции будут искажены.

Равновеликие проекции. На этих проекциях сохраняется пропорциональность площадей фигур, т. е. если площадь какого-либо участка на Земле в два раза больше другого, то на проекции изображение первого участка по площади тоже будет в два раза больше изображения второго. Однако в равновеликой проекции не сохраняется подобие фигур. Остров круглой формы будет изображен на проекции в виде равновеликого ему эллипса.

Произвольные проекции. Эти проекции не сохраняют ни подобия фигур, ни равенства площадей, но могут иметь какие-нибудь другие специальные свойства, необходимые для решения на них определенных практических задач. Наибольшее применение в судовождении из карт произвольных проекций получили ортодромические, на которых ортодромии (большие круги шара) изображаются прямыми линиями, а это очень важно при использовании некоторых радионавигационных систем при плавании по дуге большого круга.

Картографическая сетка для каждого класса проекций, в которой изображение меридианов и параллелей имеет наиболее простой вид, называется нормальной сеткой.

По способу построения картографической нормальной сетки все проекции делятся на конические, цилиндрические, азимутальные, условные и др.

Конические проекции. Проектирование координатных линий Земли производят по какому-либо из законов на внутреннюю поверхность описанного или секущего конуса, а затем, разрезав конус по образующей, разворачивают его на плоскость.

Для получения нормальной прямой конической сетки делают так, чтобы ось конуса совпадала с земной осью PNР S (рис, 33). В этом случае меридианы изображаются прямыми линиями, исходящими из одной точки, а параллели — дугами концентрических окружностей. Если ось конуса располагают под углом к земной оси, то такие сетки называют косыми коническими.

В зависимости от закона, выбранного для построения параллелей, конические проекции могут быть равноугольными, равновеликими и произвольными. Конические проекции применяются для географических карт.

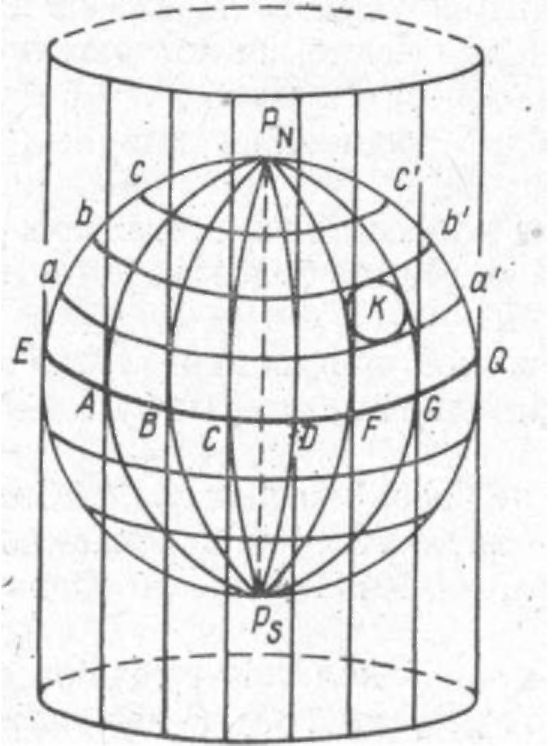
Цилиндрические проекции. Картографическую нормальную сетку получают путем проектирования координатных линий Земли по какому-либо закону на боковую поверхность касательного или секущего цилиндра, ось которого совпадает с осью Земли (рис.34), и последующей развертки по образующей на плоскость.

В прямой нормальной проекции сетка получается из взаимно перпендикулярных прямых линий меридианов Л, В, С, D, F, G и параллелей аа’,bb’,сс При этом без больших искажений будут изображены участки поверхности экваториальных районов (см, окружность К и ее проекцию К на рис. 34), но участки полярных районов в этом случае не могут быть спроектированы.

Если повернуть цилиндр так, чтобы ось его расположилась в плоскости экватора, а поверхность его касалась полюсов, то получается поперечная цилиндрическая проекция (например, поперечная цилиндрическая проекция Гаусса). Если цилиндр поставить под другим углом к оси Земли, то получаются косые картографические сетки. На этих сетках меридианы и параллели изображаются кривыми линиями.

Азимутальные проекции. Нормальную картографическую сетку получают проектированием координатных линий Земли на так называемую картинную плоскость Q (рис. 35) — касательную к полюсу Земли. Меридианы нормальной сетки на проекции имеют вид радиальных прямых, исходящих из. центральной точки проекции P N под угла- ми, равными соответствующим углам в натуре, а параллели — концентрическими окружностями с центром в полюсе. Картинную плоскость можно располагать в любой точке земной поверхности, и точку касания называют центральной точкой проекции и принимают за зенит.

Азимутальная проекция зависит от того, какими радиусами проводятся параллели. Подчиняя радиусы той или иной зависимости от широты, получают различные азимутальные проекции, удовлетворяющие условиям либо равноугольности, либо равновеликости.

Перспективные проекции. Если картографическую сетку получают проектированием меридианов и параллелей на плоскость по законам линейной перспективы из постоянной точки зрения Т.З. (см. рис. 35), то такие проекции называют перспективными. Плоскость можно располагать на любом расстоянии от Земли или так, чтобы она касалась ее. Точка зрения должна находиться на так называемом основном диаметре земного шара или на его продолжении, причем картинная плоскость должна быть перпендикулярна основному диаметру.

Когда основной диаметр проходит через полюс Земли, проекция называется прямой или полярной (см. рис. 35); при совпадении основного диаметра с плоскостью экватора проекция называется поперечной или экваториальной, а при других положениях основного диаметра проекции называются косыми или горизонтальными.

Кроме того, перспективные проекции зависят от расположения точки зрения от центра Земли на основном диаметре. Когда точка зрения совпадает с центром Земли, проекции называются центральными или гномоническими; когда точка зрения находится на поверхности Землистереографическими; при удалении точки зрения на какое-либо известное расстояние от Земли проекции называются внешними, и при удалении точки зрения в бесконечность —ортографическими.

На полярных перспективных проекциях меридианы и параллели изображаются аналогично полярной азимутальной проекции, но расстояния, между параллелями получаются разными и обусловлены положением точки зрения на линии основного диаметра.

На поперечных и косых перспективных проекциях меридианы и параллели изображаются в виде эллипсов, гипербол, окружностей, парабол или прямых линий.

Из особенностей, свойственных перспективным проекциям, следует отметить, что на стереографической проекции любой круг, проведенный на земной поверхности, изображается в виде окружности; на центральной проекции всякий большой круг, проведенный на земной поверхности, изображается в виде прямой линии, в связи с чем в некоторых частных случаях эту проекцию представляется целесообразным применять в навигации.

Условные проекции. К этой категории относятся все проекции, которые по способу построения нельзя отнести ни к одному из перечисленных выше видов проекций. Они обычно удовлетворяют каким-нибудь заранее поставленным условиям, в зависимости от тех целей, для которых требуется карта. Число условных проекций не ограничено.

Небольшие участки земной поверхности до 85 км можно изобразить на плоскости с сохранением на них подобия нанесенных фигур и площадей. Такие плоские изображения небольших участков земной поверхности, на которых искажениями практически можно пренебрегать, называются планами.

Планы обычно составляют без всяких проекций путем непосредственной съемки и на них наносят все подробности снимаемого участка.

Из рассмотренных выше проекций в судовождении в основном применяются: равноугольная, цилиндрическая, азимутальная перспективная, гномоническая и азимутальная перспективная стереографическая.

Масштабы

Масштабом карты называется отношение бесконечно малого элемента линии в данной точке и по данному направлению на карте к соответствующему бесконечно малому элементу линии на местности.

Этот масштаб называется частным масштабом, и каждая точка карты имеет свой, присущий только ей, частный масштаб. На картах, кроме частного, различают еще главный масштаб, являющийся исходной величиной для расчетов размеров карты.

Главным называется масштаб, величина которого сохраняется лишь по определенным линиям и направлениям, в зависимости от характера построения карты. На всех остальных частях одной и той же карты величина масштаба больше или меньше главного, т. е. этим частям карты будут соответствовать свои частные масштабы.

Отношение частного масштаба карты в данной точке по данному направлению к главному называется увеличением масштаба, а разность между увеличением масштаба и единицей — относительным искажением длины. На равноугольной цилиндрической проекции масштаб изменяется при переходе с одной параллели на другую. Параллель, по которой соблюден главный масштаб, называется главной параллелью. По мере удаления от главной параллели в сторону полюса величины частных масштабов на одной и той же карте увеличиваются и, наоборот, по мере удаления от главной параллели в сторону экватора величины частных масштабов уменьшаются.

Если масштаб выражается в виде простой дроби (или отношения), делимое которой — единица, а делитель — число, указывающее, скольким единицам длины на горизонтальной проекции данного участка земной поверхности соответствует одна единица длины на карте, то такой масштаб называется численным или числовым. Например, числовой масштаб 1/100000 (1:100000) означает, что 1 см на карте соответствует 100 000 см на местности.

Для определения длины измеряемых линий пользуются линейным масштабом, показывающим, сколько единиц длины высшего наименования на местности содержится в одной единице длины низшего наименования на карте (плане).

Например, масштаб карты «5 миль в I см» или 10 км в 1 см» и т. п. Это значит, что расстояние в 5 миль (или 10 км) на местности соответствует 1 см на карте (плане).

Линейный масштаб на плане или карте помещают под рамкой в виде прямой, разделенной на несколько делений; начальную точку линейного масштаба обозначают цифрой 0, а затем против каждого или некоторых последующих его делений ставят цифры, показывающие соответствующие этим делениям расстояния на местности.

Переход от числового масштаба к линейному осуществляется простым пересчетом мер длины.

Например, чтобы перейти от числового масштаба 1/100000 к линейному, нужно 100 000 см перевести в километры или мили. 100 000 см = 1 км, или, приближенно, 0,54 мили, следовательно, данная карта составлена в масштабе 1 км в 1 см , или 0,54 мили в 1 см.

Если известен линейный масштаб, например 2 мили в 1 см, то для перехода к числовому необходимо 2 мили перевести в сантиметры и сделать запись в виде дроби с числителем единица: 2 • 1852 • 100 — = 370 400 см, следовательно, числовой масштаб данной карты 1/370400

Источник

Виды картографических проекций и их сущность

Географическими картами человек пользуется с глубокой древности. Первые попытки изобразить поверхность Земли были предприняты еще в Древней Греции такими учеными, как Эратосфен и Гиппарх. Естественно, с тех пор картография как наука далеко продвинулась вперед. Современные карты создаются с помощью съемки со спутников и с использованием компьютерных технологий, что, конечно же, способствует увеличению их точности. И все же, на каждой географической карте присутствуют некоторые искажения относительно натуральных форм, углов или расстояний на земной поверхности. Характер этих искажений, а, следовательно, и точность карты, зависит от видов картографических проекций, использованных при создании конкретной карты.

Понятие картографическая проекция

Разберем подробнее, что такое картографическая проекция и какие их виды применяются в современной картографии.

Картографическая проекция – это изображение поверхности Земли на плоскости. Более глубокое с научной точки зрения определение звучит так: картографическая проекция – это способ отображения точек поверхности Земли на некоторой плоскости, при котором между координатами соответствующих точек отображаемой и отображенной поверхностей устанавливается некоторая аналитическая зависимость.

Как строится картографическая проекция?

Построение любых видов картографических проекций происходит в два этапа.

1. Во-первых, геометрически неправильная поверхность Земли отображается на некоторую математически правильную поверхность, которую называют поверхностью относимости. Для наиболее точного приближения в этом качестве чаще всего используют геоид – геометрическое тело, ограниченное водной поверхностью всех морей и океанов, связанных между собой (уровень моря) и имеющих единую водную массу. В каждой точке поверхности геоида сила тяжести приложена нормально. Однако геоид, как и физическую поверхность планеты, также нельзя выразить единым математическим законом. Поэтому в качестве поверхности относимости вместо геоида принимают эллипсоид вращения, придавая ему максимальное подобие геоиду с помощью степени сжатия и ориентации в теле Земли. Называют это тело земным эллипсоидом или референц-эллипсоидом, причем в разных странах для них принимают различные параметры.
2. Во-вторых, принятая поверхность относимости (референц-эллипсоид) переносится на плоскость с использованием той или иной аналитической зависимости. В итоге получаем плоскую картографическую проекцию земной поверхности.

Искажение проекций

А вы не задумывались, почему на разных картах очертания материков немного различаются? На одних картографических проекциях некоторые части света выглядят больше или меньше относительно каких-либо ориентиров, чем на других. Все дело в искажении, с которым проекции Земли переносятся на плоскую поверхность.

Но почему картографические проекции отображают в искаженном виде? Ответ довольно прост. Сферическую поверхность не представляется возможным развернуть на плоскости, избежав складок или разрывов. Поэтому и изображение с нее нельзя отобразить, избежав искажения.

Методы получения проекций

Изучая картографические проекции, их виды и свойства необходимо упомянуть о методах их построения. Итак, картографические проекции получают, используя два основных метода:

В основе геометрического метода лежат закономерности линейной перспективы. Наша планета условно принимается сферой некоторого радиуса и проецируется на цилиндрическую или коническую поверхность, которая может либо касаться, либо рассекать ее.

Проекции, полученные подобным способом, называются перспективными. В зависимости от положения точки наблюдения относительно поверхности Земли перспективные проекции разделяют на виды:

• гномонические или центральные (когда точка зрения совмещена с центром земной сферы);
• стереографические (в этом случае точка наблюдения расположена на поверхности относимости);
• ортографическая (когда поверхность наблюдается из любой точки, находящейся вне сферы Земли; проекция строится переносом точек сферы с помощью параллельных линий, перпендикулярных к отображающей поверхности).

Аналитический метод построения картографических проекций базируется на математических выражениях, связывающих точки на сфере относимости и плоскости отображения. Такой метод является более универсальным и гибким, позволяя создавать произвольные проекции по заранее заданному характеру искажения.

Виды картографических проекций в географии

Для создания географических карт используют множество видов проекций Земли. Их классифицируют по различным признакам. В России применяется классификация Каврайского, которая использует четыре критерия, определяющих основные виды картографических проекций. В качестве характерных классифицирующих параметров используют:

• характер искажения;
• форму отображения координатных линий нормальной сетки;
• расположение точки полюса в нормальной координатной системе;
• способ применения.

Итак, какие существуют виды картографических проекций согласно данной классификации?

Классификация проекций

Далее представлена классификация видов картографических проекций с примерами, исходя из вышеперечисленных основных критериев.

По характеру искажения

Как упоминалось выше, искажение, в сущности, является неотъемлемым свойством любой проекции Земли. Искажена может быть любая характеристика поверхности: длина, площадь или угол. По типу искажений выделяют:

• Равноугольные или конформные проекции, в которых азимуты и углы переносятся без искажений. Координатная сетка в конформных проекциях является ортогональной. Карты, полученные таким путем, рекомендуется использовать для определения расстояний в любом направлении.
• Равновеликие или эквивалентные проекции, где сохраняется масштаб площадей, который принимается равным единице, т. е. площади отображаются без искажения. Такие карты применяют для сравнения площадей.
• Равнопромежуточные или эквидистантные проекции, при построении которых сохраняется масштаб по одному из основных направлений, который принимается единичным.
• Произвольные проекции, на которых могут присутствовать все разновидности искажений.

По форме отображения координатных линий нормальной сетки

Такая классификация является максимально наглядной и, следовательно, наиболее легкой для восприятия. Отметим, однако, что данный критерий относится только к проекциям, ориентированным нормально к точке наблюдения. Итак, исходя из данного характерного признака, различают следующие виды картографических проекций:

Круговые, где параллели и меридианы представляют окружностями, а экватор и средний меридиан сетки в виде прямых линий. Подобные проекции применяют для изображения поверхности Земли в целом. Примерами круговых проекций могут служить равноугольная проекция Лагранжа, а также произвольная проекция Гринтена.

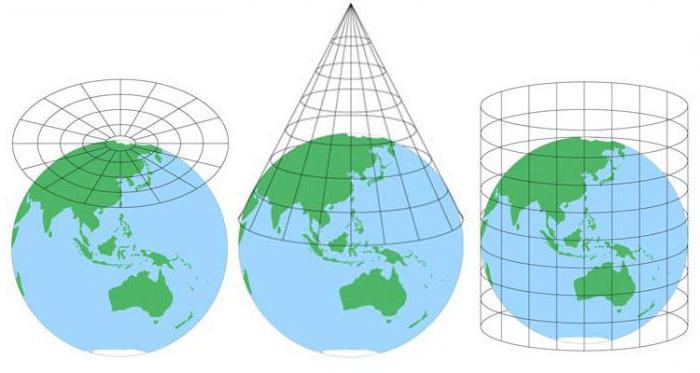
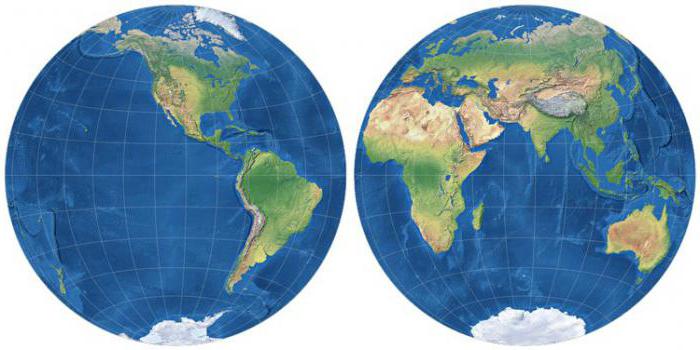
Азимутальные. В данном случае параллели представляют в виде концентрических окружностей, а меридианы в виде пучка расходящихся радиально из центра параллелей прямых. Подобная разновидность проекций используется в прямом положении для отображения полюсов Земли с прилегающими территориями, а в поперечном в качестве знакомой каждому с уроков географии карты западного и восточного полушарий.

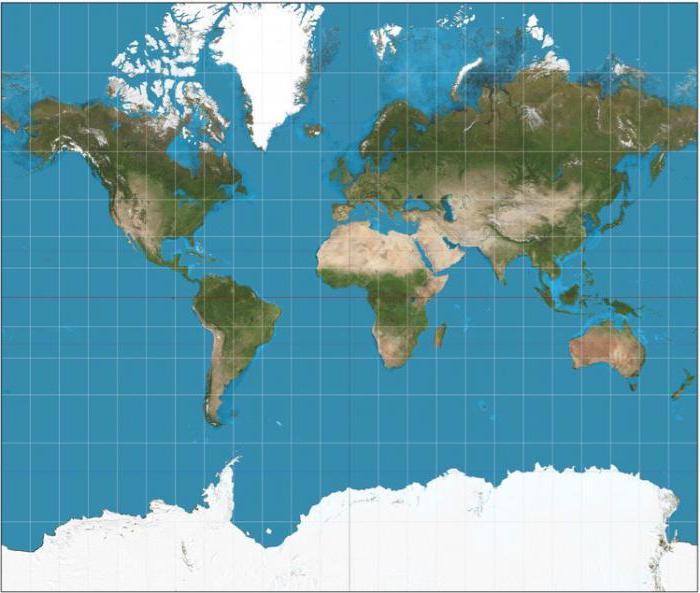
Цилиндрические, где меридианы и параллели представлены прямыми пересекающимися нормально линиями. С минимальным искажением здесь отображаются территории, прилегающие к экватору или же растянутые вдоль некоторой стандартной широты.

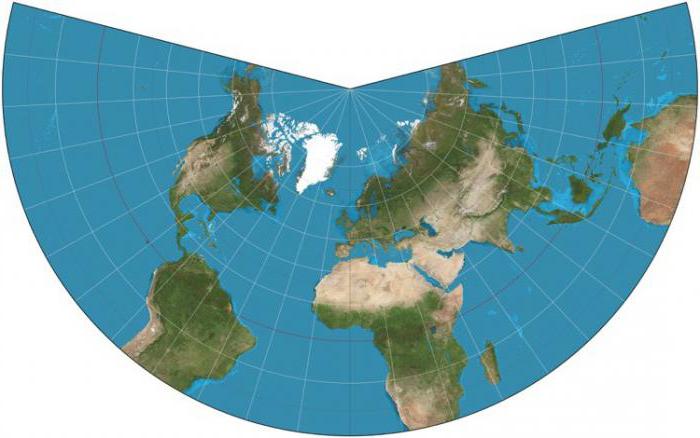
Конические, представляющие собой развертку боковой поверхности конуса, где линии параллелей являются дугами окружностей с центром в вершине конуса, а меридианов – направляющими, расходящимися из вершины конуса. Такие проекции наиболее точно изображают территории, лежащие в средних широтах.

Псевдоконические проекции похожи на конические, только меридианы в данном случае изображаются кривыми линиями, симметричными относительно прямолинейного осевого меридиана сетки.

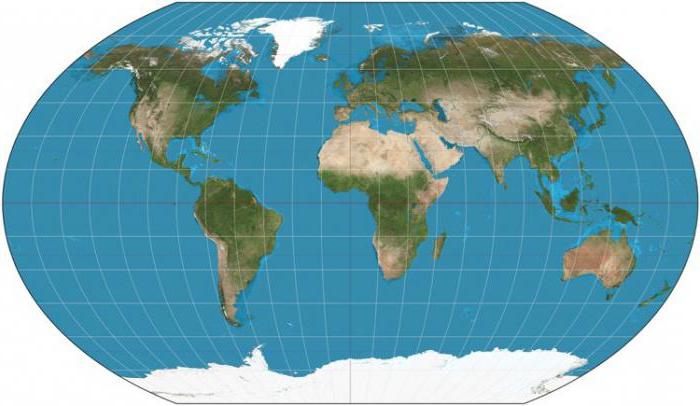
Псевдоцилиндрические проекции напоминают цилиндрические, только, также, как и в псевдоконических, меридианы изображаются кривыми линиями, симметричными осевому прямолинейному меридиану. Используются для изображения Земли целиком (например, эллиптическая проекция Мольвейде, равновеликая синусоидальная Сансона и т. д.).

Поликонические, где параллели изображаются в виде окружностей, центры которых расположены на среднем меридиане сетки или его продолжении, меридианы в виде кривых, расположенных симметрично прямолинейному осевому меридиану.

По положению точки полюса в нормальной системе координат

• Полярные или нормальные – полюс системы координат совпадает с географическим полюсом.
• Поперечные или трансверсионные – полюс нормальной системы совмещается с экватором.
• Косые или наклонные – полюс нормальной сетки координат может находиться в любой точке между экватором и географическим полюсом.

По способу применения

По способу использования выделяют следующие виды картографических проекций:

• Сплошные – проецирование всей территории на плоскость производится по единому закону.
• Многополосные – картографируемая местность условно разбивается на несколько широтных зон, которые проецируют на плоскость отображения по единому закону, но с изменением параметров для каждой зоны. Примером подобной проекции может служить трапециевидная проекция Мюфлинга, которая применялась в СССР для крупномасштабных карт до 1928 г.
• Многогранные – территорию условно разбивают на некоторое количество зон по долготе, проецирование на плоскость производится по единому закону, но с разными параметрами для каждой из зон (например, проекция Гаусса-Крюгера).
• Составные, когда некоторая часть территории отображается на плоскость с использованием одной закономерности, а остальная территория с другой.

Достоинством как многополосных, так и многогранных проекций является высокая точность отображения в пределах каждой зоны. Однако весомым недостатком при этом является невозможность получения сплошного изображения.

Разумеется, каждую картографическую проекцию можно классифицировать с использованием каждого из вышеперечисленных критериев. Так, знаменитая проекция Земли Меркатора является конформной (равноугольной) и поперечной (трансверсионной); проекция Гаусса-Крюгера – конформной поперечной цилиндрической и т. д.

Источник