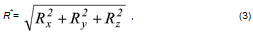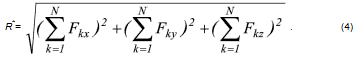Как определить равнодействующую системы сил какими способами

Содержание

iSopromat.ru
Система сходящихся сил
Приведение к равнодействующей
Силовой многоугольник
Вычисление равнодействующей
Техническая механика. Шпаргалка
Оглавление
Техническая механика. Шпаргалка
Оглавление
Пример 1. Определение равнодействующей системы сил

iSopromat.ru

Равнодействующая системы сходящихся сил приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Система сходящихся сил

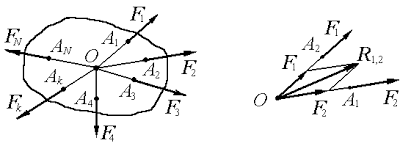
Пусть, к абсолютно твердому телу приложена система N сил (F₁, F₂, … F_N), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).

Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.

Приведение к равнодействующей

Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.

В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О.

Далее, по четвертой аксиоме, силы F₁ и F₂ можно заменить их равнодействующей R_1,2 (рисунок 1), которая определяется диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.

Далее можно записать аналогичные соотношения для полученной равнодействующей силы R * _1,2 и силы F₃, тогда

Для системы N сил окончательно будем иметь

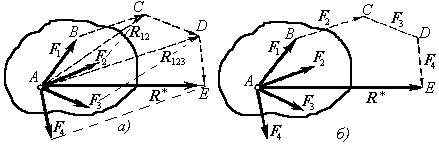
На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника.

Силовой многоугольник

Из конца вектора силы F₁ (точки В) проводим вектор ВС, геометрически равный силе F₂. Из конца этого вектора (точки С) проводим вектор СD равный силе F₃. Из конца этого вектора (точки D) проводим вектор DE, равный силе F₄.

Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами.

Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника.

Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах.

Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.

Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Вычисление равнодействующей

Для аналитического определения равнодействующей найдем ее проекции R_x, R_y, R_z на оси декартовой системы координат. Имеем

Тогда величина равнодействующей определится следующей формулой:

Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:

Здесь α , β , γ — углы между положительным направлением осей координат и равнодействующей.

Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.

В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Техническая механика. Шпаргалка

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

1. Аксиомы и понятие силы статики
2. Связи и реакции связей
3. Определение равнодействующей геометрическим способом
4. Определение равнодействующей аналитическим способом
5. Пара сил. Момент силы

Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

3. Определение равнодействующей геометрическим способом

Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.

Необходимо определить равнодействующую системы сходящихся сил (F₁; F₂; F₃;…; F_n), где n — число сил, входящих в систему.

В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.

Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.

При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.

Многоугольник сил строится в следующем порядке.

1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.

2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).

Задачи решаются в следующем порядке.

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.

Источник

Техническая механика. Шпаргалка

1. Аксиомы и понятие силы статики
2. Связи и реакции связей
3. Определение равнодействующей геометрическим способом
4. Определение равнодействующей аналитическим способом
5. Пара сил. Момент силы

4. Определение равнодействующей аналитическим способом

Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.

Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.

Проекция силы на две взаимно перпендикулярные оси.

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.

Модуль (величину) равнодействующей можно определить по известным проекциям:

Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:

Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской системы сходящихся сил:

При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

Источник

Пример 1. Определение равнодействующей системы сил

Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П 1.1).

Дано: F1 = 10кН; F2 = 15кН; F3 = 12кН; F4 = 8кН; F5 = 8кН;

αl = 30˚; α2 = 60˚; α3= 120˚; α4 = 180˚; α5 = 300˚.

Решение

1. Определить равнодействующую аналитическим способом (рис. П 1.1а).

2. Определить равнодействующую графическим способом.

С помощью транспортира в масштабе 2 мм = 1 кН строим многоугольник сил (рис. П l.l 6). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох.

Результаты расчетов не должны отличаться более чем на 5 %:

Задание № 1

Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способами.

Задание. Используя схему рис. П. 1.1а, определить равнодействующую системы сил.

Параметр	Вариант
F1, кН
F2, кН
F3, кН
F4, кН
F5, кН
1,град	О	О	О	О	О
2,град
3,град	О	О	О	О
4,град
5,град

Параметр	Вариант
F1, кН
F2, кН
F3, кН
F4, кН
F5, кН
1,град	О	О	О	О	О
2,град
3,град	О	О	О
4,град
5,град

Параметр	Вариант
F1, кН
F2, кН
F3, кН
F4, кН
F5, кН
1,град	О	О	О	О
2,град
3,град	О	О	О	О
4,град
5,град

Пример 2. Решение задачи на равновесие аналитическим способом

Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рис. Пl.2).

1. Определяем вероятные направления реакций (рис. П1.2а).

Мысленно убираем стержень АВ, при этом стержень С В опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.

Если убрать стержень СВ, точка В опустится, следовательно, стержень С В поддерживает точку В снизу — реакция направлена вверх.

2. Освобождаем точку В от связи (рис. П1.2б).

3. Выберем направление осей координат, ось Ох совпадает с реакцией Rl.

4. Запишем уравнения равновесия точки В: