Как объяснить способ вычисления

При этом саму запись (9 — 4) тоже можно назвать разностью.

1. Свойство нуля при вычитании
   Если из числа вычесть нуль, получится само число.
   a — 0 = a
   Если из числа вычесть само число, то получится нуль.
   a — a = 0
2. Свойство вычитания суммы из числа
   Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
   a — (b + c) = a — b — c
3. Свойство вычитания числа из суммы
   Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
   (a + b) — c = (a — c) + b (если a > c или а = с)
   (a + b) — c = (b — c) + a (если b > c или b = с)

Примеры использования свойств сложения и вычитания

Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Пример 1

Вычислить сумму слагаемых с использованием разных свойств:

а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15

б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Применить разные свойства при вычислении разности:

а) 25 — 0 — 2 = 25 — 2 = 23

б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13

Пример 3

Найти значение выражения удобным способом:

а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32

б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16

Источник

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок № 57. Разные способы вычислений.

Перечень вопросов, рассматриваемых в теме:

Как выполнять устно вычисления в случаях, сводимых к действиям в пределах 1000, используя различные приёмы устных вычислений?

Как выбирать удобный способ?

Как выполнять проверку вычислений?

Глоссарий по теме:

Круглым называется число, которое делится на 10, 100, 1000 и так далее, без остатка.

Каждая цифра в записи многозначного числа занимает определённое место – позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.

Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
единицы называют единицами 1-го разряда
десятки называют единицами 2-го разряда
сотни называют единицами 3-го разряда и т. д.

Сложение – арифметическое действие в математике, в результате которого два или более чисел объединяется в единое целое, оно обозначается знаком «+». Слагаемое, слагаемое, сумма – главные составляющие математического действия сложения.

Вычитание – арифметическое действие, обратное сложению и обозначается оно знаком «-». Уменьшаемое, вычитаемое, разность- главные составляющие математического действия вычитания.

Основная и дополнительная литература по теме урока:

Моро М.И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 68-69

Волкова С.И. математика. Проверочные работы. 3 кл. — М.: Просвещение, 2018.С. 72-73

Рудницкая В.Н. Математика. Дидактические материалы. Ч.1. 3 кл. – М. «Вентана- Граф», 2016, с. 9-12

Теоретический материал для самостоятельного изучения

Вам уже знакомы приёмы устных вычислений в пределах 1000.

Но наша цель не просто узнать о них, а уверенно ими пользоваться.

Часто ученики допускают ошибки при решении примеров.

Сегодня мы более подробно остановимся на таких случаях и разберемся, как их избежать

Надеюсь, что после урока вы даже сможете посоревноваться с друзьями в устном счёте.

Вспомним приёмы устных вычислений, с которыми познакомились на прошлом уроке.

работаем с разрядными слагаемыми

работаем с общим количеством десятков.

Чтобы быстро и правильно решать такие примеры надо уметь выбирать более удобный способ.

А как выбрать удобный способ?

Выберем из этих примеров те, которые удобнее решать, работая с разрядными слагаемыми.

Согласитесь, что эти примеры будет легко решить, представив одно из слагаемых в виде суммы разрядных слагаемых.

Например: 420 + 50, десятки сложим с десятками и прибавим сотни, а при решении примера 320 + 500 сложим сотни и прибавим десятки.

Что же не так с остальными примерами?

Внимательно посмотри на числа. При выполнении действий с десятками происходит переход через разряд. Это вызывает затруднения.

Именно поэтому здесь удобнее воспользоваться вторым способом – работать с общим количеством десятков.

Рассмотрим первый пример: 150 — 90

Пользуясь первым способом, нам пришлось бы из 50 вычитать 90, а это невозможно.

Приходит на помощь второй способ:

15 дес. — 9 дес. это 6 дес. или 60. Никаких проблем.

Тоже самое с остальными примерами.

Но есть ещё одна опасность при решении подобных примеров на вычитание.

Рассмотрим два примера:

560 — 300 и 600 — 240.

Обрати внимание, в первом примере десятки в уменьшаемом, а во втором — в вычитаемом.

На это очень важно обращать внимание!

Понаблюдаем за решением.

560 — 300 = (500 — 300) + 60 = 260

600 — 240 = (600 — 200) — 40 = 360

В первом случае десятки прибавляем, а во втором вычитаем. Так как в первом случае вычитаем только сотни – 300, а во втором – сотни и десятки — 240

Если же ты сомневаешься в результате или просто хочешь убедиться в правильности, можно выполнить проверку.

Проверка выполняется обратным действием. Сложение проверяем вычитанием и наоборот.

Проверка: 260 + 300 = 560

Проверка: 360 + 240 = 600

Сегодня мы раскрыли вам секреты приёмов устного сложения и вычитания.

Пользуйтесь ими и удачи!

Задания тренировочного модуля:

1. Распределите карточки с примерами на две группы по более удобному способу решения.

1. Поставьте в ячейке напротив «+», если согласны с решением, и «-», если не согласны.

1. Ученик решил примеры. Выберите отметку, которую он получил за работу.

Источник

Как быстро считать в уме: приемы устного счета больших чисел

• 12 января 2021 г.
• 15 минут
• 278 583
• 9

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

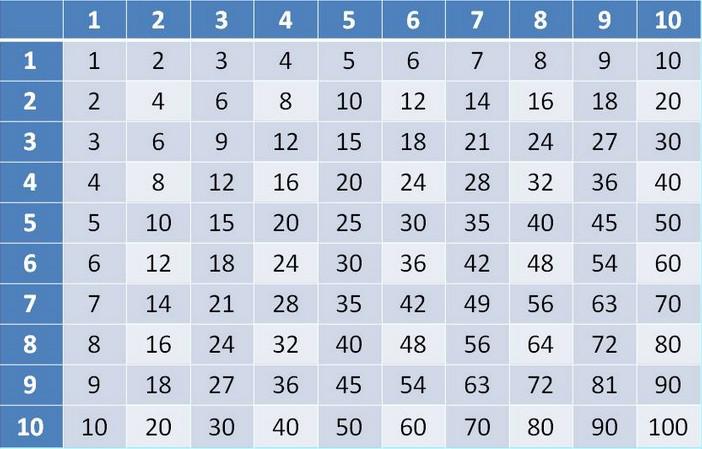
Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник