Как называется способ параллельного проецирования когда проецирующие лучи падают

Чертежик

Метки

Методы проецирования по начертательной геометрии

Методы проецирования заключается в том, что любая точка пространства может быть спроецирована с помощью проецирующих лучей на любую поверхность. Ортогональное проецирование — это такой метод, когда проецирующие лучи параллельны между собой и перпендикулярны к плоскости проекций.

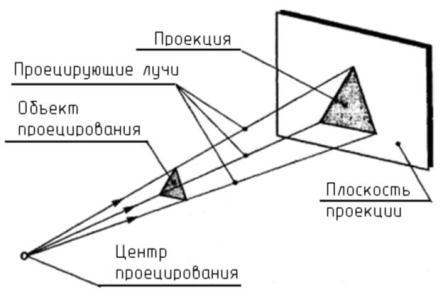
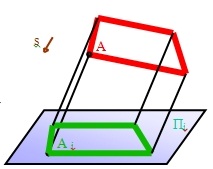
Итак, чтобы получить проекцию какой-либо точки А на плоскость проекций (ее также называют картинной плоскостью) П₀ , необходимо через заданную точку из центра проекций S провести проецирующий луч S_А до пересечения с плоскостью проекций П₀. Полученная точка А₀ называется проекцией точки или изображением точки.

А – геометрический образ.

Пространства;
S – центр проекций;
S_А— проецирующий луч;
А₀ – проекция точки А;

П₀ – плоскость проекций.

В зависимости от положения центра проекций S относительно плоскости проекций П₀, методы проецирования делятся на 2 вида:

Центральное проецирование

В методе центрального проецирования все проецирующие лучи проходят через общую точку S. На рис.2 представлена кривая ℓ точками А, В, С и ее центральная проекция ℓ₁ (А₁, В₁, С₁) на плоскость П₁. Пучок лучей, выходящий из центра S при пересечении с плоскостью проекций П₁, образует коническую поверхность Σ.

Σ ∩ П1 Σ е ℓ. z^> ℓ₁ (А₁, В₁, С1 ) — центральная проекция линии ℓ.

(собственная). А, В, С – произвольные точки, принадлежащие линии ℓ.

S – конечная точка.

Параллельное проецирование

Если центр проекций S – бесконечно удаленная точка, то все проецирующие лучи параллельны между собой. Для проведения этих лучей задается направление проецирования S ∞ .

На рисунке показано построение параллельной проекции кривой ℓ₁ (А₁,В₁,С₁) на плоскость П₁. Параллельные лучи образуют цилиндрическую поверхность Σ.

В свою очередь, параллельное проецирование делится на 2 вида, которые зависят от угла наклона проецирующих лучей к плоскости проекций:

а) прямоугольное или ортогональное проецирование

Каждый из лучей лежит относительно плоскости П₁ под углом 90 0 .

б) косоугольное проецирование

φ — угол наклона проецирующего луча к плоскости проекций П1.

При косоугольном проецировании проецирующие лучи составляют с плоскостью проекций угол, не равный 90° .

Источник

Как называется способ параллельного проецирования когда проецирующие лучи падают

Существует два вида проекций: центральные и параллельные.

Центральное проецирование

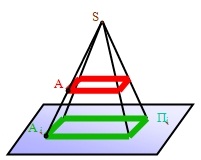
Если все проецирующие лучи проходят через одну и ту же точку, проек­ция называется центральной.

Изображения в центральной проек­ции передают предмет так, как мы его видим. Примером центральной проекции может служить обычная фотография или тень от предмета, освещение лампой.

На flash-ролике за центр проецирования условно взята электрическая лампочка. Исходящие от неё световые лучи, которые условно приняты за про­ецирующие, образуют на полу тень, аналогичную центральной проекции предмета.

Для активации flash-ролика кликните по изображению

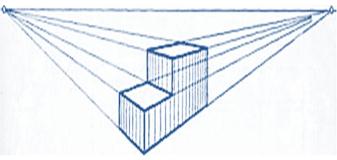
Метод центрального проецирования используется при построении перспективы. Перспектива даёт возможность изображать предметы такими, какими они представляются нам в природе при рассмотрении их с опре­деленной точки наблюдения.

В машиностроительных чертежах центральные проекции не применяются. Ими пользуются в строительном черчении и в рисовании.

Параллельное проецирование

Если все проецирующие лучи параллельны между собой, проек­ция называется параллельной.

В зависимости от угла наклона проецирующего луча к плоскости проекций параллельные проекции делятся на прямоугольные, или ортогональные, и косоугольные. Если проецирующие лучи составляют с плоскостью проекций примой угол, то такие параллельные проекции называются прямоугольными.

На flash-ролике показано, как получается параллельная косоугольная и параллельная прямоугольная проекции. Центр проецирования предполагается условно удалённым в бесконечность. Тогда параллельные лучи отбросят на плоскость проекций тень, которую можно принять за параллельную проекцию изображаемого предмета.

Для активации flash-ролика кликните по изображению

Источник

Основы проецирования

Проецированием называется процесс получения изображения предмета на плоскости.

Получившееся при этом изображение называют проекцией. Проекция – в переводе с латинского – «бросать (отбрасывать) вперёд».

В черчении изображения получают по так называемому методу проекций.

Чтобы построить изображение предмета по методу проекций, нужно через точки на предмете провести воображаемые лучи до встречи их с плоскостью. Эти лучи называются проецирующими. Плоскость, на которой получается изображение предмета, называется плоскостью проекций.

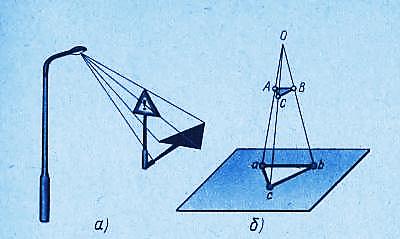
Если проецирующие лучи расходятся из одной точки, проецирование называется центральным (рис. 60а). Точка, из которой выходят лучи, называется центром проецирования.

Полученное при этом изображение называется центральной проекцией. Пример: тени, отброшенные от предмета лучами электрической лампочки.

Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным (рис. 60б), а полученное изображение – параллельной проекцией. Пример: солнечные тени.

При параллельном проецировании все лучи падают на плоскость проекций под одним и тем же углом. Если это любой острый угол, то проецирование называется косоугольным (рис. 61а). В косоугольной проекции, как и в центральной, форма и величина предмета искажаются.

Когда проецирующие лучи перпендикулярны к плоскости проекций, проецирование называют прямоугольным (рис. 61б), а полученное изображение – прямоугольной проекцией.

Способ прямоугольного проецирования является основным в черчении.

Проецирование на одну, две и три взаимно перпендикулярные плоскости проекций

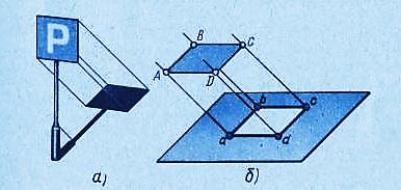
Расположим предмет перед плоскостью проекций так, чтобы на получившемся изображении были видны три его стороны (рис. 62).

По такому изображению легко представить пространственный образ предмета.

Такое проецирование в черчении используют для построения наглядных изображений, однако, на наглядных изображениях предметы получают большие искажения и по ним трудно определить истинные размеры предмета.

Теперь расположим предмет перед плоскостью проекций так, чтобы на изображении была видна только одна его сторона, и построим его прямоугольную проекцию (рис. 63а).

На данном изображении проекции рёбер предмета, которые параллельны двум его измерениям (например: длина и ширина), равны натуральным размерам. Но на таком изображении нет третьего измерения предмета (высоты), поэтому оно не наглядно. Такие изображения используют в случаях, когда высота (толщина) детали одинакова во всех её точках (например, чертежи прокладок). Тогда на чертеже такой детали делают запись, указывающую её толщину (высоту). Пример приведен на рис. 63б (S4).

Иногда на одной плоскости изображают предметы, не имеющие одинаковой высоты во всех его точках. Тогда рядом с изображением точки числом указывают её высоту. Такие изображения называют проекциями с числовыми отметками (рис. 63в).

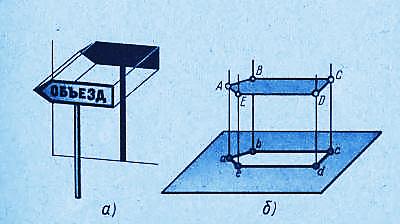
Чтобы судить о трёх измерениях предмета, его необходимо спроецировать ещё на одну плоскость проекций (П₂), которая параллельна другой паре измерений предмета. Тогда вторая плоскость будет расположена перпендикулярно первой плоскости проекций (рис. 64).

Теперь по двум прямоугольным проекциям можно судить о размерах и форме предмета. Хотя форма не всегда ясно выражается двумя проекциями. Поэтому при изображении предметов сложной формы необходимо строить три (а иногда и более) прямоугольных проекции.

Возьмём три взаимно перпендикулярные плоскости проекций (рис. 65).

Одна из них занимает горизонтальное положение, её называют горизонтальной плоскостью проекций и обозначают П₁. Две другие плоскости — вертикальные. Одну называют фронтальной плоскостью проекций (от французского слова «фронталь» – «лицом к зрителю»), другую – профильной плоскостью проекций (от французского слова «профиль» – «вид сбоку») и обозначают соответственно П₂ и П₃.

Линии пересечения плоскостей проекций называют осями проекций и обозначают буквами x, y, z. Точку пересечения осей проекций обозначают буквой О.

В трёхгранный угол, образованный плоскостями проекций, поместим параллелепипед и, проведя проецирующие лучи перпендикулярно плоскостям проекций, получим его проекции. Изображение на плоскости П₁ – горизонтальная проекция, на плоскости П₂ и П₃ – соответственно фронтальная и профильная проекции.

Для получения плоского чертежа трёхгранный угол «разрезают» по оси у, а плоскости П₁ и П 3 поворачивают соответственно вокруг осей х и z по направлению, указанному на рис. 65а стрелками, до совмещения с плоскостью П 2 .

Совмещённые плоскости с построенными на них изображениями предмета показаны на рис. 65б. Линии, соединяющие между собой проекции, называют линиями связи. Линии связи всегда перпендикулярны осям проекций.

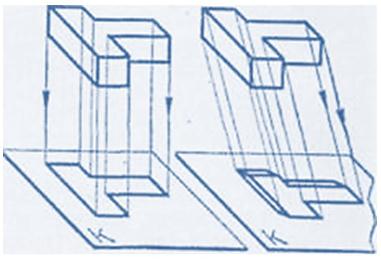
На чертежах плоскости проекций не ограничивают и не обозначают. Кроме того, на чертеже при изображении предмета можно не наносить и оси проекций, так как при параллельном проецировании расстояние от плоскости проекций до изображаемого предмета не влияет на очертание его проекций (рис. 66а).

Это даёт возможность устанавливать произвольное расстояние между проекциями, сохраняя между ними проекционную связь даже при отсутствии линий связи (рис. 66б). Такой чертёж называется безосным. При построении проекций здесь пользуются осями симметрии предмета, центровыми линиями или характерными его плоскостями (рис. 67).

Метод прямоугольного проецирования на две и три взаимно перпендикулярные плоскости был разработан французским учёным-геометром Гаспаром Монжем в конце XVIII века. Поэтому его называют ещё методом Монжа.

Г. Монж положил начало развитию новой науки об изображении предметов – начертательной геометрии.

Способы построения третьей проекции

Проекционную связь между горизонтальной и профильной проекциями можно установить несколькими графическими приёмами:

1. дугой окружности (рис. 68а);
2. с помощью прямой под углом 45° (рис. 68б);
3. с помощью постоянной прямой чертежа (рис. 68в).

На рис. 68а,б,в эти приёмы показаны на примере построения третьей проекции точки.

Удобнее всего пользоваться третьим способом, т.к. при наименьшем количестве графических операций достигается большая точность построения.

Если три вида уже построены, то место постоянной прямой чертежа произвольно выбирать нельзя. Нужно найти точку, через которую она пройдет. Для этого достаточно продолжить до взаимного пересечения горизонтальную и профильную проекции оси симметрии предмета. Через полученную точку К под углом 45° проводят отрезок прямой. Если осей симметрии на чертеже нет, то продолжают до пересечения в точке К₁ горизонтальную и профильную проекции любой грани, проецирующейся в виде отрезков прямой (рис. 69).

Источник

Как называется способ параллельного проецирования когда проецирующие лучи падают

Раздел 2: Проецирование (6 часов)

Понятие о проецировании. Способы проецирования. Центральное и параллельное проецирование. Прямоугольное (ортогональное) проецирование. Проецирование на 2 и 3 взаимно перпендикулярные плоскости. Метод Монжа. Плоскости проекций. Расположение видов. Аксонометрические проекции. Прямоугольная изометрическая проекция. Способы построения прямоугольной изометрической проекции плоских и объемных фигур. Рациональные построения в изометрии. Технический рисунок. Эскиз. Решение творческих задач.

Урок № 5: Понятие о проецировании. Способы проецирования.

Ботвинников А.Д. § 3, 4 [1]

Степакова В. В. § 12, 13 [3]
Вышнепольский И.С. § 16 [8]

pdf Презентация «Способы проецирования»

pdf

Изображения на чертеже выполняют по правилам проецирования. Проецированием называется процесс получения изображения предмета на плоскости – бумаге, экране, классной доске и т. д. Получившееся при этом изображение называют проекцией .

« Проекция» — слово латинское. В переводе на русский язык оно означает « бросать (отбрасывать) вперед».

В основе правил построения изображений на чертеже лежит метод проекций. Метод проекций — отображение геометрической фигуры на плоскость путем проецирования ее (фигуры) точек.

Чтобы построить изображение предмета по методу проекций, необходимо через точки на предмете (например, через его вершины) провести воображаемые лучи до встречи их с плоскостью. Лучи, которые проецируют предмет на плоскость, называются проецирующими .

Плоскость, на которой получается изображение предмета, называется плоскостью проекции .

Рис. 1. Понятия проецирования.

Способы изображения предметов отличаются друг от друга, как методами проецирования, так и условиями их построения. Одни способы дают более наглядное изображение, нетрудны для построения, другие менее наглядны, но зато более просты для построения.

Чтобы выяснить, что представляет собой метод проекций, обратимся к примерам.

Поместим перед электрической лампочкой какой-нибудь предмет. Тень, полученную на стене, можно принять за проекцию предмета. Положите на бумагу какой-нибудь плоский предмет и обведите его карандашом. Вы получите изображение, соответствующее проекции этого предмета.

Посмотрим процесс получения проекций геометрических фигур, из которых состоят дорожные знаки (рис. 2, 5, 8). Для построения изображений этих геометрических фигур использован метод проекций.

На рисунке 2,б проекцией точки А будет точка а, т.е. точка пересечения проецирующего луча Оа с плоскостью проекций. Проекцией точки В будет точка b и т. д. Если теперь соединить на плоскости эти точки прямыми линиями, то мы получим проекцию изображаемой фигуры, например треугольника.

Рис. 2 . Центральное проецирование

На изображениях точки в натуре, т е точки на предмете, будем обозначать большими ( прописными) буквами латинского алфавита. Проекции этих точек на плоскость обозначают теми же, но малыми ( строчными) буквами.

Рассмотренный пример построения изображений составляют сущность метода проекций.

Если проецирующие лучи, с помощью которых строится изображение предмета, расходятся из одной точки, проецирование называется центральным (рис. 2). Точка, из которой выходят лучи ( О), называется центром проецирования. Полученное при этом изображение предмета называется центральной проекцией .

Рис. 3. Центральное проецирование на плоскости.

Величина проекции зависит от положения предмета по отношению к картинной плоскости, а также от расстояния его до этой плоскости и до центра проецирования. На рис. 3, а предмет расположен между центром О и картинной плоскостью К и поэтому его изображение получается увеличенным. Если предмет расположить за плоскостью К (рис. 3, б), то изображение получится уменьшенным.

Центральные проекции часто называют перспективой. Взаимно параллельные линии предмета, не параллельные картинной плоскости, проецируются как группа линий, сходящихся в одной точке (рис. 4).

Рис. 4. Перспектива

Проекции каждой группы параллельных линий имеют свою точку схода О 1 и О 2 . Точки схода проекций всех групп параллельных линий расположены на одной прямой, называемой линией горизонта. Предмет, изображенный на рис. 4, расположен по отношению к картинной плоскости так, что ни одна из его граней не параллельна этой плоскости. Такую центральную проекцию называют угловой перспективой.

Изображение, полученное методом центрального проецирования, сходно с фотографией, так как оно получается примерно таким, каким его видит глаз человека. Также примерами центральной проекции являются кинокадры, тени, отброшенные от предмета лучами электрической лампочки, и др. Метод центрального проецирования используется в архитектуре, строительстве, а также в академическом рисовании – рисовании с натуры.

Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным , а полученное изображение – параллельной проекцией . Примером параллельной проекции являются солнечные тени (рис. 5, 8).

Рис. 5. Параллельное проецирование

При параллельном проецировании все лучи падают на плоскость проекций под одним и тем же углом.

Если это любой угол, отличный от прямого, то проецирование называется косоугольным (рис. 6). В косоугольной проекции, как и в центральной, форма и величина предмета искажаются. Однако строить предмет в параллельной косоугольной проекции проще, чем в центральной.

Рис. 6. Параллельное косоугольное проецирование на плоскости.

В техническом черчении такие проекции используют для построения наглядных изображений (рис.7).

Рис. 7. Процесс поучения наглядного изображения.

В том случае, когда проецирующие лучи перпендикулярны к плоскости проекций (рис. 8), т. ё. составляют с ней угол в 90°. проецирование называют прямоугольным . Полученное при этом изображение называется прямоугольной проекцией предмета.

Рис. 8. Параллельное прямоугольное проецирование.

Проекционное черчение имеет большое значение для развития пространственного представления, без которого невозможно сознательно читать чертежи и тем более выполнять их (рис 9).

Прямоугольные проекции называют также ортогональными . Слово » ортогональный» происходит от греческих слов » orthos» — прямой и » gonia» — угол.

Рис. 9. Параллельное прямоугольное проецирование на плоскости

Способ прямоугольного проецирования является основным в черчении. Он используется для построения изображений на чертежах и наглядных изображений предметов, так как они достаточно наглядны и выполнять их проще, чем центральные.

Чертежи в системе прямоугольных проекций дают достаточно полные сведения о форме и размерах предмета, так как предмет изображается с нескольких сторон.

Практические задания, тесты и домашние работы

Вопросы для повторения

pdf Вопросы

ts2

Источник

Предыдущий урок	Поурочное планирование	Следующий урок